软件工程实践2017第二次作业
解题思路
作业刚发布时,简单听舍友说了下题目大意,当下以为题目是解数独,花了一天时间头脑风暴如何解数独,最后还是没有过优的算法,只得选择最开始想的——回溯法
令人意外的是,等自己看完题目之后,才明白是生成数独。那么最开始的想法自然也是回溯法了,想法分别从行回溯,列回溯,再到块回溯,同时一个有效的数独把1-9各个数字进行替换又能生成9!=362,880个新数独,但是回溯法生成的效率不高以外,将生成的数独中的数字进行全排列又必须要避免出现与之前重复的结果,只能将前面的X回溯法作为备选。但之后想到如果先定下来一个数字的分布,如下图
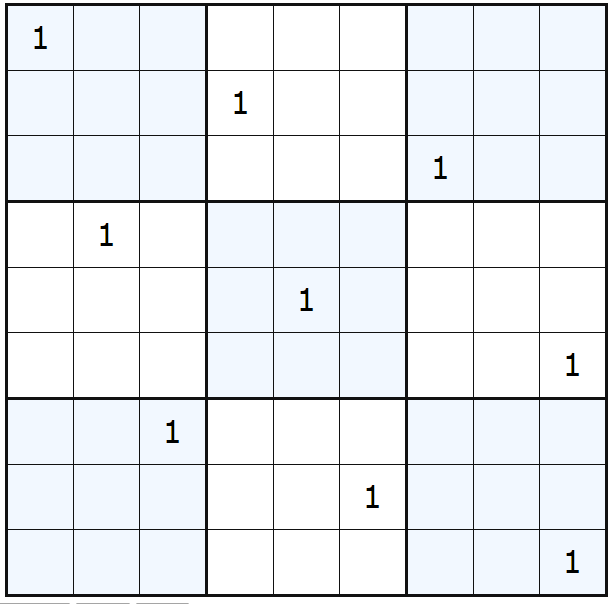
那么决定其余8个数字位置时,难度会更有所降低。同理,定下来两个时,剩余7个数字则更加容易,......,暂且就叫这个方法为格回溯
但格回溯只是决定某个数字的具体位置分布,那么如果将各个数字改成像下图这样的色块呢?

每个色块都可以填入1-9个数字,这样的一副图可以生成9!=362,880种不同的新数独
同时这样的一副图是由像这样的8组小图组成
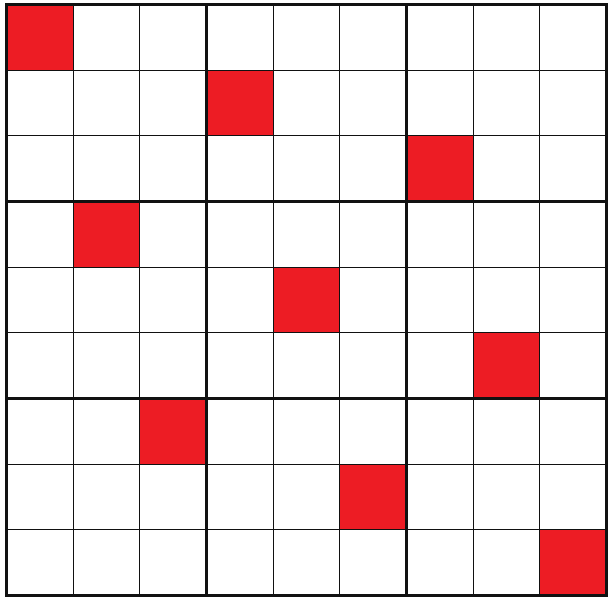
我们只需要找到足够的图,就能够满足题目的100w个不重复数独的要求。但是如何得到这些图又是一个问题?
既然回溯效率太低,想着能不能通过矩阵变化,从一个九宫格扩展成一个数独。这时舍友分享了一篇快速生成数独的链接,甚是贴合我的需要!做法如下:
- 将中心九宫格填入相应内容
- 构造转换规则(
如:当要填充的九宫格在中心左边时,进行横向逆旋转,右边则为横向顺旋转,在中心上方时纵向逆旋转,下方则为纵向顺旋转),来填充四周的九宫格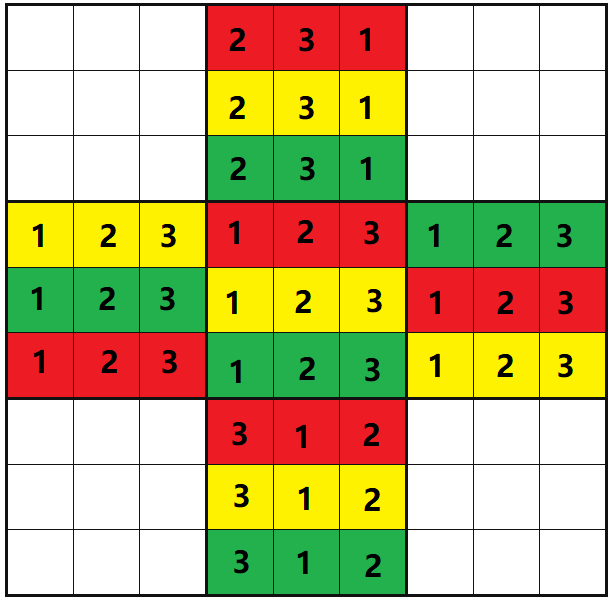
- 再由四个新填充的九宫格,用相同的规则扩展四个边角的九宫格,即可
上述做法的一个转换规则可以快速生成一副填充图,而通过构造转换规则,一共可以得到4副完全不同的填充图。
我们的目标是100w个数独,每个数独左上角固定为(学号后两位相加)% 9 + 1,则一幅填充图能生成8!=40,320个完全不同的数独,这只需要25个以上的填充图就能实现它。
以上面生成的四副图作为基础,将横向的一排九宫格进行一次正/逆旋转分别能得到一个新的图,那么三排就可以获得3*2=6个图,四幅基图则一共得到新的24副新图,合起来就是28副填充图,足够生成100w个完全不同的矩阵了。
随机生成方面,首先利用next_permutation函数枚举色块和数字的映射关系,再随机抽取一副图为起点,通过映射关系来解析,直到图用尽便重复本操作。
设计实现
MapCluster类:生成上文的28副填充图,提供渲染函数,用于把关系映射成一副完整的数独
SudokuNext函数:通过next_permutation枚举全排列,并随机轮转MapCluster的图,返回渲染后的数独
main函数:从命令行读取-c参数后,循环调用SudokuNext并输出到文件中

代码说明
MapConditionGenerate用于生成4副基础图,思路在上面已经讲的很清楚了
void MapCluster::MapConditionGenerate(int map[9][9], int row, int col)
{
// baseMap是中间的九宫格
int baseMap[][3] = { { 1,2,3 },{ 4,5,6 },{ 7,8,9 } };
//tmpX是在横向上的转换规则,tmpY则是纵向上的
int tmX[3] = { row,0,-row }, tmY[3] = { col,0,-col };
//生成9*9的图
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
//这一步是最关键也最复杂的一步,根据转换规则把结果写入9*9的数独中
map[i][j] = baseMap[(3 + i + tmX[j / 3]) % 3][(3 + j + tmY[i / 3]) % 3];
}
}
}
在编码过程中遇到的问题:
- 生成4副基础图时,弄清楚99的矩阵与33九宫格的对应关系十分重要,一开始代码写错了,基础图生成错误,之后找了很久才找到原因
- 使用宏定义时,要注意变量名的正误,我一开始写的宏
#define REPEAT(x,n) for(int i=0;i<n;i++),这里有个很大的错误就是x、i,但是在编译的时候由于提前声明了i变量,编译器没有报错,导致扩展的24副填充图是错误的,生成的数独不是合法数独
测试运行
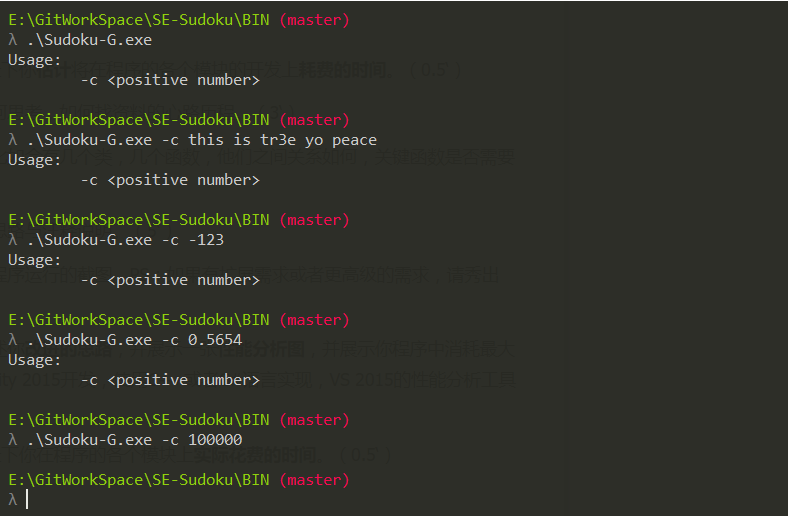
这个算法效率是优秀的,但是少了很多游戏该有的趣味,如果作为游戏的生成算法来说是不可取的,但是在本次作业中并没有相关要求,所以还是相对比较符合题意的
n=100W
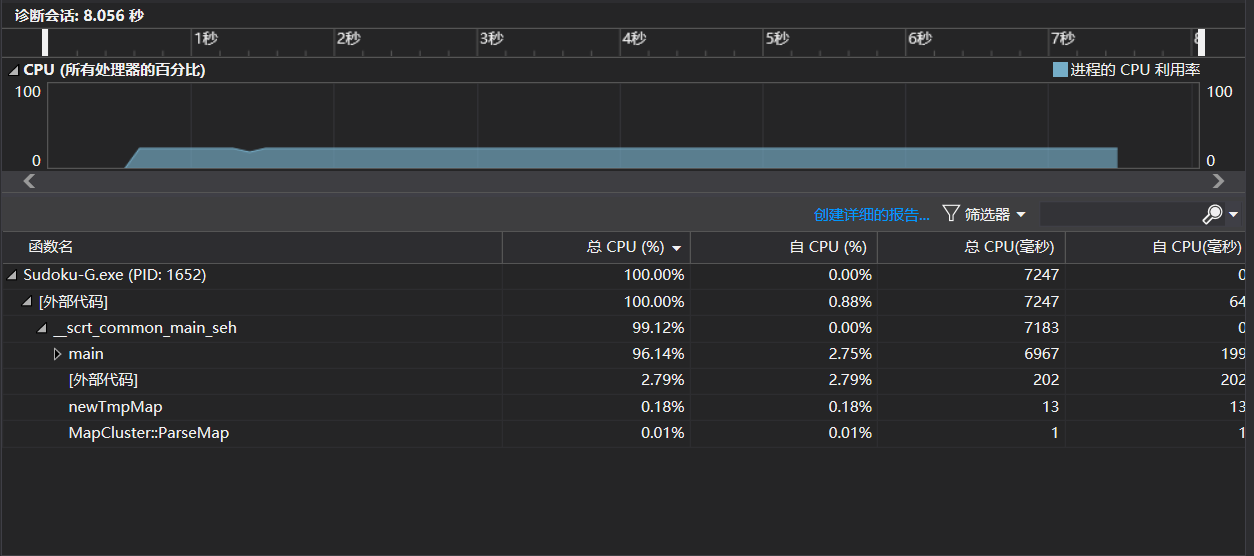

性能瓶颈在于文件的IO操作,一开始使用的是fstream,100W的输出大概需要12.x秒,之后分别尝试了fprintf,fwrite,fputc,其中fputc仅输出1个字符,从简单的逻辑上判断应该是最快的,同时在本机环境中测试的效率最高,时间范围稳定在7.x-8.x秒。
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 15 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 15 |
| Development | 开发 | 780 | 1290 |
| · Analysis | · 需求分析 (包括学习新技术) | 300 | 600 |
| · Design Spec | · 生成设计文档 | 60 | 60 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 0 | 0 |
| · Design | · 具体设计 | 120 | 180 |
| · Coding | · 具体编码 | 240 | 300 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 30 | 120 |
| Reporting | 报告 | 270 | 270 |
| · Test Report | · 测试报告 | 120 | 120 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 120 | 120 |
| 合计 | 1070 | 1575 |


