Cryptanalysis of RSA Variants with Primes Sharing Most Significant Bits

概论

当RSA的公钥e和私钥d满足公式\(ed-k(p^2-1)(q^2-1)=1\)，如果模数m的两个因子p,q有相同的MSB，也就是说，如果p,q的差值\(|p-q|\)比较小，那么就可以计算出上式中的d，并且分解模数m。

RSA变式

RSA-LUC

1993年，Smith 和 Lennon 发表了一个RSA变种密码系统，叫做LUC，基于 Lucas sequences。模数\(N=pq\)，公钥e和私钥d满足 \(ed\equiv1 \pmod{(p^2-1)(q^2-1)}\)。

还有很多其他的变式可以看原文，这些变式都满足 \(ed\equiv1 \pmod{(p^2-1)(q^2-1)}\) 这条式子。

后面的研究中，把这条式子改写为等式 \(ed-k(p^2-1)(q^2-1)=1\) ，并得出 \(\frac{k}{d}\) 可以用 \(e/(N^2-\frac{9}{4}N+1)\)的 连分数形式的逼近来表示，如果 \(d < \sqrt{(2N^3-18N^2)/e}\)，这个方法将非常有效。

在2017年，Bunder发现当公钥e满足 \(ex-(p^2-1)(q^2-1)y=z\)，可以将Coppersmith方法和连分数方法结合起来，如果 \(xy < 2N-4\sqrt{2}N^{\frac{3}{4}}\) 且 \(|z| < |p-q|N^{\frac{1}{4}}y\) ，那么可以很有效的分解N，当z=1时，上式变为 \(ed-k(p^2-1)(q^2-1)=1\) ，d 的上界为 \(d < \sqrt{2N-4\sqrt{2}N^{\frac{3}{4}}}\) 。d 和 e 的界也被考虑成 \(e = N^{\alpha}\) 和 \(d = N^{\delta}\) 。再到后来密码学家们发现 \(ed\equiv1 \pmod{(p^2-1)(q^2-1)}\) 可以被解决，如果 \(\delta < \frac{7}{3} - \frac{2}{3}\sqrt{1+3\alpha}\) 。

这篇论文主要论述的是RSA模数N=pq，且 \(q < p < 2q\)，\(p-q=N^{\beta}\)。如果p和q满足 \(q<p<2q\)，那么 \(\beta\) 总是小于0.5的，而且当 \(\beta\) 小于0.25时就可以费马分解的方法直接分解N了。

连分数方法攻击

定理 令 \(N=pq\) 是 RSA 的模数，\(q<p<2q\)，\(|p-q|=N^{\beta}\) 。令加密指数 \(e=N^{\alpha}\) 满足 \(ed-k(p^2-1)(q^2-1)=1\) 。如果

\[\delta < 2-\beta - \frac{1}{2}\alpha \]

可以再多项式时间内找到p，q 。

证明

\[\begin{aligned} e d-(N-1)^{2} k & =k\left(p^{2}-1\right)\left(q^{2}-1\right)+1-(N-1)^{2} k \\ & =1+k\left(\left(p^{2}-1\right)\left(q^{2}-1\right)-(N-1)^{2}\right) \\ & =1-k(p-q)^{2} \end{aligned} \]

由此推出

\[\left|\frac{e}{(N-1)^{2}}-\frac{k}{d}\right|=\frac{\left|1-k(p-q)^{2}\right|}{d(N-1)^{2}}<\frac{k(p-q)^{2}}{d(N-1)^{2}} . \]

由e, d 的关系，得到 \(k(p^2-1)(q^2-1)=ed-1<ed\) ，所以

\[\frac{k}{d}<\frac{e}{\left(p^{2}-1\right)\left(q^{2}-1\right)}, \]

和

\[\left|\frac{e}{(N-1)^{2}}-\frac{k}{d}\right|<\frac{e(p-q)^{2}}{(N-1)^{2}\left(p^{2}-1\right)\left(q^{2}-1\right)} \]

因为 \(q<p<2q\) 所以

\[N^2-\frac{5}{2}N+1<(p^2-1)(q^2-1)<N^2-2N+1 \]

然后得到

\[\begin{aligned} (N-1)^{2}\left(p^{2}-1\right)\left(q^{2}-1\right) & >(N-1)^{2}\left(N^{2}-\frac{5}{2} N+1\right) \\ & =N^{4}-\frac{9}{2} N^{3}+7 N^{2}-\frac{9}{2} N+1 \\ & >\frac{1}{2} N^{4}, \end{aligned} \]

这个不等式要求 \(N\ge8\) 。因此用 \(e=N^{\alpha}\) ，\(|p-q|=N^{\beta}\) 以及 \(d=N^{\delta}\) ，我们得到

\[\left|\frac{e}{(N-1)^{2}}-\frac{k}{d}\right|<\frac{e(p-q)^{2}}{(N-1)^{2}\left(p^{2}-1\right)\left(q^{2}-1\right)}<2 N^{\alpha+2 \beta-4} . \]

如果 \(2N^{\alpha+2\beta-4}<\frac{1}{2}N^{-2\delta}\) ，由于指数的作用比乘积大，也就是说前面的不等式等价于 \(\delta<2-\beta-\frac{1}{2} \alpha\) 。

那么就有

\[\left|\frac{e}{(N-1)^{2}}-\frac{k}{d}\right|<\frac{1}{2} N^{-2 \delta}=\frac{1}{2 d^{2}} \]

由于 d 是一个很大的数，所以 \(1/2d^2\) 非常小，就能知道 \(\frac{k}{d}\) 和 \(\frac{e}{(N-1)^2}\) 非常接近，于是就可以用\(\frac{e}{(N-1)^2}\) 的连分数去逼近 \(\frac{k}{d}\) ，然后用\(ed-k(p^2-1)(q^2-1)=1\) 和 \(N=pq\) 去解 p 和 q 。

总的来看和 Wiener's Theorem 还是很相似的，e, d 的关系变成 \(ed-k(p^2-1)(q^2-1)=1\) ，在公式的推导中利用的很多不等式和近似。

简单总结一下：

• 连分数攻击适用于 \(\delta<2-\beta-\frac{1}{2} \alpha\) ，其中 \(d=N^{\delta}\) ， \(e=N^{\alpha}\) ，\(|p-q|=N^{\beta}\) 。也就是 \(d^2 < N^4-|p-q|^2-e\) 如果粗糙一点说也可以用这个不等式来判断 \(d < \sqrt{(2N^3-18N^2)/e}\) 。
• 找 \(\frac{e}{(N-1)^2}\) 的连分数逼近
• 迭代 \(\frac{k_i}{d_i}\) 利用 e, d 关系 \(ed-k(p^2-1)(q^2-1)=1\) 和 \(N=pq\) 去分解N。

demo

attack function by sagemath

# contiune fraction method
def attack(N, e):
    """
    Recovers the prime factors of a modulus and the private exponent if two prime factors share most significant bits
    :param N: the modulus
    :param e: the public exponent
    :return: a tuple containing the prime factors and the private exponent, or None if the private exponent was not found
    """
    PR = PolynomialRing(ZZ, 'x')
    x = PR.gen()
    convergents = continued_fraction(ZZ(e) / ZZ((N-1)**2)).convergents()
    for c in convergents:
        k = c.numerator()
        d = c.denominator()
        try:
            f = x**2 - x*(N**2 + 1 - int((e*d-1)/k)) + N**2
            if f.discriminant() > 0:
                root = f.roots()
                p2 = root[0][0]; q2 = root[1][0]
                if is_square(p2) and is_square(q2):
                    p = isqrt(p2); q = isqrt(q2)
                    if p*q == N:
                        return p, q, d
        except:
            continue
    return None

测试代码

from sage.all import *
from math import isqrt

# genetare parmater 
n_bits = 1024
p = random_prime(2**512, lbound=2**511)
beta = 0.46
pqdiff_bound = 1 << int(n_bits * beta)
pqdiff_lower_bound = 1 << int(n_bits * beta - 1)
q = next_prime(p - random_prime(pqdiff_bound, lbound=pqdiff_lower_bound))
assert p > q and p < 2*q
N = p*q
phi = (p**2-1)*(q**2-1)
delta = 0.54
d_bound = 1 << int(n_bits*delta)
d_lower_bound = 1 << int(n_bits * delta - 1)
while True:
    d = random_prime(d_bound, lbound=d_lower_bound)
    if gcd(d, phi) == 1:
        e = inverse_mod(d, phi)
        if gcd(e, phi) == 1:
            alpha = int(e).bit_length() / n_bits
            break
# paramters
print(f"alpha = {alpha}")
print(f"beta = {beta}")
print(f"delta = {delta}")
print(f"p = {p}")
print(f"q = {q}")
print(f"e = {e}")
print(f"d = {d}")
# check
attack_bound = ZZ(isqrt((2*N**3 - 18*N**2)//ZZ(e)))
print(f"check step 1: {d < attack_bound}")
print(f"check step 2: {delta < 2-beta-0.5*alpha}")
# contiune fraction method
def attack(N, e):
    """
    Recovers the prime factors of a modulus and the private exponent if two prime factors share most significant bits
    :param N: the modulus
    :param e: the public exponent
    :return: a tuple containing the prime factors and the private exponent, or None if the private exponent was not found
    """
    PR = PolynomialRing(ZZ, 'x')
    x = PR.gen()
    convergents = continued_fraction(ZZ(e) / ZZ((N-1)**2)).convergents()
    for c in convergents:
        k = c.numerator()
        d = c.denominator()
        try:
            f = x**2 - x*(N**2 + 1 - int((e*d-1)/k)) + N**2
            if f.discriminant() > 0:
                root = f.roots()
                p2 = root[0][0]; q2 = root[1][0]
                if is_square(p2) and is_square(q2):
                    p = isqrt(p2); q = isqrt(q2)
                    if p*q == N:
                        return p, q, d
        except:
            continue
    return None

result = attack(N, e)
assert result != None, "no result"
p, q, d = result
print("attack finish, get")
print(f"p = {p}")
print(f"q = {q}")
print(f"d = {d}")

输出

alpha = 1.99609375
beta = 0.46
delta = 0.54
p = 8406643377981629626811646133771198403255255522467207444991622697680850682941538832110654789948650168347547487883409896215504739533322889924095611950833997
q = 8406643377977179979671041238653918211315952818096881317941557663045423915326379167410018138334335185395189383254205899373386216155386760699272210407922759
e = 1110800340083303328409168504484065292940668235722045412659413083991459540716589704385849056470951835369439790243586123952050852123679997511675601108424970995223757885717140402024028525018368572164542875329515620447453397899075007131099258157788275439784354313980338033207127998650481283926225741172740750647416454068540786594711130891562928160432618419846698928632055429541344493485659153805653186418897286561907086377175044409847334727768680508645477651906431561168347733901347223084949905765613688938377277010995416972766098844482178898448679408222490011796397878275175763710131617180329057114830701572732576610783
d = 13874613842901198703840384827215457417464863664524770654955846214097908890393956737749090737131189322336619851723197432511838668534730694642961386947340470001867225887
check step 1: False
check step 2: True
attack finish, get
p = 8406643377981629626811646133771198403255255522467207444991622697680850682941538832110654789948650168347547487883409896215504739533322889924095611950833997
q = 8406643377977179979671041238653918211315952818096881317941557663045423915326379167410018138334335185395189383254205899373386216155386760699272210407922759
d = 13874613842901198703840384827215457417464863664524770654955846214097908890393956737749090737131189322336619851723197432511838668534730694642961386947340470001867225887

测试过来上面的参数已经挺极限的了，再往上调解不出来的可能性很大。

Coppersmith 方法攻击

定理 令 \(N=pq\) 是 RSA 的模数，\(q<p<2q\)，\(|p-q|=N^{\beta}\) 。令加密指数 \(e=N^{\alpha}\) 满足 \(ed-k(p^2-1)(q^2-1)=1\) ， \(d=N^{\delta}\) 。如果

\[\delta < 2-\sqrt{2\alpha\beta}-\epsilon \]

对于小的正数 \(\epsilon\) ，可以在多项式时间内找到p，q 。

与连分数攻击相比较

\[\begin{aligned} 2-\beta-\frac{1}{2}\alpha &= 2-(\beta+\alpha) + \frac{1}{2}\alpha \\ &\le 2-\sqrt{2\beta\alpha} + \frac{1}{2}\alpha \\ &< 2-\sqrt{2\beta\alpha} - \epsilon \end{aligned} \]

所以Coppersmith 方法的界比连分数攻击的界要大很多。如果能用Coppersmith方法那么连分数方法应该也能用。

证明

对于N>5

\[(p^2-1)(q^2-1)>N^2-\frac{5}{2}N+1>\frac{1}{2}N^2 \]

那么

\[k=\frac{e d-1}{\left(p^{2}-1\right)\left(q^{2}-1\right)}<\frac{2 e d}{N^{2}}=2 N^{\alpha+\delta-2} \]

这个不等式给出了k的一个上界。同时密钥关系的式子可以写成

\[(-k)(p-q)^{2}-(N-1)^{2}(-k)+1 \equiv 0 \quad(\bmod e) \]

考虑这个多项式 \(f(x, y)=xy+Ax+1\) ，\(A=-(N-1)^2\) 。\((x, y)=(-k,(p-q)^2)\) 是 \(f(x, y)\equiv 0 \pmod{e}\) 的一个解。对这个多项式 \(F(x, u)=u+Ax, u=xy+1\) 可以用Coppersmith方法求出小根。

\[|x|<2 N^{\alpha+\delta-2}, \quad|y|<N^{2 \beta}, \quad|u|<2 N^{\alpha+\delta+2 \beta-2} \]

令 m 和 t 是正整数。考虑下面的多项式

\[\begin{array}{l} G_{k, i_{1}, i_{2}, i_{3}}(x, y, u)=x^{i_{1}} F(x, u)^{k} e^{m-k} \\ \text { with } k=0, \ldots m, i_{1}=0, \ldots, m-k, i_{2}=0, i_{3}=k, \\ H_{k, i_{1}, i_{2}, i_{3}}(x, y, u)=y^{i_{2}} F(x, u)^{k} e^{m-k} \\ \text { with } i_{1}=0, i_{2}=1, \ldots t, k=\left\lfloor\frac{m}{t}\right\rfloor i_{2}, \ldots, m, i_{3}=k . \end{array} \]

其中把 \(H_{k, i_{1}, i_{2}, i_{3}}(x, y, u)\) 进行展开，把每一项 \(xy\) 用 \(u-1\) 来替代，这样 \(G_{k, i_{1}, i_{2}, i_{3}}(x, y, u)\) 和 \(H_{k, i_{1}, i_{2}, i_{3}}(x, y, u)\) 都会变成单项式。

• 单项式 \(G_{k, i_{1}, i_{2}, i_{3}}(x, y, u)\) 依照下面这个output排列

  \(for\ k=0, \ldots m , for\ i_{1}=0, \ldots, m-k , for\ i_{2}=0 , for\ i_{3}=k , output\ x^{i_{1}} y^{i_{2}} u^{i_{3}}\)

• 单项式 \(H_{k, i_{1}, i_{2}, i_{3}}(x, y, u)\) 依照下面这个output排列

  \(for\ i_{1}=0 , for\ i_{2}=1, \ldots t , for\ k=\left\lfloor\frac{m}{t}\right\rfloor i_{2}, \ldots, m , for\ i_{3}=k , output\ x^{i_{1}} y^{i_{2}} u^{i_{3}}\)

然后我们令

\[X=2 N^{\alpha+\delta-2}, \quad Y=N^{2 \beta}, \quad U=2 N^{\alpha+\delta+2 \beta-2} \]

然后多项式 \(G_{k,i_1,i_2,i_3}(Xx,Yy,Uu)\) 和 \(H_{k,i_1,i_2,i_3}(Xx,Yy,Uu)\) 可以构成一个格 \(\mathcal{L}\) 。以 \(m=t=2\) 为例

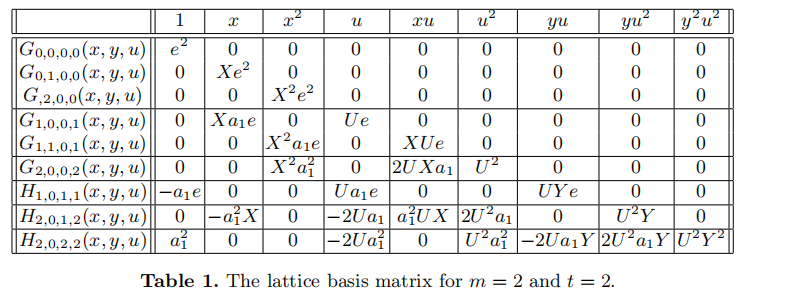
由于是下三角矩阵，这个格基的行列式为下面的形式

\[\operatorname{det}(\mathcal{L})=X^{n_{X}} Y^{n_{Y}} U^{n_{U}} e^{n_{e}} \]

其中 \(n_X,n_Y,n_U\) 和 格基的维 \(\omega\) 等于

\[\begin{aligned} n_{X} & =\sum_{k=0}^{m} \sum_{i_{1}=0}^{m-k} i_{1}=\frac{1}{6} m^{3}+o\left(m^{3}\right) \\ n_{Y} & =\sum_{i_{2}=1}^{t} \sum_{k=\left\lfloor\frac{m}{t}\right\rfloor}^{m} i_{2}=\frac{1}{2} m t^{2}-\frac{1}{3}\left\lfloor\frac{m}{t}\right\rfloor t^{3}+o\left(m t^{2}\right) \\ n_{U} & =\sum_{k=0}^{m} \sum_{i_{1}=0}^{m-k} k+\sum_{i_{2}=1}^{t} \sum_{k=\left\lfloor\frac{m}{t}\right\rfloor}^{m} k=\frac{1}{6} m^{3}+\frac{1}{2} m^{2} t-\frac{1}{6}\left\lfloor\frac{m}{t}\right\rfloor^{2} t^{3}+o\left(m^{3}\right) \\ n_{e} & =\sum_{k=0}^{m} \sum_{i_{1}=0}^{m-k}(m-k)+\sum_{i_{2}=1}^{t} \sum_{k=\left\lfloor\frac{m}{t}\right\rfloor}^{m}(m-k) \\ & =\frac{1}{3} m^{3}+\frac{1}{2} m^{2} t+\frac{1}{6}\left\lfloor\frac{m}{t}\right\rfloor^{2} t^{3}-\frac{1}{2}\left\lfloor\frac{m}{t}\right\rfloor m t^{2}+o\left(m^{3}\right) \\ \omega & =\sum_{k=0}^{m} \sum_{i_{1}=0}^{m-k} 1+\sum_{i_{2}=1}^{t} \sum_{k=\left\lfloor\frac{m}{t}\right.}^{m} 1=\frac{1}{2} m^{2}+m t-\frac{1}{2}\left\lfloor\frac{m}{t}\right\rfloor t^{2}+o\left(m^{2}\right) \end{aligned} \]

用 \(1/\tau\) 来代替 \(\left\lfloor\frac{m}{t}\right\rfloor\) ，并且使用一些近似得到

\[\begin{aligned} n_{X} & =\frac{1}{6} m^{3}+o\left(m^{3}\right) \\ n_{Y} & =\frac{1}{6} \tau^{2} m^{3}+o\left(m^{3}\right) \\ n_{U} & =\frac{1}{6}(2 \tau+1) m^{3}+o\left(m^{3}\right), \\ n_{e} & =\frac{1}{6}(\tau+2) m^{3}+o\left(m^{3}\right) \\ \omega & =\frac{1}{2}(\tau+1) m^{2}+o\left(m^{2}\right) \end{aligned} \]

对上面的格基进行LLL规约，新的格基有三个多项式 \(h_1(x,y,z)\) ， \(h_2(x,y,z)\) 和 \(h_3(x,y,z)\) 共有一个根 \((x, y, z)=(-k,(p-q)^2,-k(p-q)^2+1)\)​ ，然后用Grobner basis，可以得到 \(p-q=\sqrt{y}\) 再结合 \(N=pq\) 就可以分解N。

简单总结一下，在一开始看这一节的时候很多地方没看懂，看到对 \(F(x, u)=u+Ax\) 用 Coppersmith 方法可以解出根我以为直接用 sage 的 small_root 就可以解，然后去试了一下发现解不出来。然后硬啃下了后面的部分，感觉应该是使用了Coppersmith 的原理，自己构造单项式和多项式吧。

• Coppersmith method 攻击适用于 \(\delta < 2-\sqrt{2\alpha\beta}-\epsilon\) ，但实际上用 \(\delta < 2-\sqrt{2\alpha\beta}\) 粗略的判断一下也可以。
• 选取参数 m 和 t 构造格基，LLL规约后利用Grobner basis解出一个根(x, y, z)，其中 \(\sqrt{y}=p-q\) 再结合 \(N=pq\) 分解 N。

dome

实现起来比连分数要复杂很多，参考了一些RCTF 2022 Clearlove 的题解，东拼西凑写出来的。

from sage.all import *

beta = 0.44
n_bits = 1024
delta = 0.63
p = random_prime(1 << (n_bits//2), lbound=1<<(n_bits//2 - 1))
pqdiff_bound = 1 << int(n_bits * beta)
pqdiff_lower_bound = 1 << int(n_bits * beta - 1)
q = next_prime(p - random_prime(pqdiff_bound, lbound=pqdiff_lower_bound))
assert p > q and p < 2*q
N = p*q
phi = (p**2-1)*(q**2-1)
d_bound = 1 << int(n_bits*delta)
d_lower_bound = 1 << int(n_bits * delta - 1)
while True:
    d = random_prime(d_bound, lbound=d_lower_bound)
    if gcd(d, phi) == 1:
        e = inverse_mod(d, phi)
        if gcd(e, phi) == 1:
            break
alpha = int(e).bit_length() / n_bits
print(f"alpha={alpha}, beta={beta}, delta={delta}")
print(f"is delta < sqrt(2*alpha*beta)? {delta < sqrt(2*alpha*beta)}")
import logging
logging.basicConfig(level=logging.DEBUG)
def find_roots_univariate(x, polynomial):
    """
    Returns a generator generating all roots of a univariate polynomial in an unknown.
    :param x: the unknown
    :param polynomial: the polynomial
    :return: a generator generating dicts of (x: root) entries
    """
    if polynomial.is_constant():
        return

    for root in polynomial.roots(multiplicities=False):
        if root != 0:
            yield {x: int(root)}
def find_roots_groebner(pr, polynomials):
    """
    Returns a generator generating all roots of a polynomial in some unknowns.
    Uses Groebner bases to find the roots.
    :param pr: the polynomial ring
    :param polynomials: the reconstructed polynomials
    :return: a generator generating dicts of (x0: x0root, x1: x1root, ...) entries
    """
    # We need to change the ring to QQ because groebner_basis is much faster over a field.
    # We also need to change the term order to lexicographic to allow for elimination.
    gens = pr.gens()
    s = Sequence(polynomials, pr.change_ring(QQ, order="lex"))
    while len(s) > 0:
        G = s.groebner_basis()
        logging.debug(f"Sequence length: {len(s)}, Groebner basis length: {len(G)}")
        if len(G) == len(gens):
            logging.debug(f"Found Groebner basis with length {len(gens)}, trying to find roots...")
            roots = {}
            for polynomial in G:
                vars = polynomial.variables()
                if len(vars) == 1:
                    for root in find_roots_univariate(vars[0], polynomial.univariate_polynomial()):
                        roots |= root

            if len(roots) == pr.ngens():
                yield roots
                return
            return
        else:
            # Remove last element (the biggest vector) and try again.
            s.pop()
def factorit(N, y):
    pqdiff = ZZ(sqrt(y))
    assert pqdiff^2 == y
    x = var("x")
    roots = (x*(x + pqdiff) - N).roots()
    p = ZZ(max(r for r, _ in roots))
    assert ZZ(N) % p == 0
    q = ZZ(N) // p
    return p, q


m=8
tau = (alpha - delta - 2. * beta) / (alpha * beta)
# t = ceil(tau * m)
t=12
print(f"m={m}, t={t}")
A = -(N - 1)**2
R = PolynomialRing(QQ, 'x, y, u')
x, y, u = R.gens()
Rquo = R.quo(x*y - (u - 1))
F = u + A*x
X = ZZ(ceil(2*N**(alpha+beta-2)))
Y = ZZ(ceil(N**(2*beta)))
U = ZZ(ceil(2*N**(beta+beta+2*beta-2)))

def G(k, i1, i2, i3):
    return x**i1 * F**k * e**(m - k)

def H(k, i1, i2, i3):
    return Rquo(y**i2 * F**k * e**(m - k)).lift()
polynomials = []
monomials = []
for k in range(m + 1):
    for i1 in range(m - k + 1):
        polynomials.append(G(k, i1, 0, k))
        monomials.append(x**i1*u**k)
for i2 in range(1, t + 1):
    for k in range(m//t * i2, m + 1):
        polynomials.append(H(k, 0, i2, k))
        monomials.append(y**i2*u**k)
L = Matrix(ZZ, nrows=len(polynomials), ncols=len(monomials))
for r, g in enumerate(polynomials):
    for v, M in g(x=X*x, y=Y*y, u=U*u):
        L[r,monomials.index(M)] = v
def mprint(M):
    print("\n".join(''.join("0X"[bool(x)] for x in r) for r in M))
# mprint(L)
B = L.LLL()

polys = list(B * vector([m / m.monomials()[0](x=X, y=Y, u=U) for m in monomials]))
print(len(polys))
RR = PolynomialRing(QQ, 'xx, yy')
xx, yy = RR.gens()
def inj(f): return RR(f(u=xx*yy + 1, x=xx, y=yy))

for roots in find_roots_groebner(RR, list(map(inj, polys))):
    print(f"{A = }")
    print(roots)
    if (roots[xx] * roots[yy] + A * roots[xx] + 1) % e != 0:
        print("Not an actual root for f")
    _y = roots[yy]
    if not is_square(_y):
        print("Not a square")
        continue
    if _y > 0:
        print(factorit(N, ZZ(_y)))
        exit()

在测试这段代码的时候发现表现的并不理想，用上面这个参数跑了10分钟左右也没有跑出来。也有可能是我哪里写错了？

后来找到了HFCTF2022出题人的github上有类似的exp，看了一下，他方法也是Coppersmith，也是从

\[(-k)(p-q)^{2}-(N-1)^{2}(-k)+1 \equiv 0 \quad(\bmod e) \]

这个方程下手，构造这样的多项式

\[F=xy^2+Ax+1, \ where\ A=-(N-1)^2 \]

发现仅仅是把这篇论文中的 \((p-q)^2=y\) 替换成 \(p-q=y\) ，也就是说 \((x,y)=(-k,p-q)\) 是这个多项式的根。

以及单项式变成

\[G_{k, i_1,i_2}(x,y)=x^{i_1-k}y^{i_2-2k}F(x,y)^{k}e^{m-k} \\ H_{k, i_1,i_2}(x,y)=y^{i_2-2k}F(x,y)^{k}e^{m-k} \]

发现这个样子构造出来的格的维度要比这篇论文中的小一点点，可能就是这一点点，让这种方法的LLL格基规约速度更快吧。下面贴一下代码。

from gmpy2 import next_prime, iroot
from Crypto.Util.number import getPrime, inverse, GCD, bytes_to_long, long_to_bytes
from sage.all import *
import time

def attack2(N, e, m, t, X, Y):
    ti=time.time()
    PR = PolynomialRing(QQ, 'x,y', 2, order='lex')
    x, y = PR.gens()
    A = -(N-1)**2
    F = x * y**2 + A * x + 1

    G_polys = []
    # G_{k,i_1,i_2}(x,y) = x^{i_1-k}y_{i_2-2k}f(x,y)^{k}e^{m-k} 
    for k in range(m + 1):
        for i_1 in range(k, m+1):
            for i_2 in [2*k, 2*k + 1]:
                G_polys.append(x**(i_1-k) * y**(i_2-2*k) * F**k * e**(m-k))

    H_polys = []
    # y_shift H_{k,i_1,i_2}(x,y) = y^{i_2-2k} f(x,y)^k e^{m-k}
    for k in range(m + 1):
        for i_2 in range(2*k+2, 2*k+t+1):
            H_polys.append(y**(i_2-2*k) * F**k * e**(m-k))

    polys = G_polys + H_polys
    monomials = []
    for poly in polys:
        monomials.append(poly.lm())
    
    dims1 = len(polys)
    dims2 = len(monomials)
    MM = matrix(QQ, dims1, dims2)
    for idx, poly in enumerate(polys):
        for idx_, monomial in enumerate(monomials):
            if monomial in poly.monomials():
                MM[idx, idx_] = poly.monomial_coefficient(monomial) * monomial(X, Y)
    print(f"LLL dimension: {MM.nrows()}x{MM.ncols()}")
    B = MM.LLL()
    found_polynomials = False

    for pol1_idx in range(B.nrows()):
        for pol2_idx in range(pol1_idx + 1, B.nrows()):
            P = PolynomialRing(QQ, 'a,b', 2)
            a, b = P.gens()
            pol1 = pol2 = 0
            for idx_, monomial in enumerate(monomials):
                pol1 += monomial(a,b) * B[pol1_idx, idx_] / monomial(X, Y)
                pol2 += monomial(a,b) * B[pol2_idx, idx_] / monomial(X, Y)

            # resultant
            rr = pol1.resultant(pol2)
            # are these good polynomials?
            if rr.is_zero() or rr.monomials() == [1]:
                continue
            else:
                print(f"found them, using vectors {pol1_idx}, {pol2_idx}")
                found_polynomials = True
                break
        if found_polynomials:
            break

    if not found_polynomials:
        print("no independant vectors could be found. This should very rarely happen...")


    PRq = PolynomialRing(QQ, 'z')
    z = PRq.gen()
    rr = rr(z, z)
    soly = rr.roots()[0][0]

    ppol = pol1(z, soly)
    solx = ppol.roots()[0][0]
    return solx, soly


beta = 0.44
n_bits = 1024
delta = 0.63
p = random_prime(1 << (n_bits//2), lbound=1<<(n_bits//2 - 1))
pqdiff_bound = 1 << int(n_bits * beta)
pqdiff_lower_bound = 1 << int(n_bits * beta - 1)
q = next_prime(p - random_prime(pqdiff_bound, lbound=pqdiff_lower_bound))
assert p > q and p < 2*q
n = p*q
phi = (p**2-1)*(q**2-1)
d_bound = 1 << int(n_bits*delta)
d_lower_bound = 1 << int(n_bits * delta - 1)
while True:
    d = random_prime(d_bound, lbound=d_lower_bound)
    if gcd(d, phi) == 1:
        e = inverse_mod(d, phi)
        if gcd(e, phi) == 1:
            break
nbits = n_bits
alpha = ZZ(e).nbits() / ZZ(n).nbits()
print(f"alpha={alpha}, beta={beta}, delta={delta}")
print(f"is delta < sqrt(2*alpha*beta)? {delta < sqrt(2*alpha*beta)}")
X = 2 ** int(nbits*(alpha+delta-2)+3)
Y = 2 ** int(nbits*beta+3)
t = time.time()
x, y = map(int, attack2(n, e, 8, 12, X, Y))

p_minus_q = y
p_plus_q = iroot(p_minus_q**2 + 4 * n, 2)[0]

p = (p_minus_q + p_plus_q) // 2
q = n // p
print(f"p = {p}")
print(f"q = {q}")
print(f"if attack successfully? {p*q == n}")

跑了几次，大概5，6分钟左右就出了。