好题集锦
近期做到的一些好题，将题解收录于此，
本贴仍在施工中，由于篇幅问题，部分题目会专门写一篇博客，这里只放链接。
「HAOI2017」字符串
给定字符串 \(s\) 以及 \(n\) 个字符串 \(p_i\) 求每个 \(p_i\) 在 \(s\) 中出现的次数。但特殊的是，此处定义两个字符串 \(s,t\) 相等当且仅当 \(|s|=|t|\) 且对于任意 \(s_i\not=t_i\) 与 \(s_j\not= t_j\) 都有 \(|i-j|< k\)，其中 \(k\) 是给定常数。\(|s|,\sum |p_i|\le 2\times 10^5\)。
view solution
可以发现题目中的相等的后一个条件就相当于 \(lcp(s,t)+lcs(s,t)\ge |s|-k\)。
于是可以想到对于每个 \(p_i\) 暴力枚举 \(lcp\) 是多少，然后再在对应的 \(s\) 子串中找到满足 \(lcs\) 条件的串数量。
关于 \(lcp,lcs\) 的限制可以想到放到 \(AC\) 自动机上完成。对所有的 \(p\) 及其反串建立 \(AC\) 自动机，枚举 \(p\) 的每一个前缀 \(p[1,i]\) 作为 \(lcp\)，不妨设 \(p[1,i]\) 与 \(s[j-i+1,j]\) 匹配，那么必须有 \(p[i+k+1,|p|]\) 是后缀 \(s[j+k+1,|s|]\) 的前缀。这两个条件分别意味着：
- \(s[1,j]\) 在正串 fail 树上的节点，在 \(p[1,i]\) 的子树中。
- \(s[j+k+1,|s|]\) 在反串 fail 树上的节点，在 \(p[i+k+1,|p|]\) 的子树中。
于是可以首先预处理出 \(s,p\) 的每个前缀/后缀对应的节点，并将 \(s[j+k+1,|s|]\) 对应的节点标记在 \(s[1,j]\) 上。那么暴力做可以直接找到 \(p[1,i]\) 的节点后，暴力对于子树内的所有 \(s[1,j]\) ，将其上标记的点全部点亮，然后查询 \(p[i+k+1,|p|]\) 子树内有多少个被点亮的点即可。使用 \(dfs\) 来实现，经过每一个点都将其上标记的点点亮，并在进入点 \(u\) 以及离开点 \(u\) 时分别统计一遍答案，即可实现子树查询。
你会发现这样做会算重，因为当 \(lcp+lcs> s-k\) 时会在 \([s-k-lcs,lcp]\) 之间都被计算一次，考虑强制要求它只在 \(s-k-lcs\) 被算到，也就是说还有满足 \(p[i+k+1,|p|\) 不是 \(s[j+k,|s|]\) 的前缀，这个问题可以用同样的方法计算后减掉即可。
「JOISC 2020 Day2」遗迹
有一个长度为 \(2n\) 的高度序列 \(h\)，其中 \(1\sim n\) 每个数都恰好出现了 \(2\) 次。
之后进行了若干次操作，每次操作会让满足存在 \(i<j,h_i=h_j\) 的 \(i\) 的 \(h\) 减一。如果 \(h\) 为 \(0\) 则不再下降。
当进行了 \(n\) 次操作后，一定只剩下 \(n\) 个 \(h\) \(\not=0\)，现在给出这 \(n\) 个 \(h\) 的位置，问最初 \(2n\) 个石柱的高度的方案数。
\(n\le 600\)。
view solution
考虑初始的 $h$ 确定后，求出每个石柱最后的高度：从右往左考虑每个石柱 $i$，它的最终高度应当是最大的满足 $1\le j\le h_i$ 且没有被占领的 $j$，然后 $j$ 占领。如果不存在这样的 $j$，最终高度即为 $0$。可以发现最终高度是否为 \(0\) 取决与自己的高度，以及最大的 \(j\) 满足 \(\forall i\in[1,j]\)，高度 \(i\) 都已被占领，我们称这样的 \(j\) 为不合法前缀长度 \(len\)。
于是可以想到从右至左 \(dp\)，记录 \(f_{i,j}\) 表示已经选定了 \([i,2n]\) 的高度，\(len\) 为 \(j\) 时的方案数。为了方便，我们将高度相同的两根柱子看作不同的高度，最后答案再除以 \(2^n\)。
设 \(s0,s1\) 分别表示 \([i+1,2n]\) 柱子中有多少个柱子没有保留下来/保留了下来。转移分几种情况：
-
\(i\) 号柱子没有保留下来：那么必然有 \(h_i\in[1,j]\)，在可选的 \(2j\) 个高度中，\(j\) 个分别占领 \(1\sim j\)，\(s0\) 个分配给了之前没保留下来的柱子，因此可选方案为 \(j-s0\)。\(f_{i,j}\gets f_{i+1,j}(j-s0)\)。
-
\(i\) 号柱子被保留下来，不妨设最终 \(i\) 号柱子的高度变为了 \(w\)。
-
\(w>j+1\)：那么它不会改变不 \(len\)，可以使用经典的延迟转移套路，先不选择它的高度，等之后极长不合法前缀长度 \(\ge w\) 之后，再来选择。\(f_{i,j}\gets f_{i+1,j}\)。
-
\(w=j+1\)：再枚举现在将 \(len\) 提高到了 \(k\)，那么有 \(h_i\in[j+1,k]\)，且在 \(i\) 之前的柱子中有 \(k-j-1\) 个最终高度分别为 \(j+2,j+3,\dots k\)，选出这 \(k-j-1\) 个柱子，它们在经过一系列操作后（此时其他柱子不会影响它们）变成了长为 \(k-j-1\) 的连续段，此时它们初始高度的选择方案数记为 \(g_{k-j-1}\)，\(g\) 的转移我们稍后再说。还有选择 \(i\) 的初始高度，在 \([j+1,k]\) 范围的高度有 \(2(k-j)\) 个，去掉已经被占领的 \(k-j-1\) 个，还剩 \(k-j+1\) 个。
于是 \(f_{i,k}\gets f_{i+1,j}\binom{c_1-j}{k-j-1}g_{k-j-1}(k-j+1)\)。
-
现在考虑 \(g\) 的转移：枚举编号最小的柱子的最终高度 \(j\)，那么之后的柱子中 \(<j\) 以及 \(>j\) 的部分完全独立，可以分别递归。同样的得到它的初始高度选择方案为 \(i-j+2\)，于是有：
最终复杂度 \(\mathcal O(n^3)\)。
「NOI2018」情报中心
给定一棵 \(n\) 个点带边权的树，并给定 \(m\) 条路径，每条路径有对应的代价。要求选择两条路径使得它们至少有一条公共边，且经过边集的并的权值和减去代价和最大。
\(n\le 5\times 10^4,m\le 10^5\)。
view solution
对于合法的两条路径 \((u_i,v_i,w_i),(u_j,v_j,w_j)\)，考虑求选择它们的收益，直接将 \(w_i\) 与 \(w_j\) 加起来会将两条路径共同经过的部分算两遍，直接表示公共部分很难表示。这里有一个很妙的思路：改为考虑把没有共同经过的部分也算两遍，可以发现没有共同经过的部分就是 \(path(u_i,u_j)\) 与 \(path(v_i,v_j)\)。于是选择这两条路径的收益的两倍就是：
记 \(c_i=dis(u_i,v_i)-2w_i\)，那么上面的贡献就是 \(dis(u_i,u_j)+dis(v_i,v_j)+c_i+c_j\)。
计算 \(dis\) 当然考虑 \(LCA\)，考虑枚举 \(LCA(u_i,u_j)=a\)，此时可以将上面的 \(dis(u_i,u_j)\) 代换为 \(dep_{u_i}+dep_{u_j}-2dep_a\)，于是贡献转化为：
于是可以想到将 \(v_i\) 的权值赋为 \(dep_{u_i}+c_i\) ，那么这个问题就变成了最大化 \(w_u+w_v+dis(u,v)\)。这是一个经典的带权直径问题，记 \(f(S)\) 为点集 \(S\) 的直径的端点，那么有：
于是可以用每个点 \(a\) 用线段树维护 \(a\) 子树内所有候选路径端点的集合的带权直径，每次合并子树 \(u,v\) 时计算 \(u,v\) 候选集合之间的贡献。路径 \((u,v)\) 在点 \(a\) 的候选集合内当且仅当 \(a\) 在 \(u,v\) 路径上，为了满足至少有一条边有交：\(a\) 不能为 \(LCA(u,v)\)，于是可以在 \(u,v\) 点上加入这条路径，在 \(u\rightarrow lca\) 路径上距离 \(lca\) 最近的点以及 \(v\rightarrow lca\) 路径上距离 \(lca\) 最近的点删去，删去只需要将该点的权值赋为 \(-inf\) 即可。
最终复杂度 \(\mathcal O((n+m)\log a)\)。
CF1148H Holy Diver
给定一个初始为空的数组。每次在末尾插入一个数并询问区间 \([l,r]\) 有多少子区间满足 \(mex=k\)，强制在线。
\(n\le 2\times 10^5\)。
view solution
先不考虑强制在线，离线下来倒着做维护 \(mex\)。
将右端点从右向左移动，维护每个左端点对应的答案。假设现在删除了 \(a_r=x\)，可以找到 \(x\) 的上一次出现的位置 \(las\)，将 \([las,r-1]\) 对应的 \(mex\) 修改为 \(x\)。使用珂朵莉树维护，基于染色均摊，染色的次数是 \(\mathcal O(n)\) 的。
为了强制在线，现在改为正着扫描，那么此时 \(mex\) 的修改次数也应当是 \(\mathcal O(n)\) 的。还是从左到右移动右端点，维护每个左端点对应的答案。假设现在加入了 \(a_i=x\)，找到当前 \(mex=x\) 的区间 \([l,r]\)，再找到最小的 \(y\) 满足 \(y\) 的最后一次出现位置 \(<r\)，则 \([las_y+1,r]\) 的 \(mex\) 应该被修改为 \(y\)，其中 \(las_y\) 为 \(y\) 的最后一次出现位置，然后在将原本 \(mex=y\) 的区间与 \([l,las_y]\) 拼起来继续递归处理即可。每次递归都会改变一段区间的 \(mex\)，因此递归次数应当是 \(\mathcal O(n)\) 的。
考虑如何回答询问，将 \(l,r\) 看作平面上的两维，那么 \(mex=k\) 的区间的出现位置就是一个矩形，询问就是询问一个矩形与这些矩形的交，也就是矩形加矩形求和，可以使用可持久化线段树维护历史版本和实现，注意到所有矩形都是不交的，可以只在矩形的左右边界出修改线段树中维护的历史版本和，可以进行标记永久化，大大减小常数。
CF1416E Split
给定长为 \(n\) 的序列 \(a\)，求长度为 \(2n\) 的序列 \(b\) 满足：
- \(\forall i\in[1,n],b_{2i-1}+b_{2i}=a_i\)。
- 将 \(b\) 的值相同的连续段缩成一个数后，\(b\) 的长度最小。
求这一最小长度。\(n\le 10^5\)。
view solution
可以想到朴素 \(dp\)，记 \(f_{i,j}\) 表示考虑了 \(b\) 的前 \(2i\) 个数，\(b_{2i}=j\) 时相比 \(2i\) 能减少的最大长度，有转移：
那么可以发现对于 \(\forall j\in[1,a_i-1]\)，\(f_{i,j}\) 的极差不超过 \(2\)，并且如果差值为 \(2\)，那么最大值一定只有一个数，即 \(a_i/2\)。于是可以记录当前的最小值 \(mn\)，\(=mn+2\) 的位置 \(two\)，并用 \(set\) 维护 \(dp\) 值 \(=mn+1\) 的集合 \(one\)（，这一定是一段区间加上 \(\mathcal O(1)\) 个点。
转移时，先用当前的 \(mx\) 更新所有值，作为新的 \(mn\) 分极差为 \(0,1,2\) 分别讨论：
- 极差为 \(0\)：对于 \(\forall j\in[1,a_{i-1}-1]\)，\(a_i-j\) 都会在 \(one\) 集合中，可以将 \(j\to a_i-j\) 的操作称为翻转。将区间设为 \([1,a_{i-1}-1]\) ，维护标记 \(k,b\) 表示对于 \(one\) 中的位置 \(x\)，\(kx+b\) 是实际的位置， 翻转就只需要在 \(k,b\) 上打标记就行了。
- 极差为 \(1\)：新的 \(one\) 集合时原本 \(one\) 集合翻转后的集合，特判一下 \(a_i/2\) 的位置即可。
- 极差为 \(2\)：原本的 \(two\) 会变成新的 \(one\) 集合，再特判一下 \(a_i/2\) 的位置。
最终复杂度 \(\mathcal O(n\log n)\)。
CF1456E XOR-ranges
有 \(n\) 个不超过 \(k\) 位的二进制数 \(x_i\)，第 \(i\) 个的取值范围是 \([l_i,r_i]\)，给出数列 \(c_0,c_1,\dots,c_{k-1}\)，定义 \(f(x)=sum_{i=0}^{k-1}[x\&2^i]c_i\)，要求确定 \(x_i\) 以最小化 \(\sum_{i=2}^{n}f(x_{i-1}\oplus x_i)\)。
\(n,k\le 50\)。
view solution
对于有上下界的二进制问题，一个经典套路是枚举在哪一位开始可以解出限制。具体的，\(l_i,r_i\) 在二进制位上从高到低会有一段前缀完全相同，这一部分 \(x\) 的选择是确定的，不可能解出限制；对于 \(l_i,r_i\) 第一个不同的位置，根据 \(x\) 选择 \(0/1\) 可以解出上界/下界的限制；对于接下来的数位可以在某个 \(l_i\) 当前位为 \(0\) 的位置令 \(x_i=1\) 以解除 \(l\) 的限制；或者在某个 \(r_i\) 当前位为 \(1\) 的位置令 \(x_i=0\) 以解出 \(y\) 的限制。
如果 \(x_i\) 没有了上下界限制，不妨设其左右的取值分别为 \(a,b\)，那么可以令 \(x_i=a\) 或者 \(b\)，使得贡献直接变为 \(a\oplus b\)，这显然是最优的选择。
于是可以据此进行 \(dp\)，设 \(f_{c,l,r,sx,sy}\) 表示现在考虑第 \(c\sim k-1\) 位的取值，并且 \([l,r]\) 中的数解除限制的位置 \(\ge c\)，而 \(l-1,r+1\) 解除限制的位置 \(\le c\)，\(sx,sy\) 则分别表示 \(x_{l-1},x_{r+1}\) 的 \(c\sim k+1\) 位（可以用 \(c+1\sim k-1\) 位与 \(l\) 相同还是与 \(r\) 相同，以及第 \(c\) 位是否解除了限制两个 \(bool\) 变量表示）。
转移有两种情况：
- \([l,r]\) 中的数解除限制的位置 \(> c\)，那么直接从 \(f_{c+1,l,r,sx,sy}\) 转移过来，并且将 \(x_{l-1}\oplus x_{r+1}\) 的第 \(c\) 位加入答案。
- \([l,r]\) 中有数解除限制的位置 \(=c\)，可以枚举最靠左的在第 \(c\) 为解除限制的数 \(i\)，讨论 \(i\) 是解除了 \(l\) 的限制还是 \(r\) 的限制进行转移。注意需要保证 \(l_i,r_i\) 在第 \(c+1\) 位前已经不同。
注意要特判可以一直不解除限制，直接令 \(x_i=l_i/r_i\) 的情况。
最终状态为 \(c=k\) 时必须有 \(l>r\)，否则设为 \(inf\)。
最终复杂度 \(\mathcal O(n^3k)\)，可以使用记忆化搜索实现。
CF453E Little Pony and Lord Tirek
有 \(n\) 个数，第 \(i\) 个数初始为 \(s_i\)，每经过一单位时间会增加 \(k_i\)，上限为 \(w_i\)。有 \(q\) 次操作，每次操作给出 \(t,l,r\) 询问 \(t\) 时刻编号在 \(l\sim r\) 范围内的数的和，并将它们全部变成 \(0\)。保证 \(t\) 单调递增。
\(n,q,s_i,k_i,w_i\le 10^5\)。
view solution
首先可以特判每个数第一次被访问时的情况，假设所有数初始均为 \(0\)。
考虑所有询问满足 \(l=1,r=n\) 时的情况。此时假设当前询问与上次询问的时间的差为 \(t\)，那么所有满足 \(s_i/k_i\geq t\) 的编号为 \(i\) 的数这段时间内一直增加，贡献就是 \(k_it\)；其余的数的贡献就是 \(m_i\)。
因此可以预先将所有数按照 \(s_i/k_i\) 排序，那么只需要查询 \(\le t\) 的数的 \(k_i\) 之和与 \(>t\) 的数的 \(m_i\) 之和就行了。
回到原问题，考虑将上一次被修改时间相同的一段区间拿出来一起做，这是一个二维数点问题，不难用可持久线段树做到单次 \(\mathcal O(\log n)\)。将上次被修改时间看作颜色，这是一个颜色覆盖问题，使用珂朵莉树维护，询问次数就是 \(\mathcal O(n)\) 得了。
最终复杂度 \(\mathcal O(n\log n)\)。
CF1188D Make Equal
给出 \(n\) 个数字 \(a_i\) ，每次操作可以给其中一个数加上 \(2\) 的非负整数次幂。
求最少的操作次数，使得这 \(n\) 个数相等，\(n\le 10^5\) 。
view solution
第 \(i\) 位进位的数一定是按前 \(i\) 位的值从大到小排序后的一个后缀。
容易想到数位 \(dp\) 最终的 \(a_i\)，但减法不是我们喜欢的，先将所有 \(a\) 加到 \(\max a_i\)，再枚举接下来加的数 \(x\)。令 \(a_i=\max a_i-a_i\)，那么所求即为：
考虑数位 \(dp\)，定义 \(dp_{i,j}\) 表示考虑了最低的 \(i\) 个二进制位，当前位有 \(j\) 个数进位了。注意到进位的数一定是将所有数最低 \(i\) 个二进制位的值从大到小排序后的一段前缀，因此我们只需要记录数量即可表示整个状态！
转移就只需要讨论一下当前位填 \(0/1\) 了，最终复杂度为 \(\mathcal O(n\log a_i\log n)\)，当然可以基数排序优化到 \(\mathcal O(n\log a)\)。
CF1656H Equal LCM Subsets
给定两个正整数集合 \(A,B\)，要求构造非空集合 \(S_A\subset A,S_B\subset B\)，使得 \(S_A\) 中元素的 \(lcm\) 与 \(S_B\) 中元素的 \(lcm\) 相同。
\(n,m\le 1000,a_i,b_i\le 4\times 10^{36}\)。
view solution
首先考虑如何判断两个集合是否合法。一个容易想到的思路是对每个质因子分别判断，但值域过大以至于无法质因数分解。考虑对 \(A,B\) 中的每个元素分别考虑，对 \(A\) 中的每个元素 \(a\) 定义 \(f(a)=\gcd(a/\gcd(a,b_1),a/\gcd(a,b_2),\dots,a/\gcd(a,b_m))\)，类似的定义 \(g(b)\)。可以发现如果 \(f(a)>0\) 就表示 \(a\) 中的某些因数 \(b\) 中不含有，则 \(A\) 的 \(lcm\) 一定不等于 \(B\) 的 \(lcm\)，因此合法的充要条件就是所有的 \(f(a),g(b)\) 都等于 \(1\)。
考虑从初始集合出发不断删除得到最终答案，注意到如果 \(f(a)>1\)，那么 \(a\) 只要存在则 \(A\) 的 \(lcm\) 一定含有 \(B\) 的 \(lcm\) 中不含有的因子，因此 \(a\) 必须要被删掉，类似的进行 \(b\) 的删除 。不断进行删除，在删除时用线段树维护 \(f(a),g(b)\) 的变化情况，直到最终 \(f(a)=g(b)\) 都等于 \(1\) 为止。最终的复杂度为 \(\mathcal O(n^2\log nU)\)，其中 \(U=\log 10^{36}\) 为 \(\gcd\) 的复杂度。
CF1656G Cycle Palindrome
给定一个长为 \(n\) 的序列 \(\{a_i\}\)，要求你给出一个排列 \(p_i\)，使得新序列 \(a_{p_1},a_{p_2},a_{p_3},\dots,a_{p_n}\) 是回文序列且排列 \(p_i\) 在将 \(i\) 向 \(p_i\) 连边后生成的图只有一个环。
\(n\le 2\times 10^5\)。
view solution
不难发现原问题有解的必要条件是至多只有一种数字出现了奇数次，且出现了奇数次的那个数字不能只在 \(\frac{n+1}{2}\) 处出现（否则一定会形成一个自环）。可以构造证明这也是充分条件。
对于这种有许多限制的构造问题，首先假设不存在排列只有一个环的限制，先生成一个使得 \(a_{p_1},a_{p_2},\dots,a_{p_n}\) 为回文序列的排列，这是容易实现的。建出此时的图，考虑通过交换两个不在同一个环上的编号的 \(p\) 来合并这两个环。首先 \(p_i\) 与 \(p_{n+1-i}\) 显然是可以随意交换的，可以先直接交换使得 \(i\) 与 \(n+1-i\) 在一个环中。
对于此时原图中的环，可以想到是否能够整体交换 \(p_i\) 与 \(p_j\)，\(p_{n+1-i}\) 与 \(p_{n+1-j}\) ，如果 \(i\) 与 \(n+1-i\) 两个点构成了一个环，这样做就没用了。但这个想法可以延伸，考虑从每个环中各取出一个位置 \(c_1,c_2,\dots,c_k\)，将 \(p_{c_1}\) 改为 \(p_{n+1-c_2}\)，\(p_{c_2}\) 改为 \(p_{n+1-c_3}\)，\(\dots\)，\(p_{c_{k-1}}\) 改为 \(p_{n+1-c_k}\)，\(p_{c_k}\) 改为 \(p_{c_1}\)。为了保持回文，同时将 \(p_{n+1-c_1}\) 改为 \(p_{c_2}\)，\(p_{n+1-c_2}\) 改为 \(p_{c_3}\) \(\dots\)，\(p_{n+1-c_{k-1}}\) 改为 \(p_{c_k}\)，\(p_{n+1-c_k}\) 改为 \(p_{n+1-c_1}\)。这样就成功的合并为了一个环，结合下图观看更佳。
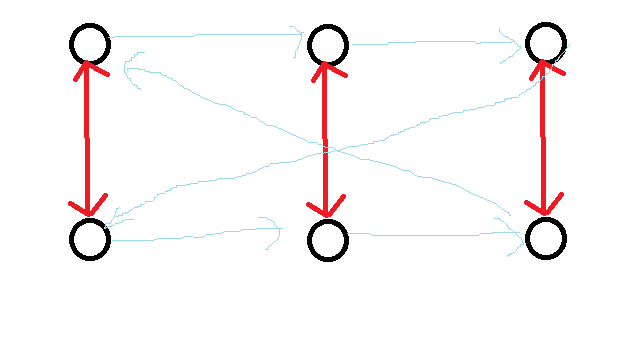
注意到这一构造需要满足 \(c_i\not= n+1-c_i\) ，因此如果选择 \(c\) 时要避开 \(\frac{n+1}{2}\)，在满足了上面的必要条件后这是一定可以做到的。
CF1067D Computer Game
有 \(n\) 个游戏，每个游戏有收益 \(a_i\)， 升级后的收益 \(b_i\)，玩游戏有 \(p_i\) 的概率成功。每秒可以玩一个游戏，如果成功则得到当前收益，并且可以升级任意某个游戏。求 \(t\) 秒后的期望收益的最大值。\(n\le 10^5,t\le 10^{10},a_i\le b_i\)。
view solution
不难发现只要成功了一次，一定会选择升级 \(b_ip_i\) 最大的游戏并一直玩这个游戏。
成功之前的部分可能需要进行 \(DP\)，记 \(f_i\) 表示还剩 \(i\) 秒时间并且还未成功过，接下来 \(i\) 秒能获得的最大收益的期望，记 \(mx=\max_{i=1}^{n}b_ip_i\)。
有转移：
记 \(S_i=i\times mx-f_i\)，可以进一步处理为
这是一个斜率优化的形式，将每个游戏看作点 \((p_j,p_ja_j)\) ，那么最优转移点就是用斜率为 \(-S_{i-1}\) 的直线去切得到的结果。由于 \(f_{i+1}-f_i\) 显然不会超过 \(mx\)，因此斜率 \(-S_{i-1}\) 单调不降，可以做到 \(\mathcal O(t)\)。
一段的转移都是同一个转移点时，转移形如 \(f_j=p_ja_j+p_jS_{i-1}+f_{i-1}\)，可以写作矩阵的形式用，矩阵快速幂优化。
预处理当前矩阵的 \(2^k\)，倍增找出转移点变化的位置即可，复杂度是 \(\mathcal O(3^3n\log t)\)。
[九省联考 2018] IIIDX
给定 \(n,k\) 及权值序列 \(d\)，要求重新排列 \(d\) 使得 \(\forall i\in[1,n],d_i\ge d_{i/k}\) 并且 \(d\) 的字典序最大。
\(n\le 500000,d_i\le 10^9\)。
view solution
将 \(i\) 向 \(i/k\) 连边，得到一棵树，要求树上每个点的权值都小于等于其子树中所有点的权值。将 \(d\) 从大到小排序，那么不难发现每个点子树中所有点的权值一定是一个连续的区间。
按编号从小到大考虑点 \(i\)，贪心地选择最大的 \(d_i\) 使得 \(d_{i+1}\sim d_n\) 可以通过合理重排使得满足条件，这可以通过对 \(\forall i\) 维护 \(f_i\) 表示 \(\ge i\) 数中还有多少个可供选择。那么在处理到点 \(i\) 时，\(d_i\) 就应当是最大的 \(j\) 满足 \(f_j\ge siz_i\) 。如果有多个 \(d_i\) 都等于 \(j\)，选择最右的一个一定最优。
现在考虑确定了一个新点 \(i\) 对 \(f\) 带来的影响。此时 \(\ge d_i\) 的数中有 \(siz_i\) 个被选择了， 新增节点 \(i\) 的限制，对 \(j\in [1,d_i]\) ，\(f_j-=siz_i\)，但对于子树 \(i\) 中用到的 \(>d_i\) 的权值，它们的 \(f\) 变化并不相同，难以处理，但注意到这些权值都已经被用完了，在子树 \(i\) 外还未确定的子树中一定不会被用到，我们只需要保证当查询的值 \(v\) 满足 \(f_{d_j}\ge v\) 时会直接走到 \(d_j\) 而不会到这些权值即可。这可以将限制改为 \(\forall k\le j,f_k\ge v\)，然后用线段树维护区间 \(\min\) 后二分即可。注意考虑点 \(u\) 时，应当将其父亲之前的限制给去掉。
CF1188E Problem from Red Panda
有 \(k\) 个非负整数 \(a_1\sim a_k\)，每一次操作可以将选择一个数 \(i\in [1,k]\)，将 \(a_i+=k\)，再让所有数 \(-1\)，但不能让任何一个数变成负数。你可以进行任意次操作，问最终能得到多少种不同的 \(a\) 序列。
\(k\le 10^5,\sum_{i=1}^{k}a_i\le 10^6\)。
view solution
考虑如何处理 \(a_i\) 不能变成负数的限制。可以发现这相当于在前 \(a_i+1\) 次操作中至少有一个选择了 \(i\)，前 \(a_i+k+1\) 次操作中至少有两个选择了 \(i\) \(\dots\)。在这些位置打上标记作前缀和，便可得到 \(s_i\) 表示前 \(i\) 次操作中有多少个已经被钦定了作用对象。那么如果 \(s_i> i\) 则操作的轮数必须 \(<i\)。因此我们可以得到一个操作轮数的上限 \(lim\)。
可以发现 \(lim\) 如果不是无穷大，就一定 \(\le k\)，因为如果前 \(k\) 次操作合法，后面的第 \(i\) 次操作只需要复刻第 \(i-k\) 次操作就行了。
如果 \(lim<k\) ，此时存在关键性质：对于任意两个操作方案，如果它们对某一个数的操作次数不相同，则最终得到的序列也不相同（否则对该数的操作次数差必须 \(\ge k\)，显然不合法）。于是我们只需要统计序列 \(\{c_i\}\) 的数量，其中 \(c_i\) 表示对第 \(i\) 个数的操作数。这可以通过隔板法 \(\mathcal O(1)\) 求出。
如果 \(lim\) 是无穷大，此时如果序列 \(\{b_i\}\) 可以被 \(p\) 次操作得到，那么一定能被 \(p+k\) 次操作得到，但反过来不一定。但是当 \(p>\max(a_i)\) 步数足够多，反过来也成立。同时如果两个操作序列的操作次数 \(\pmod k\) 不同余则一定不会得到相同的结果，所以只用考虑 \([10^6,10^6+k]\) 区间内的操作次数，复杂度为 \(\mathcal O(\max a_i+k)\).
CF1610I Mashtali vs AtCoder/AGC017D Game on Tree
A 与 B 在一个 \(n\) 个点的树上玩游戏。树上有若干个关键点，A,B 轮流操作，A先手。每轮操作的人可以删去树上的任何一条边，生成的两个连通块中，如果某个连通块不存在任何一个关键点则将其删去。无法操作的人失败。
现在对于 \(k=1\dots n\) ，询问 \(1\sim k\) 号点为关键点时谁会获胜。\(n\le 3\times 10^5\)。
view solution
对于 \(k=1\) 的情况，将 \(1\) 作为根，那么此时每删一条边就相当于删去一个子树。
考虑 \(sg\) 函数，设 \(sg(u)\) 表示以 \(u\) 为根的子树的 \(sg\) 函数值。
在对 \(u\) 操作中，可以发现对 \(u\) 的每个儿子的子树中的操作是互不干扰的，因此可以看作将 \(u\) 的子树 \(T_u\) 分配成了 \(T_{v_1}',T_{v_2}'\dots\)，其中 \(v_i\) 是 \(u\) 的所有儿子，而 \(T_v'\) 是由 \(T_v\) 的根节点增加一条到父亲的边得到的。
对于 \(T\) 的 \(sg\) 值，这里给出结论 \(sg(T')=sg(T)+1\)。
证明考虑数学归纳法。当 \(T\) 只含有一个点是显然成立，否则 \(sg(T_u')=mex(\{sg(T_v')\},0)=mex(\{sg(T_v)+1\},0)=sg(T_u)+1\)。
因此可以树形 DP 求出 \(sg(1)\)。
对于 \(k>1\) 的情况，以 \(1\) 为根建树，将原树分为若干子问题：
- 每个极大的不含关键点的子树加上其根的父亲。它的 \(sg\) 值可以预处理出来。
- 去掉这些子树后剩余的部分，可以发现这棵树的所有叶子都是关键点，因此删去任意一条边都不会让任何一个连通块被删除。那么不难得到这棵树的 \(sg\) 值就是边数 \(\mod 2\)。
当我们需要从 \(k\) 的答案得到 \(k+1\) 的答案时，相当于将 \(k+1\) 到 \(1\) 的路径全被加入第二部分的树中，可以通过从 \(k+1\) 出发暴力往上跳，跳到关键点为止来完成。总复杂度依然是 \(\mathcal O(n)\)。
CF1609G A Stroll Around the Matrix
有一个长为 \(n\) 的序列 \(\{a_i\}\)，与一个长为 \(m\) 的序列 \(\{b_i\}\)。这两个序列都满足单增并且差分序列也单增。
现在要进行 \(q\) 次操作：
1 k d：让序列 \(a\) 的最后 \(k\) 个数分别增加 \(d,2d,3d,\dots,kd\)，也就是将序列 \(a\) 变成 \(a_1,a_2,\dots,a_{n-k},a_{n-k+1}+d,a_{n-k+2}+2d,\dots,a_n+kd\)。2 k d：对序列 \(b\) 进行同样的操作。
每次操作完后可以写出一个 \(n\times m\) 的矩阵，其中第 \(i\) 行第 \(j\) 列的权值为 \(a_i+b_j\)。请你求出从 \((1,1)\) 走到 \((n,m)\) ，只能向下或向右走，途中经过的所有位置的权值和的最小值。
\(n\le 100,m\le 10^5,q\le 10^5\)。
view solution
设 \(da_i,db_i\) 分别为 \(a,b\) 数组的差分，即 \(da_i=a_{i+1}-a_i,db_i=b_{i+1}-b_i\)。
可以发现将路径上经过的每个数差分得到的结果就是 \(da_1,da_2,\dots,da_{n-1},db_1,db_2,\dots,db_{m-1}\) 重新排列后的结果，因此如果当前在位置 \((i,j)\)，贪心地根据 \(da_i\) 与 \(db_j\) 的相对大小选择向下/向右走是正确的策略。
考虑调整法，一开始假设策略就是从 \((1,1)\) 先一直向下走到 \((n,1)\)，再一直向右走到 \((n,m)\)。接下来暴力枚举每一行贪心地考虑是否要在第 \(i\) 行先向右走，再往下走，可以发现如果在 \((i,j)\) 从向下走改为向右走，等于是将 \(db_j\) 从 \(da_{n-1}\) 后移动到 \(da_{i}\) 前，会导致答案减少：
于是我们会选择最大的满足 \(\sum_{k\ge i}da_k-(n-i)db_j>0\) 的 \(j\) ，从当前位置先向右走到 \((i,j+1)\) ，再往下走。这个 \(j\) 可以通过二分得到。
那么对于每组询问，可以 \(\mathcal O(n)\) 暴力枚举 \(i\) 以及求 \(da\) 的后缀和，用线段树维护 \(db\) 即可实现区间加以及二分 \(j\) ，最终总复杂度为 \(\mathcal O(nq\log m)\)。
洛谷P3642 [APIO2016]烟火表演
给定一棵有根树，边有边权，将某条边的边权改变 \(1\) 需要花费 \(1\) 的代价，但边权必须为非负整数。请求出使所有叶子到根路径上的边权和相同需要花费的最小代价。\(n\le 3\times 10^5\)。
view solution
经典题，在发现树形 DP 的式子是个凸函数后，可以用可并堆维护其斜率变化点（斜率范围小的时候）或者使用平衡树维护。
根据题意容易得到 \(dp\) 式子，设 \(f_{u,i}\) 表示 \(u\) 子树中所有叶子到 \(u\) 路径上的边权和均为 \(i\) 时的最小代价，那么有转移：
那么可以发现 \(f\) 是一个下凸的函数，并且每次只会将一条斜率为 \(-1/1\) 的直线叠加上去，因此斜率的范围比较小的，可以考虑用可并堆进行维护，在可并堆中维护所有的 \(x\) 满足从 \(x\) 左侧的直线到右侧的直线，斜率增加了 \(1\)。如果有多个相同的 \(x\) 就表示这个地方增加了 \(>1\) 的斜率。
在维护拐点的基础上如果还能直到起始点的纵坐标与斜率，就可以直接推出答案。而本题中起始点，也就是 \(f_{u,0}\) 就等于 \(u\) 子树中所有边的边权和，是易于求出的。
考虑转移如何维护，取出 \(f_v\) 函数中的斜率为 \(0\) 的区间 \([L,R]\)，可以将转移分为 \(4\) 段：
- \(x\le L\)，此时 \(f_u(x)\) 直接从 \(f_v(x)\) 转移一定最优，因为如果从 \(<x\) 的 \(y\) 处转移，代价 \(y+w-x\) 会增加，\(f_v\) 也会增加，一定不优。于是有 \(f_u(x)+=f_v(x)+w\)。
- \(L<x\le L+w\)，此时 \(f_u(x)\) 从 \(f_v(L)\) 转移一定最优。因为如果从 \(>L\) 的 \(y\) 转移，代价与 \(f\) 都会增大；从 \(<L\) 的 \(y\) 转移，代价每减少 \(1\)，\(f\) 至多增加 \(1\)，一定不优。于是有 \(f_u(x)+=f_v(L)+L+w-x\)。
- \(L+w<x\le R+w\)，此时直接从 \(f_v(x-w)\) 转移，代价为 \(0\) 且 \(f\) 最小：\(f_u(x)+=f_v(x-w)\)。
- \(x>R+w\)，此时总 \(f_v(R)\) 转移一定最优：\(f_u(x)+=f_v(R)+x-R-w\)。
于是相当于先将函数 \(f_v\) 的 \(\le L\) 部分向上平移，\([L,R]\) 向右平移 \(w\) 并在 \([L,L+w]\) 处增加一条斜率为 \(-1\) 的直线，将 \(R+w\) 右侧的部分替换为一条斜率为 \(1\) 的直线，再与 \(f_u\) 合并。
那么这个过程只需要先将 \(R\) 右侧的拐点全部 \(pop\) 掉，再在 \(L+w,R+w\) 处分别增加两个拐点即可。如何找到 \(L,R\) 呢，注意到 \(u\) 的所有儿子合并完后，\(u\) 的函数中的最大斜率就是其儿子个数，于是只要 \(pop\) 掉儿子个数 \(-1\) 个拐点，下一个就是 \(R\)。
使用可并堆维护，复杂度为 \(\mathcal O(n\log n)\)。
loj#2540. 「PKUWC2018」随机算法
给定一个 \(n\) 个点 \(m\) 条边的无向图，考虑通过以下算法求解最大独立集：
- 随机生成一个排列 \(p\)。
- 按照 \(p\) 的顺序依次尝试将每个点加入最大独立集中。
问以这一算法得到正确答案的概率是多少，\(n\le 20\)。
view solution
考虑对于一个独立集 \(s\)，求这个独立集被该算法在某一步中得到的概率 \(p_s\)。
枚举 \(s\) 中最后一个被加入的数 \(i\)，设加入 \(i\) 之前的集合为 \(t\)，\(f(t)\) 为所有与 \(t\) 中点不直接相连的点的集合，那么加入 \(t\) 之后下一个加入的是 \(i\) 当且仅当 \(i\) 是 \(f(t)\) 中第一个出现的，于是有：
于是可以 \(\mathcal O(n2^n)\) 求出 \(p\)，答案就是原图所有最大独立集的 \(p\) 之和。
loj#2461. 「2018 集训队互测 Day 1」完美的队列
有 \(n\) 个队列，如果第 \(i\) 个队列的 \(size>a_i\) 就会自动执行 \(pop\) 操作。现在有 \(m\) 次操作，枚举对区间 \([l,r]\) 中的所有队列同时 \(push(x)\)，询问每次操作后所有队列里有多少不同的权值。
\(n,m,a_i,x\le 10^5\)。
view solution
核心转化：转化为求出每个操作加入的所有数什么时候全部被 pop 掉，然后就可以分摊到整块与散块上分别计算 pop 的时间再取 \(\max\)。
对于整块的贡献，可以是用双指针 \(l,r\) 表示只考虑 \([1,r]\) 操作时， \([l,r]\) 操作中 push 的数还没有被 pop 掉。双指针移动的过程中可以暴力维护每个队列中 \(l\) 操作加入的数还有多久会被 pop 掉，整块操作可以直接打 tag，散块操作暴力修改。
对于散块的贡献，枚举每个块内的所有点，只对经过这个点的散块操作进行双指针，整块操作可以通过记录整块操作数量的前缀和来维护。于是复杂度为 \(\mathcal O(n\sqrt{n})\)。
P7897 [Ynoi2006] spxmcq
给定一棵以 \(1\) 为根的有根树，第 \(i\) 个节点权值为 \(a_i\)。有 \(m\) 次询问，每次将所有点权值增加 \(x\)，然后询问 \(u\) 子树内所有包含 \(u\) 的连通点集的权值和最大是多少。
\(n,m\le 10^6,|a_i|,|x_i|\le 10^8\)。
view solution
简要总结：树形DP遇到从 \(\max(0,f_v)\) 进行转移，可以考虑只从 \(f_v>0\) 的 \(v\) 向父亲连边，在形成的一棵森林中进行 DP。
根据题意容易写出转移方程，设 \(f_u\) 表示 \(u\) 子树内包含 \(u\) 的连通点集的最大权值和：
\(\max\) 非常恶心，我们考虑只连接满足 \(f_v>0\) 的点 \(v\) 到父亲的边，在形成的一棵森林中，转移式变为：
记 \(siz_u\) 为 \(u\) 的子树大小，\(sum_u\) 为 \(u\) 子树中所有点的 \(a\) 之和，那么有 \(f_u=xsiz_u+sum_u\)。可以 \(\mathcal O(1)\) 求解。
回答原问题，考虑如何维护这棵森林，注意到 \(f_u>0\) 等价于 \(x> \dfrac{-sum_u}{siz_u}\)，于是可以将所有询问离线下来按 \(x\) 从小到大排序，随着 \(x\) 的增大，不断将所有 \(x>\dfrac{-sum_u}{siz_u}\) 的 \(u\) 取出来，将 \(u\) 与原树父亲合并，并修改现在 \(u\) 所在树的根对应的阈值，对 \(u\) 的一段祖先的 \(siz_u\) 与 \(sum_u\) 进行修改。可以用 \(priority\_queue\) 维护所有阈值，将链加转化为单点加子树求和，即可 \(\mathcal O(n\log n)\) 使用树状数组完成。
CF1603E. A Perfect Problem
定义一个序列 \(b_1,b_2,b_3,\dots b_m\) 是好的，当且仅当 \(\min_{i=1}^{m}b_i\max_{i=1}^{m}b_i\ge \sum_{i=1}^{m}b_i\)。
询问有多少个长为 \(n\) 的序列 \(\{a_i\}\) 满足 \(1\le a_i\le n+1\)，且其所有子序列都是好的。
view solution
首先可以发现一个序列满足条件当且仅当将它从小到大排序后每个前缀都是好的。不妨设排序后的结果为 \(a_1,a_2,\dots a_n\)。可以直接对着这个判定方式设计一个 \(dp\) ，枚举 \(a_1\)，然后从小到大填入数字，\(f_{i,j,k}\) 表示已经填了 \(i\) 个数，总和为 \(j\)，正在考虑填入第 \(k\) 个数，据此可以得到一个状态数 \(\mathcal O(n^4)\)，转移 \(\mathcal O(n)\)，总复杂度为 \(\mathcal O(n^6)\) 的做法。
观察对前缀的限制，长为 \(i\) 的前缀满足条件就意味着 \(a_1a_i\ge \sum_{i=1}^{i}a_i\ge a_1i\)，因此有 \(a_i\ge i\)，同时如果取 \(a_i=i\) 则必须有 \(a_1=a_2=a_3=\dots=a_i=i\)。
记 \(b_i=a_i-a_1\)，枚举 \(a_1\)，则原限制变成了：
-
\(\sum_{i=1}^{n}b_i\le a_1\)
-
\(\forall i\in[a_1+1,n],i-a_1\le b_i\le n+1-a_1\)。
于是将 \(dp\) 改为从大到小填 \(b_i\)，有转移：
此时第二维 \(\sum b_i\) 变成了 \(\mathcal O(n)\) 的，因此转移总复杂度也就是 \(\sum_{i=1}^{n+1-a_1}\dfrac{a_1}{i}=\mathcal O(n\log n)\)，总复杂度 \(\mathcal O(n^4\sqrt{n}\log n)\)。
考虑优化，注意到当 \(a_1\le n-2\sqrt{n}\) 时，有 \(b_n\ge n-a_1\ge 2\sqrt{n},b_{n-1}\ge 2\sqrt{n}-1,\dots b_{n-\sqrt{n}}\ge \sqrt{n}\)，因此必然有 \(b_1+b_2+\dots b_n>a_1\)，答案为 \(0\) 可以不用考虑。据此可以进一步将复杂度优化到 \(\mathcal O(n^3\sqrt{n}\log n)\)。
CF1603D. Artistic Partition
定义函数 \(c(l,r)=\sum_{l\le i\le j\le r}[\gcd(i,j)\ge l]\)，再定义函数 \(f(n,k)\)，表示将 \(1\sim n\) 拆分成 \(k\) 段 \((x_1,x_2],(x_2,x_3],(x_3,x_4],\dots,(x_k,x_{k+1}]\)，满足 \(0=x_1<x_2<x_3<\dots<x_k<x_{k+1}=n\)，得到的 \(\sum_{i=1}^{k}c(x_i+1,x_{i+1})\) 的最小值。
\(T\) 次询问 \(f(n,k)\)。\(T\le 3\times 10^5,k\le n\le 10^5\)。
view solution
首先容易写出一个对 \(f\) 的暴力转移：
暴力实现这一过程，我们可以 \(\mathcal O(n^3)\) 预处理 \(c\)，再 \(\mathcal O(n^3)\) 进行转移。
考虑分别进行优化，对于 \(dp\) 转移的部分，\(\mathcal O(n^2)\) 的状态是我们无法承受的，考虑优化：
首先 \(c(l,r)\) 必定 \(\ge r-l+1\)，因为每一对 \((i,i)(l\le i\le r)\) 都会作出贡献。同时当 \(r\le 2l-1\) 时 \(c(l,r)\) 会取到下界 \(r-l+1\)。因此当 \(k\ge \log_2 n\) 时，一定存在一种方法将 \(1\sim n\) 拆分成 \(k\) 个满足 \(r\le 2l-1\) 的区间 \([l,r]\)，因此当 \(k\le \log_2 n\) 时 \(f_{n,k}=n\)，于是状态数被优化到了 \(\mathcal O(n\log n)\)。
对于预处理 \(c\) 的部分，考虑推柿子：
于是通过预处理 \(\varphi\) 的前缀和 \(s(i)=\sum_{j\le i}\varphi(j)\) ，有 \(c(l,r)=\sum_{g=l}^{r}s(r/g)\)，可以通过整除分块做到 \(\mathcal O(\sqrt{r-l})\) 进行依次查询，也可以 \(\mathcal O(n\sqrt{n})\) 预处理后 \(\mathcal O(1)\) 查询。
求 \(c\) 的复杂度已经可以承受了，回到 \(dp\) 转移的部分，这个 \(dp\) 显然无法单调队列/斜率优化/数据结构优化，于是考虑决策单调性优化，大胆猜测 \(c(l,r)\) 满足四边形不等式，事实上确实如此，证明如下：
设 \(l_1\le l_2\le r_1\le r_2\) ，有：
于是我们可以用分治做法优化 \(dp\) ，将 \(dp\) 转移优化到 \(\mathcal O(n\log^2 n)\)，最终总复杂度为 \(\mathcal O(n\log^2n+n\sqrt{n})\)。
当然也可以不用预处理 \(c\)，在分治的过程中在 \([ql,qr]\) 里找 \(mid\) 的决策点时，可以先 \(\mathcal O(\sqrt{r-l})\) 求出 \(c(qr+1,mid)\)，然后就可以容易的递推出其他决策点对应的 \(c\)，复杂度依然正确。
CF1592F1/F2 Alice and Recoloring
view F1 solution
首先翻转包含 \((n,1)\) 与 \((1,m)\) 所在矩形的操作可以用两个包含矩形 \((1,1)\) 的操作实现，因此我们可以忽略这两个操作。将矩阵进行二维差分，那么包含 \((1,1)\) 矩形的操作等价于单点修改，包含 \((n,m)\) 矩形的操作等价于同时修改 \((i,j),(n,j),(i,m),(n,m)\) 的颜色。因为后一种操作本身会有 \(4\) 的代价，那么这个操作只会在这四个点颜色都是 \(1\) 的时候才会操作，并且只会执行一次，直接 \(\mathcal O(nm)\) 遍历一遍判断是否有这样的 \((i,j)\) 即可。
view F2 solution
唯一的区别是对右下角矩形的操作代价变成了 \(2\)。那么此时如果对点 \((i,j)\) 进行操作，我们必须保证 \((i,j),(n,j),(i,m)\) 都是 \(1\)，因此每一行每一列最多只有一个点被选中作为操作矩形的左上端点。因此以行作为左部点，列作为右部点跑二分图匹配即可。
CF1495E Qingshan and Daniel
一个环上有 \(n\) 个人分属两个阵营，每个人手上有两张牌。一开始第一个人打出一张牌，随后它右侧最近的与它不同阵营且有牌的人会打出一张牌以响应它，随后它右侧的不同阵营的人会继续响应。。。当无人能出牌时游戏停止。问最终每人出了多少张牌？\(n\le 5\times 10^6\)。
view solution
考虑游戏结束一定是手牌较少的一方所有人都出完了牌，不妨假设手牌较少的是 \(A\) 阵营，另一个是 \(B\) 阵营，那么出牌的过程一定是 \(ABABABAB\dots\) 或者 \(BABABABA\dots\)，如果是后者，我们可以让第一个人先出一张牌，将响应它的人看作第一个人就转化成了第一种出牌过程。
在 \(ABABABAB\) 的出牌过程中，可以大胆猜测 \(A\) 阵营的出牌顺序与最终每人出的牌数量没有任何关系。
证明考虑交换 \(A\) 中相邻的两次出牌的顺序，不妨设它们是由 \(A_1、A_2\) 出的牌，由 \(B_1、B_2\) 响应。若 \(B_1=B_2\) 那么显然不会有影响；否则意味着 \(B_1\) 出了自己的最后一张牌，如果 \(A_2\) 也在 \(B_1\) 前面，那么 \(B_1\) 响应 \(A_2\)，\(B_2\) 响应 \(A_1\)，否则在 \(B_1\) 会一直保留着自己的最后一张牌给 \(A_1\)，不会产生影响，由此得证。
因此，可以假设 \(A\) 阵营是从左到右依次出牌的，这样就只需要维护一个 \(s\) 表示目前还没有被响应的 \(A\) 阵营牌数量，然后扫一遍环即可。
CF1572F Stations
一条大街上有 \(n\) 座大楼，从左至右第 \(i\) 座大楼标号为 \(i\)，有高度 \(h_i\) 与参数 \(w_i\)。楼 \(i\) 能看到 \(j\) 当且仅当 \(j\in [i,w_i]\) 且 \(\forall k\in[i+1,j],h_k<h_i\)。初始对任意的 \(i\) 有 \(h_i=0,w_i=i\)，现在先后执行 \(q\) 次操作，操作有两种：
- \(1\ x\ y\)：重建大楼 \(x\) 使它比所有其他大楼都高，且 \(w_x=y\)。
- \(2\ l\ r\)：令 \(b_i\) 表示能看到大楼 \(i\) 的大楼数量，求 \(\sum_{i=l}^{r}b_i\)。
\(n,q\le 2\times 10^5\)。
view solution
直接维护 \(b\) 非常困难，考虑维护 \(r_i\) 表示从楼 \(i\) 能看到的最靠右的大楼，那么初始所有 \(r_i=i\)，修改 \(1\ x\ y\) 相当于单点修改 \(r_x=y\)，并且对 \(i\in [1,x-1]\) 令 \(r_i=\min(r_i,x-1)\)。
于是可以用 segment tree beats 维护 \(r\)，每次只会将一些 \(r\) 相同的点的 \(r\) 同时减小到相同值，这可以通过依次对 \(b\) 的区间修改 \(\mathcal O(\log n)\) 维护，segment tree beats 会产生 \(\mathcal O((n+q)\log n)\) 次操作，于是总复杂度为 \(\mathcal O((n+q)\log^2n)\)。
CF1534G A New Beginning
在一个二维直角坐标系上有 \(n\) 个点，第 \(i\) 个点为 \((x_i,y_i)\) ，你初始在 \((0,0)\)，可以不花费任何代价向上或向右移动任意长度。现在你想要在移动过程中摧毁这 \(n\) 个点（顺序随意），在点 \((x,y)\) 摧毁点 \((x_i,y_i)\) 需要花费 \(\max(|x-x_i|,|y-y_i|)\) 的能量，问最少少花费多少能量才能摧毁所有点。\(n\le 8\times 10^5,0\le x_i,y_i\le 10^9\)。
view solution
题目中的距离是切比雪夫距离，是一个难以处理的点，但是不难发现，一定存在一个方案使得对于任意一个点 \(i\) ，在路径上摧毁它的点在 \(x+y=x_i+y_i\) 上。
证明考虑设最终摧毁它花费的代价为 \(t\)，那么一定是在以 \((x_i,y_i)\) 为边界的一个边长为 \(2t\) 正方形的边界上进行的摧毁。
考虑移动过程中抵达这个正方形的位置，显然这个位置不可能是右边界或上边界。如果是下边界，那么下一步不可能是向上（这样向上一步再摧毁代价就变成 \(t-1\) 了），而只能一直向右到达右下端点，走到左边界同理只能一直向上到达左上端点。因此，一定存在方案是在这条对角线上完成的摧毁。
接下来考虑将每个点按 \(x+y\) 的大小排序分层，可以按照层进行 \(dp\)，设 \(dp_{i,j}\) 表示走到第 \(i\) 层时 \(x=j\) 的最小代价，转移考虑枚举上一层的 \(x\) 坐标：
直接 \(dp\) 复杂度还是太高，由于每次转移新增的 \(|x-x_i|\) 是一个下凸的函数，那么将 \(dp_{i,x}\) 看作关于 \(x\) 的函数 \(dp_i(x)\)，这个函数也是一个下凸函数。
接下来就可以使用经典技巧：用数据结构维护凸函数。在本题中，每次转移只会增加 \(\pm 1\) 的斜率，因此可以直接维护 \(dp\) 函数的每个斜率增加 \(1\) 的位置，并维护斜率为 \(0\) 的区间。那么最优解一定在斜率为 \(0\) 处取到。
转移时，在 \([x-\Delta,x]\) 区间取 \(\min\) 进行转移，相当于将斜率为 \(0\) 的部分向右拉长 \(\Delta\) 的距离，并且斜率 \(>0\) 的函数同时向右平移 \(\Delta\)，于是我们直接维护目前向右移动的距离，并用两个堆分别维护斜率 \(<0\) 与 \(>0\) 的部分斜率的变化点。
加入 \(|x-x_i|\) 时，这会导致 \(x_i\) 左侧斜率 \(-1\)，右侧斜率 \(+1\)，因此需要在 \(x_i\) 处增加两个变化点，对于最低点的变化，则根据 \(x_i\) 于最低点的大小关系分三类讨论即可，具体参见代码。
CF1466H Finding satisfactory solutions
有 \(n\) 个人与 \(n\) 样物品，每个人选择了一样物品，同时第 \(i\) 个人对这 \(n\) 样物品有一个好感度的排行，按好感度从大到小一次为 \(\{s_{i,1},s_{i,2},\dots,s_{i,n}\}\)（\(i\in [0,n]\)）。
如果存在这 \(n\) 个人的一个子集 \(s\) ，使得可以对 \(s\) 内的人的物品进行一次交换，使：
- 不存在任何一个人交换得到了一个更不喜欢的物品。
- 存在至少一个人得到了一个更喜欢的物品。
那么就认为当前物品的分配方案是不好的，否则是好的。
现在给出了一种物品分配方案 \(\{a_n\}\)，问有多少组 \(\{\{s_{1,n}\},\{s_{2,n}\},\dots,\{s_{n,n}\}\}\) 使得这一分配方案是好的。
\(n\le 40\)。
view solution
考虑如果 \(i\) 比起 \(a_i\) 来更喜欢 \(j\)，就从 \(i\) 向 \(j\) 连一条白边，再对每个 \(i\) 从 \(i\) 向 \(a_i\) 连一条黑边，那么 \(\{a_n\}\) 是好的意味着这张图不存在一个包含白边的环。
涉及到环，考虑缩点，那么环一定在某个强连通分量内产生。因此，如果某个强连通分量中包含白色边，那么一定可以在该强连通分量中找到一个包含白边的环，于是我们希望所有强连通分量都只有黑边构成。
注意到黑边是哪些是确定的，因此我们对这些黑边进行缩点，事实上最终的强连通分量就是目前缩点得到的强连通分量，白边只能在它们之间连接。当然，由于黑边中每个点的度数都是 \(2\) ，缩点其实得到的就是 \(\{a_n\}\) 排列中的环。问题转化为给定一些点，在它们之间连边得到一个 \(DAG\)。
当然由于本题是选排列而不是连边，因此某一个点连出 \(j\) 条边意味着排列有 \(j!(n-1-j)!\) 中选择方案。
考虑状压 \(DP\)，设 \(f_s\) 表示对 \(s\) 内部的点组成 \(DAG\) 的方案。这是一个经典套路，可以枚举 \(s\) 中入度为 \(0\) 的点集 \(T\)，计算 \(T\) 向 \(S/T\) 连边的方案数（记为 \(g_{T,S/T}\)），从 \(f_{S/T}\) 转移过来。
但有可能 \(S/T\) 的部分中也有入度为 \(0\) 的点，需要容斥枚举实际上入度为 \(0\) 的点集 \(P\)，有：
由于
于是
暴力枚举子集进行 \(DP\) 复杂度依然太高，注意到 \(S\) 中大小相同的环的贡献是一样的，因此可以将 \(S\) 改为所有不同长度的环的数量，这样一来状态数大大优化，据官方题解应该是 \(\mathcal O(P(n)n^3)\) 的，其中 \(P(n)\) 是 \(n\) 的拆分数，可以通过此题。
