[POI2005]PRA-Dextrogyrate Camel 【DP】【计算几何】

洛谷P3433

Description

平面上有 \(n\) 个点 \((x_i,y_i)\)。小 \(L\) 从 \(1\) 号点出发，面向 \(2\) 号点以直线前进。每到达一个点，小 \(L\) 就可以让前进方向顺时针旋转 \([0,180)\) 度，并向下一个点以直线前进，最终回到 \(1\) 号店。要求在整个行进过程中路径不相交（不包括顶点处），不重复经过 \(1\) 号点外的点，到达 \(1\) 号点后立即结束，请问小 \(L\) 最多能一次经过多少个节点？数据保证无三点共线。

\(n\le 2000,|x_i|,|y_i|\le 16000\)。

Solution

首先平移坐标系，使 \(1\) 号点为原点。

考虑什么样的路径是合法的：（此处借用了这位大佬题解中的图片）

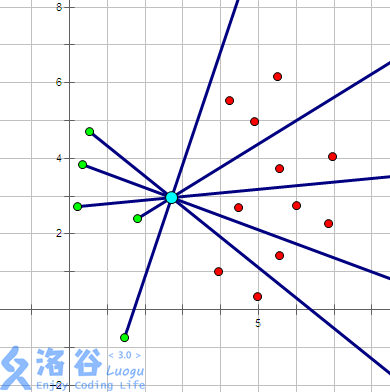
图中的蓝色点为 \(1\) 号点，红色与绿色为其他点，当选择了某个红色点时，其上方的所有红色点都无法再走到了；同样的，选择了某个绿色点时，其下方的所有绿色点也无法走到了。

因此，将 \(1\) 号点外的点极角排序，那么最优选择一定时从 \(2\) 号点开始沿顺时针方向走（此时合法的目标点一定再顺时针方向）。因此可以极角排序后，将 \(2\) 号点排在首位，其他点按顺时针方向依次加入。设 \(dp_{i,j}\) 表示现在走到了第 \(i\) 个点，上一个走到的点位 \(j\) 号点时的最长路径。然后 \(\mathcal O(n)\) 枚举下一个转移点并判断能否到达。状态是 \(\mathcal O(n^2)\) 的，因此总复杂度位 \(\mathcal O(n^3)\)。

考虑优化，将 \(dp_{i,j}\) 改为走到了第 \(i\) 个点，经过了 \(\ge j\) 个点时能使得可选择后继范围最大的前驱。那么转移时，枚举当前点 \(i\) 以及前驱 \(j\)，即可二分找到能够从 \(j\) 到达 \(i\) 的前提下，经过的路径最大是多少，如果二分出的答案是 \(k\)，就可以用 \(dp_{j,k}\) 更新 \(dp_{i,k+1}\)。更新完之后，再对与每个 \(i\) ，将 \(j\) 从大到小扫一遍，用 \(dp_{i,j}\) 更新 \(dp_{i,j-1}\) 选择可选后继范围更大的一个前驱。判断谁的可选范围最大可以使用叉积完成。

最终复杂度优化到 \(\mathcal O(n^2\log n)\)。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2010;
const double pi=acos(-1.0);
int n,pos[N],dp[N][N];
double ang[N];
struct pt{
	int x,y;
	pt(int _x=0,int _y=0){x=_x;y=_y;}
}p[N];
inline ll operator ^(const pt& a,const pt& b){return 1ll*a.x*b.y-1ll*a.y*b.x;}
inline pt operator -(const pt& a,const pt& b){return pt(a.x-b.x,a.y-b.y);}
inline bool cmp(int x,int y){return ang[x]<ang[y];}
inline bool check(int i,int j,int k){return ((p[pos[j]]-p[pos[i]])^(p[pos[k]]-p[pos[j]]))<0;}
inline void upd(int pos,int &x,int y){
	if(x==-1){x=y;return ;}
	(check(pos,y,x))&&(x=y);
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i) scanf("%d%d",&p[i].x,&p[i].y);
	for(int i=2;i<=n;++i) p[i]=p[i]-p[1];p[1]=p[1]-p[1];
	for(int i=0;i<n;++i) pos[i]=i+1,ang[i+1]=atan2(p[i+1].y,p[i+1].x);
	double tmp=ang[2];
	for(int i=2;i<=n;++i){
		ang[i]=tmp-ang[i];
		ang[i]=fmod(ang[i]+6*pi,2*pi);
	}
	sort(pos+1,pos+n,cmp);
	memset(dp,-1,sizeof(dp));
	dp[1][1]=0;
	int ans=1;
	for(int i=2;i<n;++i){
		for(int j=1;j<i;++j){
			if(check(j,i,0)){
				int l=1,r=j,ret=-1;
				while(l<=r){
					int mid=(l+r)>>1;
					if((~dp[j][mid])&&check(dp[j][mid],j,i)) l=mid+1,ret=mid;
					else r=mid-1;
				}
				if(~ret) upd(i,dp[i][ret+1],j),ans=max(ans,ret+1);
			}
		}
		for(int j=i-1;~j;--j) if(~dp[i][j+1]) upd(i,dp[i][j],dp[i][j+1]);
	}
	printf("%d\n",ans);
	return 0;
}