后缀自动机学习笔记

本篇博客部分内容及图片引用自KesdiaelKen的博客

一·、概述

后缀自动机(suffix automaton,SAM)是一个能够解决许多字符串问题的自动机。它可以说是常考的字符串算法中最困难的一个，解决的问题也非常多。

想要学会SAM，首先得先学会\(trie\)，较高深的内容也需要后缀数组SA相关的知识。

后缀自动机，实质上就是一种用一个DAG表示一个字符串的所有子串的方法，表示一个字符串所有子串的方法我们并不是没有学过，那就是\(trie\)：即将原串的所有后缀都加入\(trie\)树中，得到的\(trie\)树存在一个根以及若干终止点，满足重要性质：

• 从根到任意节点的任意路径对应原串的一个子串，原串的每个子串对应从根开始的某条路径。
• 从根到任意终止节点的任意路径对应原串的一个后缀

但是，\(trie\)树的节点数达到了\(\mathcal O(n^2)\)的级别，这是我们不能接受的，我们需要一种更好的表示所有子串信息的方法，这就是SAM了。

以下的所有内容中我们都认为原字符串为\(s\)。

SAM是一个能识别\(s\)的所有后缀的最小DFA，不理解什么是DFA也没关系，总之就是它满足以下性质：

• SAM是一个DAG，节点被称为状态，边被称为转移，每个转移上标有一些字母
• 存在一个初始状态，从初始状态出发能到达任意节点，并且将从初始状态出发的任意路径上的所有转移的字母写下来就是\(s\)的一个子串，\(s\)的每一个子串均能被这样的路径表示出来
• 存在若干个终止状态，从初始状态到终止状态的任意路径都是\(s\)的一个后缀，\(s\)的每一个后缀都可以由这样的方式表示出来。
• SAM的状态数、转移数都是线性的

二、SAM的结构

首先，我们引入一个新定义：结束位置\(endpos\)，对于字符串\(s\)的任意子串\(t\)，\(endpos(t)\)表示\(t\)在\(s\)中的所有结束位置组成的集合，例如对于\(s=“dabda”,endpos(“da”)=\{2,5\},endpos(“b”)=\{3\}\)。

\(endpos\)满足许多很好的性质，这是SAM的关键：

引理1：对于字符串的任意非空子串\(u\)与\(v\)，如果\(endpos(u)=endpos(v)\)，且\(|u|\le|v|\)，那么\(u\)是\(v\)的后缀。

证明：还是比较显然的。

引理2：对于字符串的任意非空子串\(u\)与\(v\)，如果\(|u|\le|v|\)，那么\(endpos(v)\in endpos(u)\)或者$endpos(u)\cap endpos(v)=\varnothing $。

证明：如果\(u\)是\(v\)的后缀，那么\(v\)出现时\(u\)一定出现，于是\(endpos(v)\in endpos(u)\)，否则\(u\)与\(v\)一定不会同时出现。

于是我们按照不同的\(endpos\)将原串的所有子串分为若干个\(endpos\)等价类。

引理3：对于任意一个\(endpos\)等价类，其中的所有子串将它们按长度从大到小排序，那么每一个子串都是前一个子串的后缀，长度\(=\)前者\(-1\)，等价类的长度值域恰好覆盖连续的一段。

证明：如果等价类仅包含一个字符串那么引理显然成立，否则设\(u\)为该等价类最短的字符串，\(v\)为最长的字符串，那么\(v\)的所有长度\(\ge |u|\)的后缀，根据引理\(1\)，它们也一定属于这一等价类中。

对于任意一个等价类，我们设\(v\)为该等价类最长的子串，那么在\(v\)前加另一个字符，如果依然得到原串的子串，那么它一定属于另一个等价类，并且由引理2，这个等价类的\(endpos\)一定\(\in endpos(v)\)，并且在\(v\)前加不同的字符会得到不同的等价类，它们的\(endpos\)一定不相交，于是我们相当于将\(endpos(v)\)拆分为了若干个新的集合并保留原来的集合。我们将从\(A\)分割得到\(B\)看作是父子关系，借此我们就能建出一棵树：

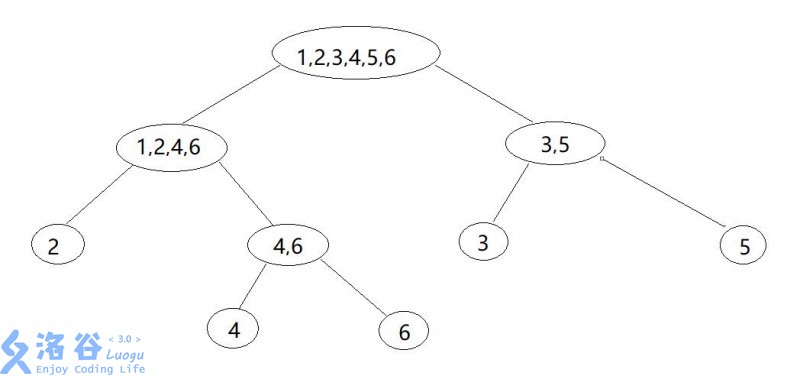
这是以\(aababa\)为例建出的树，图片来自开头提到的博客。

通过这样的例子，根据分割关系显然可以发现树的节点个数是不超过\(\mathcal O(2|s|)\)的，这棵树我们称之为\(parent\ tree\)。我们将基于\(parent\ tree\)来建出SAM，所有\(endpos\)等价类就是SAM中的节点，根就是SAM的初始节点。

我们认为任意等价类\(x\)中的最长字符串的长度为\(len(x)\)，最短字符串长度为\(minlen(x)\)，它在\(parent\ tree\)上的父亲为\(link(x)\)，那么显然有\(minlen(x)=len(link(x))+1\)，因为\(x\)正是由\(link(x)\)增加一个字符得来的。

但SAM的转移并不是\(parent\ tree\)上的边，因为这些边是在字符串前面加一个字符，而SAM中的转移边应该是在最后加一个字符，我们希望能在\(parent\ tree\)的节点之间连边，使起点出发到任意点的路径都对应属于该点的一个字符串。

具体建出来的结果是这样的：

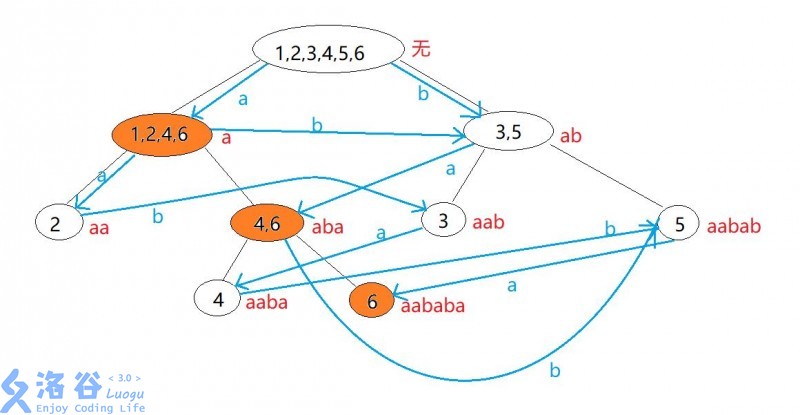
接下来，我们将介绍如何在线性时间内建出SAM:

三、SAM的构造

和PAM一样，我们也采用增量法构造SAM，即依次将\(s\)的每一个字母加入SAM中并使SAM维护新出现的子串。

我们记录\(c\)为要加入的这个字母，它是第\(i\)个字母，\(last\)为旧串对应的节点编号，用\(ch[i][c]\)表示\(i\)的各条转移连向的点，设\(1\)为初始节点。

• 首先，我们新建一个节点\(cur\)表示新串，显然它的\(endpos=\{i\}\)是全新的，应该是一个新的节点，有\(len[cur]=len[last]+1\)

  int cur=++tot;len[cur]=len[last]+1;
  

• 接下来我们考虑哪些子串的\(endpos\)需要被修改——新串的后缀，它们都是原串的一个后缀通过转移\(c\)得来的，我们通过遍历原串的后缀来找到它们，遍历后缀的方法则是从\(last\)出发，不断让\(last=link[last]\)直至\(last=1\)即根节点，这个结合\(link\)的含义不难发现。

• 显然我们是按后缀的长度从大到小遍历的，一开始的几个后缀可能没有\(c\)这个转移，也就是说它们对应的新串后缀从未在旧串中出现过，因此它们的\(endpos=\{i\}\)，应该属于\(cur\)：

  while(p&&!ch[p][c]){//p=0表明我们已经遍历完所有后缀了
  	ch[p][c]=cur;
  	p=link[p];	
  }
  if(!p) link[cur]=1;
  

• 如果\(p=0\)，那么所有新串后缀都已并入\(cur\)，这样的节点在\(parent\ tree\)上只能从初始节点转移而来了，因此将\(link[cur]\)设为\(1\)。

• 假设现在来到了节点\(p\)，\(ch[p][c]=q\)是已经出现过的子串，它的\(endpos\)应该增加一个\({i}\)进去，如果\(q\)中只有这一个子串，也就是说\(len[q]=len[p]+1\)，于是\(q\)中最长的串都是新串的后缀，所以\(q\)中所有串均为新串的后缀，\(endpos\)都要增加一个\(i\)，于是我们不用修改它，因为\(cur\)就是\(q\)前加一个字母得到的，我们将\(link[cur]\)指向\(q\)即可。

  int q=ch[p][c];
  if(len[q]==len[p]+1) link[cur]=q;
  

• 否则，意味着我们要将\(q\)中代表新串后缀的子串提出来修改它们的\(endpos\)，于是我们新建一个\(np\)表示这些子串的\(endpos\)，那么\(np\)中的最长字符串是新串的后缀，它的所有后缀都是新串的后缀，因此\(np\)中的字符串一定是\(q\)中最短的一些字符串。于是\(len[np]=len[p]+1\)，且\(np\)的\(ch\)数组应当与\(q\)相同。考虑\(link[np]\)，之前的\(link[q]\)表示什么？表示\(link[q]\)通过加一个字符得到了\(q\)中最短的一个子串，这个子串一定属于\(np\)，于是\(link[np]=link[q]\)，\(link[q]\)自然就应该更换为\(np\)，\(link[cur]\)也应该指向\(np\)

• 拆分完后，我们不仅要考虑\(q\)与\(np\)的转移，还要考虑原先连向\(np\)与\(q\)的转移，原先在字符串最后增加一个字符能得到\(np\)的点，我们要将它们的转移边改为连向\(np\)，然后我们继续跳\(link[p]\)，接下来的点也应该在\(endpos\)中增加\(i\)，而如果它们本来连向的是\(q\)，那么直接改为连向\(np\)，当\(ch[p][c]\not=q\)时，意味着现在\(p\)连向的是\(q\)的祖先了，\(q\)的父亲\(np\)的\(endpos\)中已经包含\(i\)了，因此我们就不需要再修改它们了。

  else{
  	int np=++tot;
  	len[np]=len[p]+1;
  	link[np]=link[q];
  	ch[np]=ch[q];//实际上ch[np]作为一个数组它不能这么用，我们这里只是表示这个意思
  	while(p&&ch[p][c]==q){
  		ch[p][c]=np;
  		p=link[p];
  	}
  	link[cur]=link[q]=np;
  }
  

• 最后将\(last\)更新为\(cur\)，我们就完成了整个构造的过程。依次加入每个字符，我们就完成了SAM的构造：

• 完整代码如下：代码中也有一些注释，不过我认为我前面的讲解会更好理解一些。

  inline void insert(int c){
  	int cur=++tot;
  	len[cur]=len[last]+1;//开新节点 
  	int p=last;
  	while(p&&(!ch[p][c])){
  		ch[p][c]=cur;
  		p=link[p];
  	}//原s的所有后缀都应启动新转移c 
  	if(!p) link[cur]=0;//c没出现过，直接连向初始状态 
  	else{
  		int q=ch[p][c];
  		if(len[q]==len[p]+1) link[cur]=q;//是连续的则直接link 
  		else{
  			int np=++tot;
  			len[np]=len[p]+1;
  			link[np]=link[q];
  			ch[np]=ch[q]//否则将状态q分成两部分q与np，让q连向np 
  			while(p!=-1&&ch[p][c]==q){
  				ch[p][c]=np;
  				p=link[p];
  			}//修改所有连向q的转移 
  			link[q]=link[cur]=np;
  		}
  	}
  	siz[cur]=1;
  	last=cur;//更新last 
  }
  

  还有一个问题，为什么这样的构造复杂度是正确的？

  四、复杂度证明

  首先我们先证明SAM的状态数与转移数是\(\mathcal O(n)\)的，状态数我们通过\(parent\ tree\)已经证明，接下来考虑转移数：

  • 我们先找出SAM的一个生成树，将其他边舍去，然后我们从每一个后缀对应的终止状态出发沿SAM上起始状态到它的路径(这个是唯一的)往起始状态跑，然后如果遇见了一条非树边，就把这条边加入SAM中，然后沿这条边到达点\(u\)，然后我们这个时候不走之前的路径了，改沿生成树上\(u\)到起点的路径跑回起点。这样的一条路径得到的字符串不一定是这个后缀，但它依然是从初始状态到终止状态的一条边，对应的也是一个后缀，并且没有被跑过(不然不会现在才连上)

  • 此时，我们将这个后缀划掉不跑了，继续回到\(u\)跑之前的后缀，重复这样的流程。

  • 整个流程中，我们每增加的一条非树边都唯一对应一个后缀，因此非树边的数量是\(\mathcal O(n)\)的，而树边数量等于状态数也是\(\mathcal O(n)\)的，因此总转移数是\(\mathcal O(n)\)的。

  回来考虑构造的复杂度：构造中看起来不是线性的应该就是以下几部分：

• 遍历旧串后缀，增加到\(cur\)的转移

• 增加新节点后复制之前\(q\)的转移到\(np\)上去(\(ch[np]=ch[q]\))

• 修改之前到\(q\)的转移到\(np\)上

  对于前两个，它们每操作一次，就意味着新增一条转移，因此总复杂度是\(\mathcal O(n)\)的，(补充一点：字符集较大时我们用\(unordered\_map\)维护\(ch\)这样每次取出会带有一些常数，较小时(大部分情况下)我们直接把\(ch\)开为数组暴力转移)

  对于第三个，我们修改的转移就是连向新节点的所有转移，这个新节点不会再被操作三遍历到了，因此每条边最多只会被修改一次，操作三的总复杂度依然是线性的。

  至此，我们就证明了后缀自动机构造的线性复杂度。

五、应用及例题

本篇博客篇幅已经很大了，所以这部分我们下篇博客再说(咕咕咕)