快速傅里叶变换FFT
多项式
顾名思义,一个最高次数为\(n-1\)的多项式共有\(n\)项分别为\(0,1,2,\dots,n-1\)
多项式的系数表示法
多项式的点值表示法
一个最高次数为\(n-1\)的多项式可以有\(n\)个点值唯一确定,
因此我们代入\(n\)个不同的数\(a_0,a_1,\dots,a_{n-1}\),得到对应的点值,即可以此来表示多项式
多项式的四则运算
我们现在来考虑多项式的四则运算:
加减显然可以直接 \(\mathcal O(n)\) 做,那么乘呢?
系数表示法相乘的复杂度为\,而点值表示法相乘就很容易了,可以直接\(\mathcal O(n)\)做。
即将两个用点值表示法表示的多项式\(f\)与\(g\)的每一个点值依次相乘。
遗憾的是,大部分情况下我们都会使用系数表示法来表示多项式,因此我们需要一个能够快速在系数表示法与点值表示法之间相互转化的方法。
傅里叶为我们带来了一种:
快速傅里叶变换FFT
首先考虑将系数转化为点值:
直观的想法是随机代入\(n\)个数,复杂度为\(O(n^2)\)
但是考虑一下:如果你代入数中存在的\(i,j\)满足\(a_j=2a_i\),那么我们代入计算的时候是否会简单一些?
仔细想一想会发现其实不行,但这确实为我们提供了一种思路:用一些能使运算简便的特殊的数来代入计算:
于是我们就有了
单位根
对于任意的数\(n\),它对应的单位根是满足:
的所有\(x\)。
这样的\(x\)在实数范围内只有\(2\)个,但在复数范围内有\(n\)个,我们认为他们是\(w_n^i,i=0,1,2,\dots,n-1\)
为什么单位根可以简化运算呢?
考虑一个以复数的实部为\(x\)轴,虚部为\(y\)轴的平面直角坐标系,并作出一个单位圆(以原点为圆心,半径为1)

单位根\(w_n^i\)就是将这个圆\(n\)等分后,从\(x\)轴正半轴上开始数,经过\(i\)个扇形后到达的一个与圆的交点:
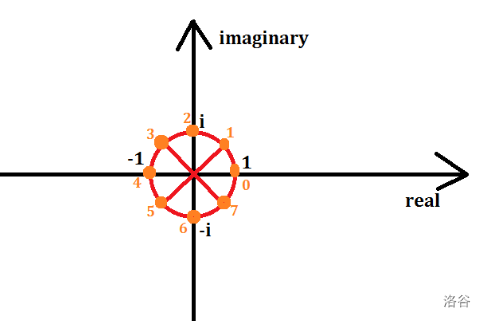
以\(w_n^1\)为例(一般也可简写为\(w_n\)),它的\(n\)次方,就相当于它所对应的角度乘上\(n\)倍,所得到的角度一定是\(2\pi\)的倍数,与\(x\)轴重合
根据单位圆的基本性质,我们就有了:
根据这个单位圆,我们可以推出单位根的一些性质:
现在我们进入正题:(为了方便,下文中的\(n\)都是2的幂)
我们要求的是
即
令
那么
我们将单位根\(w_n^k(k<\frac n2)\)代入得到:
再将\(w_n^{k+\frac n2}\)代入的到:
于是我们惊人地发现,只需要知道\(w_{\frac n2}^k\)代入\(A,B\)的点值,我们就可以得到\(w_n^k\)代入\(f\)的点值
于是我们就可以递归处理\(\frac n2\),易知这样做是\(\mathcal O(nlogn)\)的
但是递归的常数非常大,因为每一层递归相当于偶数项和奇数项分开递归下去,于是我们考虑每个系数最后所在的位置。
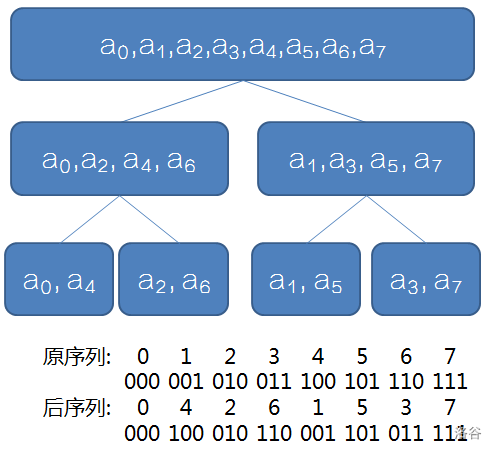
发现了吧:交换后序列的任意一项的系数的下标是交换前序列下标二进制下翻转后的结果。
而二进制下翻转后的结果,我们可以通过
int lim=1,len=0;
while(lim<(n+m)) lim<<=1,len++;//将答案的长度转换为2的次幂方便计算
for(int i=0;i<lim;++i) r[i]=(r[i>>1]>>1)|((i&1)<<(len-1));
求出
接下来,我们可以就可以一层一层向上迭代来完成系数表示法转点值表示法了:
struct pt{
double x,y;
pt(double _x=0,double _y=0){x=_x;y=_y;}
};
inline pt operator +(pt a,pt b){return pt(a.x+b.x,a.y+b.y);}
inline pt operator -(pt a,pt b){return pt(a.x-b.x,a.y-b.y);}
inline pt operator *(pt a,pt b){return pt(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
const double pi=acos(-1.0);
inline poly FFT(int lim,poly f,int tp){
for(int i=0;i<lim;++i) if(i<r[i]) swap(f[i],f[r[i]]);
for(int mid=1;mid<lim;mid<<=1){
int len=mid<<1;
pt wn=pt(cos(pi/mid),tp*sin(pi/mid));
for(int l=0;l+len-1<lim;l+=len){
pt w=pt(1,0);
for(int k=l;k<=l+mid-1;++k,w=w*wn){
pt w1=f[k],w2=f[k+mid];
f[k]=w1+w*w2;f[k+mid]=w1-w*w2;
}
}
}
return f;
}
IDFT傅里叶逆变换
接下来我们考虑将点值表示法转换为系数表示法:
考虑我们已经求出了\(f*g\)得到的\(h\)在\(w_n^0,w_n^1,\dots,w_n^{n-1}\)处的\(n\)个点值,我们设为\(y_0,y_1,\dots,y_{n-1}\),想要求出\(h\)的系数\(h_i\)
我们以\(y\)作为系数写出一个新的函数\(C\):
那么将\(y_i\)对应的值代入得到:
我们将\(w_n^0,w_n^{-1},w_n^{-2},\dots,w_n^{-(n-1)}\)代入进去试试?
即
交换和式得到:
我们令
那么
二式相减得
因此,当\(w_n^x-1\not=0\)时,该式就等于\(0\),只有当\(x=0\)时,\(w_n^x-1=0\),此时\(S(x)=\sum_{i=0}^{n-1}1^i=n\)
回到原式我们就有了
于是我们只需要到函数\(C(x)\)求出它在\(w_n^0,w_n^{-1},w_n^{-2},\dots,w_n^{-(n-1)}\)出的点值,再除以\(n\)就是\(h(x)\)的系数了。
代码如下,可以通过
模板题
#include<bits/stdc++.h>
using namespace std;
const int N=(1<<21)+20;
struct pt{
double x,y;
pt(double _x=0,double _y=0){x=_x;y=_y;}
}a[N],b[N];
pt operator +(pt a,pt b){return pt(a.x+b.x,a.y+b.y);}
pt operator -(pt a,pt b){return pt(a.x-b.x,a.y-b.y);}
pt operator *(pt a,pt b){return pt(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
const double pi=acos(-1.0);
void FFT(int lim,pt *a,int tp){
if(lim==1) return ;
int nlim=lim>>1;
pt a1[nlim+1],a2[nlim+1];
for(int i=0;i<=lim;i+=2) a1[i>>1]=a[i],a2[i>>1]=a[i+1];
FFT(nlim,a1,tp);FFT(nlim,a2,tp);
pt wn=pt(cos(2.0*pi/lim),tp*sin(2.0*pi/lim)),w=pt(1,0);//tp=-1时表示是IDFT,此时我们需要求的是(w_n^{-k})的点值
for(int i=0;i<nlim;++i,w=w*wn){
a[i]=a1[i]+w*a2[i];
a[i+nlim]=a1[i]-w*a2[i];
}
}
int main(){
int n,m,lim=1;
scanf("%d%d",&n,&m);
for(int i=0;i<=n;++i) scanf("%lf",&a[i].x);
for(int i=0;i<=m;++i) scanf("%lf",&b[i].x);
while(lim<=n+m) lim<<=1;
FFT(lim,a,1);
FFT(lim,b,1);
for(int i=0;i<=lim;++i) a[i]=a[i]*b[i];
FFT(lim,a,-1);
for(int i=0;i<=n+m;++i) printf("%.0lf ",(a[i].x+0.5)/lim);//注意精度问题
return 0;
}
\(FFT\)固然是解决多项式乘法的利器,但它有致命的缺陷————精度容易爆炸且无法取模,毕竟它是基于复数的运算的,
于是,我们有了更好的解决多项式乘法的办法————NTT


