只有2-SAT不是NPC呢——2-SAT学习笔记
什么是2-SAT?
我们举一个简单的例子:
机房里有三位大佬小s,小l,小m和一个蒟蒻tqr,他们刷题时有不同的要求(因为蒟蒻什么题都不会做,故不列举):
| 大佬/要求 | 小s | 小l | 小m |
|---|---|---|---|
| 要求1 | 不包含数论知识(¬a) | 包含数论知识(a) | 不包含数论知识(¬a) |
| 要求2 | 包含几何知识(b) | 包含几何知识(b) | 不包含几何知识(¬b) |
| 要求3 | 不包含图论知识(¬c) | 不包含图论知识(¬c) | 包含图论知识(c) |
在此之前,复习一下前置数学知识:
对于一个命题:如果a,那么b
其逆命题为:如果b,那么a
其否命题为:如果¬a,那么¬b
其逆否命题为:如果¬b,那么¬a
∧表示与,∨表示或,¬表示非
原命题与逆否命题等值。逆命题与否命题等值
原命题与逆命题以及逆否命题与否命题之间没有关系
我们继续上面的情景,如果我们要出一道题,使这道题能同时满足上面三位dalao的喜好,该如何做?
经过数学分析,满足的题目一定符合以下条件(¬a∨b∨¬c)∧(a∨b∨¬c)∧(¬a∨¬b∨c)
因此我们要做的就是给每个变量赋值,使上式值为true
是的,这就是SAT问题,但需要注意的是,上面的情况中,每个同学对题目都有三个限制,因此是3-SAT问题
可证明的,3(及以上)-SAT问题都是NPC问题(即不可使用算法解决,唯一的方法是暴力枚举)
因此,2-SAT问题是算法能解决的极限,那么我们将限制改一改:
经过一段时间的学习后,除了tqr,其他人都完全掌握了图论知识……
一波操作过后,限制条件变成了(¬a∨b)∧(a∨b)∧(¬a∨¬b),这就是我们要学习的2-SAT了
那我们就开始吧……
如何解决2-SAT?
首先,我们需要将几个互相有限制的点赋值,那就把它们丢到图里面!
建立两个点,分别是a和¬a(储存时,可以存到编号分别为 \(i\) 和 \(i+maxn\) 的节点上,就像并查集对称点一样)
那么每个点之间的关系是什么?
(a∨b)可以理解为若a为真,则b为假,反之b为真
于是我们可以建出图形:
¬a→ b∧¬b →a
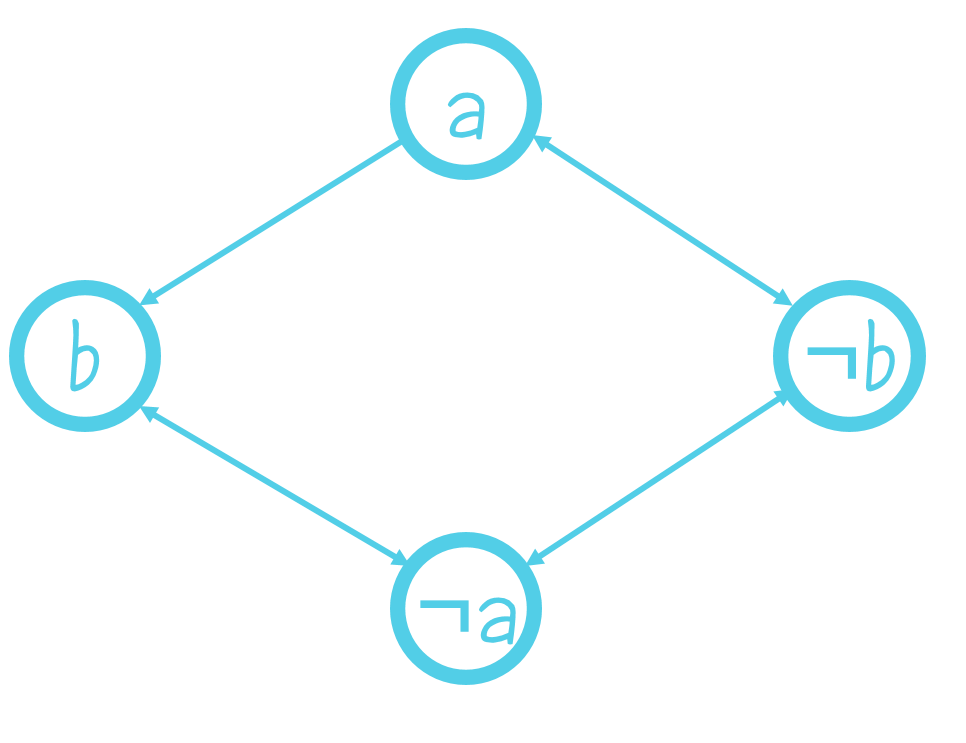
由图形可以发现,a与¬b,以及¬a与b都在同一个强连通分量里,于是我们可以得出结论:
2-SAT问题同一个强连通分量中的所有元素值相同
很显然的,如果a与¬a(或者x与¬x,x代表任意条件)在同一个强连通分量里,即他们的值相等,那么出现了矛盾,可判断问题无解(就像1=-1一样,矛盾的等式)
解决一个实际问题
题目描述
有n个布尔变量 \(x_1\)~\(x_n\),另有 \(m\) 个需要满足的条件,每个条件的形式都是 \(x_i\)为
true/false或 \(x_j\)为true/false。你的mubiao给每个变量赋值使得所有条件得到满足。输入格式
第一行两个整数\(n\)和\(m\),意义如题面所述
接下来\(m\)行每行\(4\)个整数\(i,a,j,b\),表示\(x_i\)为\(a\)或\(x_j\)为\(b\)”\((a,b∈\{0,1\})\)
输出格式
如无解,输出\(IMPOSSIBLE\);否则输出\(POSSIBLE\),
下一行\(n\)个整数\(x_1\)~\(x_n\)\((x_i∈\{0,1\})\),表示构造出的解。
很显然地,我们需要按照上述所说的来建边
read(n);read(m);
for(register int i=1;i<=m;++i)
{
read(a),read(va),read(b),read(vb);
add_edge(a+!va*n,b+vb*n);
add_edge(b+!vb*n,a+va*n);
}
然后tarjan找强连通分量(color数组是拓扑序)
void tarjan(int u)
{
low[u]=dfn[u]=++idx;
sta.push(u);
vis[u]=1;
for(register int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]) low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
for(tms++;!sta.empty();)
{
int x=sta.top();
sta.pop();
vis[x]=0;
color[x]=tms;
if(x==u) break;
}
}
}
for(register int i=1;i<=2*n;++i) if(!dfn[i]) tarjan(i);
如果强连通分量 \(x_0\), \(x_1\) 在缩点后 \(DAG\) 的底图中连通,那么我们选择的一定是拓扑序较大的
\(Tarjan\) 求强连通分量得到的强连通分量编号是遵循拓扑序逆序的,所以如果 \(x_0\) 的编号更小,输出 \(0\),否则输出 \(1\)
for(register int i=1;i<=n;++i)
if(color[i]==color[i+n])
{puts("IMPOSSIBLE");return 0;} puts("POSSIBLE");
for(register int i=1;i<=n;++i)
printf(color[i]>color[i+n]?"1 ":"0 ");
这道题就很轻松地解决了,下面是完整代码
#include<bits/stdc++.h>
using namespace std;
int n,m,a,va,b,vb;
struct Edge
{
int next,to;
}edge[2000005];
int cnt=0,head[2000005];
inline void add_edge(int from,int to)
{
edge[++cnt].next=head[from];
edge[cnt].to=to;
head[from]=cnt;
}
int low[2000005],dfn[2000005],color[2000005],tms,idx;
bool vis[2000005];
stack<int> sta;
void tarjan(int u)
{
low[u]=dfn[u]=++idx;
sta.push(u);
vis[u]=1;
for(register int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]) low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
for(tms++;!sta.empty();)
{
int x=sta.top();
sta.pop();
vis[x]=0;
color[x]=tms;
if(x==u) break;
}
}
}
template<class T>inline void read(T &res)
{
T flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
while((c=getchar())>='0'&&c<='9')res=(res<<1)+(res<<3)+c-'0';res*=flag;
}
int main()
{
read(n);read(m);
for(register int i=1;i<=m;++i)
{
read(a),read(va),read(b),read(vb);
add_edge(a+!va*n,b+vb*n);
add_edge(b+!vb*n,a+va*n);
}
for(register int i=1;i<=2*n;++i) if(!dfn[i]) tarjan(i);
for(register int i=1;i<=n;++i)
if(color[i]==color[i+n]) {puts("IMPOSSIBLE");return 0;}
puts("POSSIBLE");
for(register int i=1;i<=n;++i)
printf(color[i]>color[i+n]?"1 ":"0 ");
return 0;
}
有什么不懂的可以发qq问我,没了



