哈夫曼树的建立
哈夫曼树,又叫赫夫曼树什么其他的了,这个东西吧,主要用来对一组数据的出现概率来进行建数,这样可以使得概率大的放在前面,就使得调用简单一些,而概率小的就放到后面,其实就是对数据的一个优化处理了。
接下来我们就来看看怎么建树吧:
#include<stdio.h> #include<stdlib.h> #include<string.h> /为什么会多这么一个string呢,这是因为后面会用到一个strcpy(复制)函数 typedef struct{ int weight; int parent,lchild,rchild; }HTNode,*HuffmanTree; /哈夫曼树的结构体定义,权重,父节点,左右孩子结点 typedef char **HuffmanCode; /这个是我们的哈夫曼编码的格式转换
一:建树
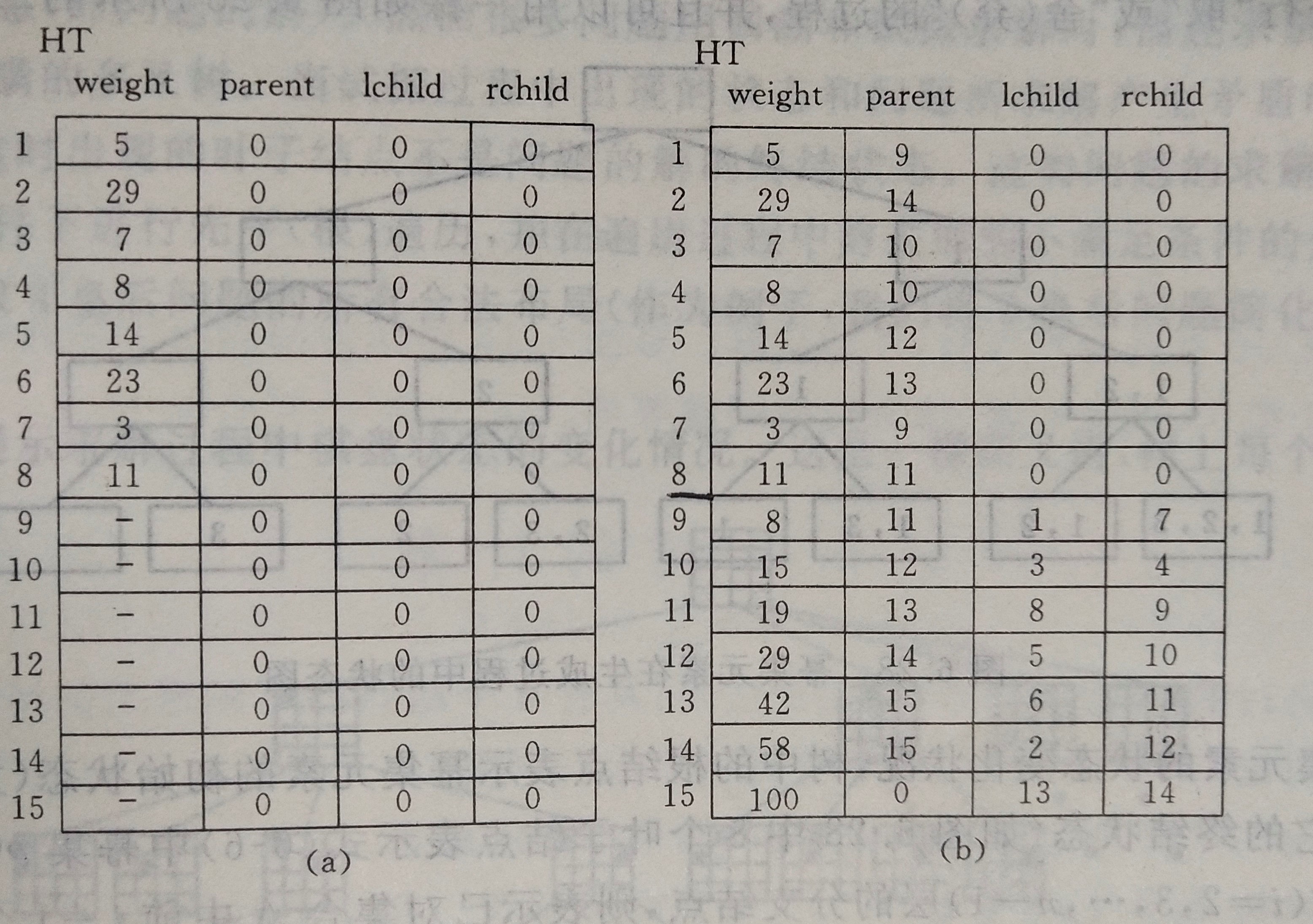
通过上表可知,首先我们对数据编号,并令其 parent ,lchild 和 rchild 初始化为 0,接下来我们通过每次选出最小的两个数据然后对其父节点进行编号,并对新生成的父节点的相关信息进行编辑,也就是它的权重,左右孩子结点,接下来继续找最小的就好了,遍历完了之后就能得到右边的这个表了,接下来就是哈夫曼编码了
看下图
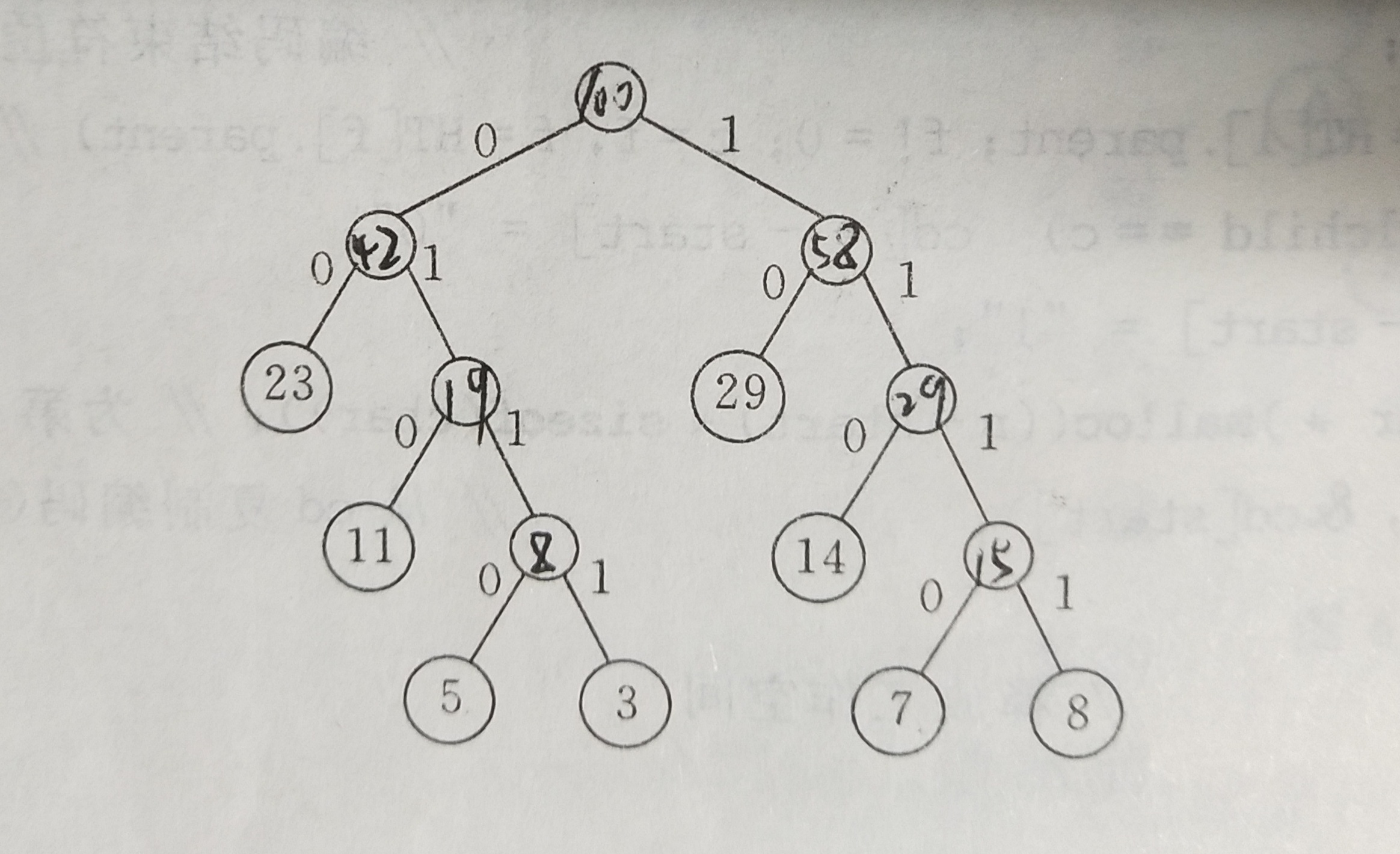
我们可以知道左边排0,右边排0,再想到我们上面的排序方式,可以知道我们需要从后面往前面进行逆向的编码,所以我们可以定义一个字符数组(也就是前面做了类型转换的),然后从尾部开始往前面赋值。
接下来就让我们看看详细的代码吧(有点小长哦):
void HuffmanCoding(HuffmanTree HT,HuffmanCode *HC,int *w,int n){ /第一个定义的就是我们哈夫曼树,第二个是字符数组,第三个就是我们的权重数组了 HuffmanTree p; int i,m,s1,s2,start,c,f; char *cd; /定义一个字符数组来进行单个数据的编码存储 if(n<=1) return; m = 2 * n -1; /m就是我们总的数据个数,包括非叶子结点 HT = (HuffmanTree)malloc((m+1) * sizeof(HTNode)); p = HT; /这里注意,要先分配空间,再进行传值,不然 p 是没有空间的 for(i = 0;i<n;i++){ /我这里写了初始的赋值函数,也可以直接在主函数里面定义 printf("请输入第 %d 个权值: ",i+1); scanf("%d",&w[i]); } for(i = 1;i<=n;++i,++w){ /这里就是把我们的初始数据进行编号 p[i].weight = *w; /因为前面我们定义的 w 是 *w 所以直接用++w就可以指向下一个数据了 p[i].parent=p[i].lchild=p[i].rchild = 0; } for( ;i<=m;++i) /然后再对后面的位置先初始化 p[i].weight=p[i].parent=p[i].lchild=p[i].rchild = 0; for(i = n+1;i<=m;++i){ /这里就开始循环找最小值了 Select(HT,i-1,&s1,&s2); /select函数用于找两个最小值,在后面哦 HT[s1].parent = i; HT[s2].parent = i; HT[i].lchild = s1; HT[i].rchild = s2; HT[i].weight = HT[s1].weight + HT[s2].weight; } printf(" weight parent lchild rchild"); for(i = 1;i<=m;i++) printf("\n%8d %8d %8d %8d",HT[i].weight,HT[i].parent,HT[i].lchild,HT[i].rchild); *HC = (HuffmanCode)malloc((n+1)*sizeof(char*)); cd = (char*)malloc(n*sizeof(char)); cd[n-1] = '\0'; for(i = 1;i<=n;++i){ start = n-1; for(c = i,f = HT[i].parent;f!=0;c = f, f = HT[f].parent) if(HT[f].lchild == c) cd[--start] = '0'; else cd[--start] = '1'; (*HC)[i] = (char*)malloc((n-start)*sizeof(char)); strcpy((*HC)[i],&cd[start]); } for(i = 1;i<=n;i++){ printf("\n %4d 的哈夫曼编码为: %s ",HT[i].weight,(*HC)[i]); } free(cd); }
二:select函数
通过上面我们知道你要写一个select函数,用来找到没有父节点的所有数据中的最小的两个,注意是没有父节点的,没有父节点代表什么,代表它还没有被找到过,因为找到过的的父节点都会被标号。
void Select(HuffmanTree HT, int k, int *s1, int *s2) { int a, b,i; *s1 = *s2 = 0; a = b = MAXVALUE; for (i = 0; i <= k; i++) { if (HT[i].parent == 0) { if (HT[i].weight < a) { b = a; a = HT[i].weight; *s2 = *s1; *s1 = i; } else if (HT[i].weight < b) { b = HT[i].weight; *s2 = i; } } } }


