算法第五章作业

算法第五章作业

最小重量机器设计问题

问题描述

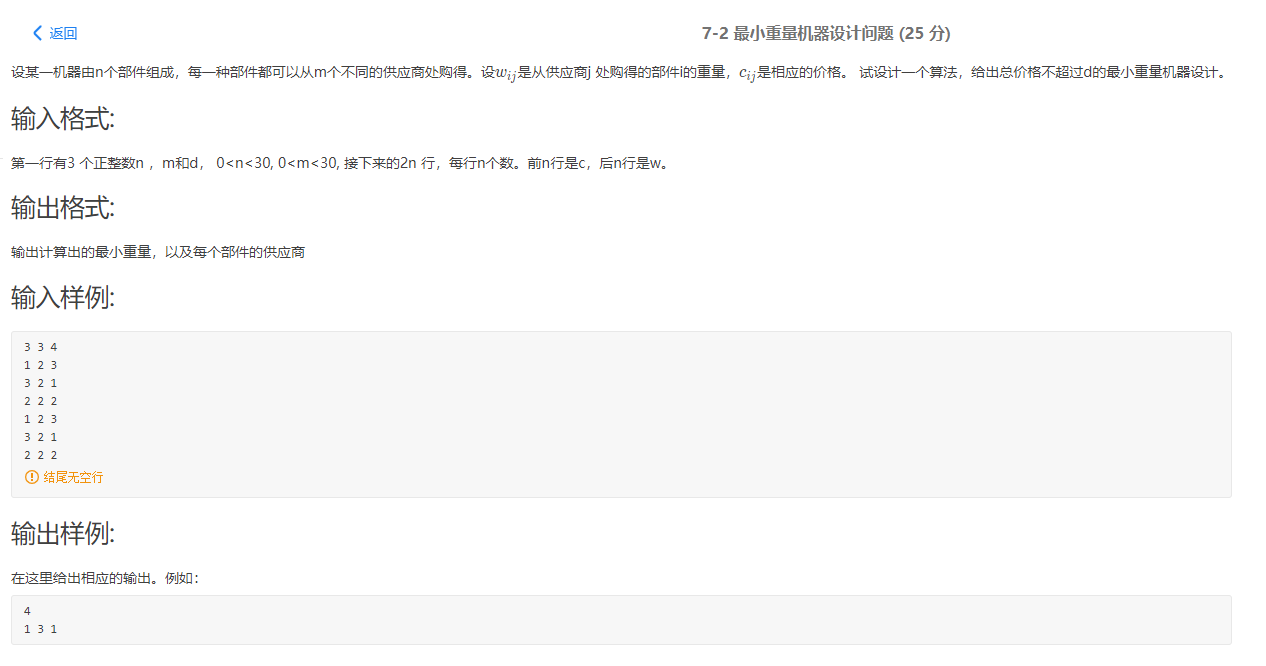
问题求解

回溯法分析

一共有n个部件，每个部件可以选择m个供应商中的一个，共有mⁿ 种方案，即有mⁿ 个解，解的集合即为解空间，解空间树为n层的m叉树。
由上至下遍历解空间树，把当前选择的商家存进x数组里，当当前价值value小于d，当前的重量小于最小的重量minweight时，继续遍历，否则进行剪枝和回溯，x数组当前的值更新为下一个商家。当向遍历到叶节点时，把最小重量minweight的值更新为当前的重量weight，把x数组记录的商家选择存进result数组里。遍历完整棵树后，minweight即为最小重量，result存储的即是商家选择的最优解。

代码

#include <iostream>
using namespace std;
int n, m, d, value, weight;
int minweight = 1000000;

int x[999];
int result[999];
int w[999][999];
int c[999][999];

void backtrack(int t){
	if(t>n){
		if(value<=d && weight<minweight){
			minweight = weight;
			for(int i=1;i<=n;i++)
				result[i] = x[i]; 
		}	
	}
	
	for(int i=1;i<=m;i++){
		x[t] = i;
		value += c[t][i];
		weight += w[t][i];
		
		if(value<=d && weight<minweight)
			backtrack(t+1);
		
		value -= c[t][i];
		weight -= w[t][i];
		
	}
}

int main(){
	cin >> n >> m >> d;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			cin >> c[i][j];
	
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			cin >> w[i][j];
			
	value = 0;
	weight = 0;
			
	backtrack(1);
	
	cout << minweight << endl;
	for(int i=1;i<=n;i++)
		cout << result[i] << ' ';  
	return 0;
}

解空间

所有总价格不超过d的每个部件的供应商选择的集合

解空间树

一颗n层的m叉树，每个分支代表选择哪个供应商

遍历解空间树的过程中，每个结点的状态值

当前的总重量weight和当前的总价格value

对回溯算法的理解

回溯算法就是个多叉树的遍历问题，主要要怎么回溯（递归）和何时回溯，为了提高效率，选用恰当的的剪枝方法和限界函数也很重要，否则算法的时间复杂度会比较高。

回溯法的基本步骤：

• 首先得构造解空间树：子集树和排列树；
• 以深度优先的方式搜索解空间：递归或迭代；
• 设计剪枝函数避免无效搜索：使用约束函数，剪去不满足约束条件的路径或使用限界函数，剪去不能得到最优解的路径。