网络流相关题目
P3376 【模板】网络最大流
题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入输出格式
输入格式:
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式:
一行,包含一个正整数,即为该网络的最大流。
输入输出样例
输入样例#1
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40
输出样例#1
50
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
const int maxN = 40007;
const int maxM = 400007;
const int inf = 0x7fffffff;
using namespace std;
int head[maxN];
int s,n,t;
int v[maxM];
int w[maxM];
int nex[maxM];
int num;
int dep[maxN];
inline int read(){
int x = 0,f = 1;char c = getchar();
while(c < '0' || c > '9') {
if(c == '-')f = -1;
c = getchar();
}
while(c >= '0' && c <= '9'){
x = x * 10 + c - '0';
c = getchar();
}
return x * f;
}
void init() {
memset(head,-1,sizeof(head));
num = -1;
return;
}
void add_Node(int U,int V,int W) {
v[++ num] = V;
nex[num] = head[U];
head[U] = num;
w[num] = W;
return ;
}
void add_(int u,int v,int w) {
add_Node(u,v,w);
add_Node(v,u,0);
return;
}
bool bfs() {
queue<int>q;
memset(dep,0,sizeof(dep));
while(!q.empty())
q.pop();
q.push(s);
dep[s] = 1;
while(!q.empty()) {
int u = q.front();q.pop();
for(int i = head[u];i != -1;i = nex[i]) {
if(w[i] > 0 && dep[v[i]] == 0) {
dep[v[i]] = dep[u] + 1;
q.push(v[i]);
}
}
}
if(dep[t])return true;
else return false;
}
int dfs(int now,int dist) {
if(now == t) return dist;
for(int i = head[now];i != -1;i = nex[i]) {
if(dep[v[i]] == dep[now] + 1 && (w[i]) != 0){
int di = dfs(v[i],min(dist,w[i]));
if(di > 0) {
w[i] -= di;
w[i ^ 1] += di;
return di;
}
}
}
return 0;
}
void Dinic() {
int Ans = 0;
while(bfs()) {
while(int d = dfs(s,inf)) {
Ans += d;
}
}
printf("%d",Ans);
return;
}
int main() {
int m;
n = read();m = read();s = read();t = read();
init();
for(int i = 1,u,v,w;i <= m;++ i) {
u = read();v = read();w = read();
add_(u,v,w);
}
Dinic();
return 0;
}
P3381 【模板】最小费用最大流
题目描述
如题,给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用。
给出两个代码,Spfa,dij+堆优化
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
const int maxN = 5000 + 7;
const int maxM = 100000 + 7 ;
using namespace std;
int n,m,s,t,ans,maxflow;
int head[maxN];
struct Node{
int u,v,flow,spend,nex;
}Map[maxM];
int dis[maxN],vis[maxN],num,path[maxN];
inline int read() {
int x = 0,f = 1;char c = getchar();
while(c < '0' || c > '9') {if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
return x * f;
}
void init() {
num = -1;
memset(head,-1,sizeof(head));
return;
}
void add_Node(int u,int v,int w,int spend) {
Map[++ num].u = u;
Map[num].spend = spend;
Map[num].flow = w;
Map[num].v = v;
Map[num].nex = head[u];
head[u] = num;
return ;
}
bool spfa() {
queue<int>q;
q.push(s);
memset(dis,0x3f,sizeof(dis));
memset(path,0,sizeof(path));
dis[s] = 0;
vis[s] = true;
while(!q.empty()) {
int p = q.front();q.pop();
vis[p] = false;
for(int i = head[p];i != -1;i = Map[i].nex) {
int v = Map[i].v;
if(dis[v] > dis[p] + Map[i].spend && Map[i].flow) {
dis[v] = dis[p] + Map[i].spend;
path[v] = i;
if(!vis[v]) {
q.push(v);
vis[v] = true;
}
}
}
}
if(dis[t] == 0x3f3f3f3f) return false;
return true;
}
int min(int a,int b) {return a > b ? b : a ;}
void f() {
int mn = 0x7fffffff;
for(int i = t;i != s;i = Map[path[i]].u)
mn = min(mn,Map[path[i]].flow);
ans += mn;
for(int i = t;i != s;i = Map[path[i]].u) {
Map[path[i]].flow -= mn;
Map[path[i] ^ 1].flow += mn;
maxflow += mn * Map[path[i]].spend;
}
}
void EK() {
while(spfa())
f();
printf("%d %d",ans,maxflow);
return ;
}
int main() {
n = read();m = read();s = read();t = read();
init();
for(int i = 1,u,v,w,f;i <= m;++ i) {
u = read();v = read();w = read();f = read();
add_Node(u,v,w,f);
add_Node(v,u,0,-f);
}
EK();
return 0;
}
// luogu-judger-enable-o2
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define re register
const int maxN = 5000 + 7;
const int maxM = 100000 + 7 ;
using namespace std;
int n,m,s,t,ans,maxflow;
int head[maxN];
struct ode{
int u,v,flow,spend,nex;
}Map[maxM];
struct Node {
int x,y;
inline bool operator < (const Node &a)const {
return y > a.y;
}
};
int dis[maxN],num,path[maxN];
priority_queue<Node>q;
inline int read() {
re int x = 0,f = 1;re char c = getchar();
while(c < '0' || c > '9') {if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
return x * f;
}
inline void init() {
num = -1;
memset(head,-1,sizeof(head));
return;
}
void add_Node(int u,int v,int w,int spend) {
Map[++ num].u = u;
Map[num].spend = spend;
Map[num].flow = w;
Map[num].v = v;
Map[num].nex = head[u];
head[u] = num;
return ;
}
bool dij() {
memset(dis,0x3f,sizeof(dis));
q.push((Node){s,0});
dis[s] = 0;
while(!q.empty()) {
Node x = q.top();q.pop();
if(x.y != dis[x.x]) continue;
for(re int i = head[x.x];i != -1;i = Map[i].nex) {
int v = Map[i].v;
if(dis[v] > dis[x.x] + Map[i].spend && Map[i].flow) {
dis[v] = dis[x.x] + Map[i].spend;
path[v] = i;
q.push((Node){v,dis[v]});
}
}
}
if(dis[t] == 0x3f3f3f3f) return false;
return true;
}
inline int min(int a,int b) {return a > b ? b : a ;}
void f() {
int mn = 0x7fffffff;
for(re int i = t;i != s;i = Map[path[i]].u)
mn = min(mn,Map[path[i]].flow);
ans += mn;
for(re int i = t;i != s;i = Map[path[i]].u) {
Map[path[i]].flow -= mn;
Map[path[i] ^ 1].flow += mn;
maxflow += mn * Map[path[i]].spend;
}
}
void EK() {
while(dij())
f();
printf("%d %d",ans,maxflow);
return ;
}
int main() {
n = read();m = read();s = read();t = read();
init();
for(re int i = 1,u,v,w,f;i <= m;++ i) {
u = read();v = read();w = read();f = read();
add_Node(u,v,w,f);
add_Node(v,u,0,-f);
}
EK();
return 0;
}
P3386 【模板】二分图匹配
二分图 感谢@一扶苏一 提供的hack数据
题目描述
给定一个二分图,结点个数分别为n,m,边数为e,求二分图最大匹配数
输入输出格式
输入格式:
第一行,n,m,e
第二至e+1行,每行两个正整数u,v,表示u,v有一条连边
输出格式:
共一行,二分图最大匹配
输入输出样例
输入样例#1: 复制
1 1 1
1 1
输出样例#1: 复制
1
说明
因为数据有坑,可能会遇到 v>mv>m 的情况。请把 v>mv>m 的数据自觉过滤掉。
算法:二分图匹配
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
const int maxN = 400007;
const int maxM = 4000007;
const int inf = 0x7fffffff;
using namespace std;
int s,t;
int head[maxN];
int v[maxM];
int w[maxM];
int nex[maxM];
int dep[maxN];
int num;
inline int read() {
int x = 0,f = 1;char c = getchar();
while(c < '0' || c > '9'){if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9'){x = x * 10 + c - '0';c = getchar();}
return x * f;
}
void init(int nn,int mm) {
s = 1;t = nn + mm + 2;
num = -1;
memset(head,-1,sizeof(head));
return;
}
void add_Node(int U,int V,int W) {
nex[++ num] = head[U];
head[U] = num;
v[num] = V;
w[num] = W;
}
void add_(int u,int v,int w) {
add_Node(u,v,w);
add_Node(v,u,0);
}
bool bfs() {
queue<int>q;
memset(dep,0,sizeof(dep));
while(!q.empty()) q.pop();
q.push(s);
dep[s] = 1;
do{
int u = q.front();q.pop();
for(int i = head[u];i != -1;i = nex[i]){
if(dep[v[i]] == 0 && w[i] > 0) {
dep[v[i]] = dep[u] + 1;
q.push(v[i]);
}
}
}while(!q.empty());
if(dep[t])return true;
return false;
}
int dfs(int now,int dist) {
if(now == t)return dist;
for(int i = head[now];i != -1;i = nex[i]) {
if(w[i] > 0 && dep[v[i]] == dep[now] + 1){
int di = dfs(v[i],min(w[i],dist));
if(di > 0) {
w[i] -= di;
w[i ^ 1] += di;
return di;
}
}
}
return 0;
}
void Dinic(){
int Ans = 0;
while(bfs()) {
while(int d = dfs(s,inf)) {
Ans += d;
}
}
printf("%d",Ans);
}
int main() {
int nn,mm,e;
scanf("%d%d%d",&nn,&mm,&e);
init(nn,mm);
for(int i = 1;i <= nn;++ i)
add_(s,i + 1,1);
for(int i = 1,u,v;i <= e;++ i) {
scanf("%d%d",&u,&v);
if(u > nn || v > mm)continue;
add_(u + 1,v + nn + 1,1);
}
for(int i = 1;i <= mm;++ i) {
add_(i + nn + 1,t,1);
}
Dinic();
return 0;
}
luogu P4013 数字梯形问题
题目描述
给定一个由 nn 行数字组成的数字梯形如下图所示。
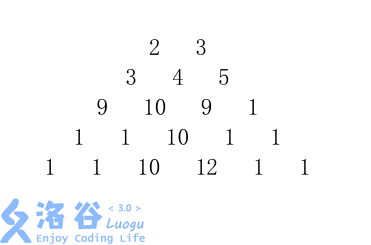
梯形的第一行有 mm 个数字。从梯形的顶部的 mm 个数字开始,在每个数字处可以沿左下或右下方向移动,形成一条从梯形的顶至底的路径。
分别遵守以下规则:
*从梯形的顶至底的 mm 条路径互不相交;
- 从梯形的顶至底的 mm 条路径仅在数字结点处相交;
*从梯形的顶至底的 mm 条路径允许在数字结点相交或边相交。
输入输出格式
输入格式:
第 11 行中有 22 个正整数 mm 和 nn ,分别表示数字梯形的第一行有 mm 个数字,共有 nn 行。接下来的 nn 行是数字梯形中各行的数字。
第 11 行有 mm 个数字,第 22 行有 m+1m+1 个数字,以此类推。
输出格式:
将按照规则 11 ,规则 22 ,和规则 33 计算出的最大数字总和并输出,每行一个最大总和。
输入输出样例
输入样例#1: 复制
2 5
2 3
3 4 5
9 10 9 1
1 1 10 1 1
1 1 10 12 1 1
输出样例#1: 复制
66
75
77
说明
$ 1 ≤m,n≤20 $
题解
- 第三个规则看起来是最简单的,感觉使用数字三角形可以做出来,不过费用流最简单,如何建图:建一个S,T,与最顶层的元素相连,费用为0,然后第i层与第i + 1层相连,费用为第i层那个元素的值.然后最后一层与T相连.费用为最后一层的元素.那么流量是多大呢,首先我们看到顶层元素只能进入一个值,所以我们S链到最顶层的流量为1.因为可以随便走,所以我们在里面流通的流量是不确定的,设为inf最为保险.最后一层也要设inf.
第二个规则仅仅在数字节点处相交,也就是不能重新过边,所以里面流通的流量设为1就好.- 有个细节要注意(考试中差点入坑).最后一层连到T节点时一定要注意流量为inf,我们的T是一个虚点,连到最后一层的时候,已经是完成了,因为最后一层的一个点,有两个地方转移.
- 第一个规则拆点,就是将一个点拆成两个,流量为1,费用为0,为什么要拆点呢,因为我们不知道这个点走没走过,如果用vis的话,退流的操作很玄学我们不知道什么时候退流,所以我们可以用拆点的形式.顺带一提,最后一层不用拆点,直接将流量设为1就好.(T就是一个虚点)
// luogu-judger-enable-o2
#include <bits/stdc++.h>
#include <queue>
const int MAXN = 50000 + 7;
const int maxn=0x3f3f3f3f;
using namespace std;
struct node {
int u,v,flow,spend,nxt;
}edge[MAXN];
int head[MAXN];
int num,maxsize;
int n,m,s,t;
int ans,maxflow;
int dis[MAXN];
int vis[MAXN];
int from[MAXN];
int fx[407][407];
int id[407][407];
int id2[407][407];
inline int read() {
int x = 0,f = 1;char c = getchar();
while(c < '0' || c > '9') {if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
return x * f;
}
void add_edge(int x,int y,int z,int c)
{
edge[num].u=x;
edge[num].v=y;
edge[num].flow=z;
edge[num].spend=c;
edge[num].nxt=head[x];
head[x]=num++;
}
void add(int x,int y,int z,int c) {
add_edge(x,y,z,c);
add_edge(y,x,0,-c);
}
bool SPFA()
{
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s] = 0;
queue<int> q;
q.push(s);
vis[s] = 1;
while(!q.empty())
{
int p = q.front();
q.pop();
vis[p] = 0;
for(int i = head[p];i != -1;i = edge[i].nxt)
{
if(dis[edge[i].v] > dis[edge[i].u] + edge[i].spend && edge[i].flow > 0)
{
dis[edge[i].v] = dis[edge[i].u] + edge[i].spend;
from[edge[i].v] = i;
if(!vis[edge[i].v])
{
vis[edge[i].v] = 1;
q.push(edge[i].v);
}
}
}
}
if(dis[t] != maxn)
return 1;
else
return 0;
}
void f()
{
int mn = maxn;
for(int i = t;i != s;i = edge[from[i]].u)
mn = min(mn,edge[from[i]].flow);
for(int i = t;i != s;i = edge[from[i]].u)
{
edge[from[i]].flow -= mn;
edge[from[i] ^ 1].flow += mn;
ans += (mn * edge[from[i]].spend);
}
maxflow += mn;
}
void init() {
memset(head,-1,sizeof(head));
num = 0;
maxsize = 0;
ans = 0;
maxflow = 0;
return;
}
void Dinic() {
while(SPFA()) {
f();
}
printf("%d\n",- ans);
}
void work2() {
init();
for(int i = 1;i <= m;++ i) {
for(int j = 1;j <= n + i - 1;++ j) {
maxsize ++;
id[i][j] = maxsize;
}
}
s = ++ maxsize;t = ++ maxsize;
for(int i = 1;i <= m;++ i) {
for(int j = 1;j <= n + i - 1;++ j) {
add(id[i][j],id[i + 1][j],1,- fx[i][j]);
add(id[i][j],id[i + 1][j + 1],1,- fx[i][j]);
}
}
for(int i = 1;i <= n;++ i)
add(s,id[1][i],1,0);
for(int i = 1;i <= m + n - 1;++ i)
add(id[m][i],t,maxn,- fx[m][i]);
Dinic();
}
void work3() {
init();
for(int i = 1;i <= m;++ i) {
for(int j = 1;j <= n + i - 1;++ j) {
maxsize ++;
id[i][j] = maxsize;
maxsize ++;
id2[i][j] = maxsize;
}
}
s = ++ maxsize;t = ++ maxsize;
for(int i = 1;i <= m;++ i) {
for(int j = 1;j <= n + i - 1;++ j) {
add(id[i][j],id2[i][j],1,0);
add(id2[i][j],id[i + 1][j + 1],1,- fx[i][j]);
add(id2[i][j],id[i + 1][j],1,- fx[i][j]);
}
}
for(int i = 1;i <= n;++ i)
add(s,id[1][i],1,0);
for(int i = 1;i <= m + n - 1;++ i) {
add(id[m][i],t,1,- fx[m][i]);
//add(id2[m][i],t,maxn,0);
}
Dinic();
}
void work1() {
init();
for(int i = 1;i <= m;++ i) {
for(int j = 1;j <= n + i - 1;++ j) {
maxsize ++;
id[i][j] = maxsize;
}
}
s = ++ maxsize;t = ++ maxsize;
for(int i = 1;i <= m;++ i) {
for(int j = 1;j <= n + i - 1;++ j) {
add(id[i][j],id[i + 1][j],maxn,- fx[i][j]);
add(id[i][j],id[i + 1][j + 1],maxn,- fx[i][j]);
}
}
for(int i = 1;i <= n;++ i)
add(s,id[1][i],1,0);
for(int i = 1;i <= m + n - 1;++ i)
add(id[m][i],t,maxn,- fx[m][i]);
Dinic();
}
int main(){
n = read();m = read();
for(int i = 1;i <= m;++ i)
for(int j = 1;j <= n + i - 1;++ j)
fx[i][j] = read();
work3();
work2();
work1();
return 0;
}
题目链接: luogu P2756
luogu P2756 飞行员配对方案问题
题目背景
第二次世界大战时期..
题目描述
英国皇家空军从沦陷国征募了大量外籍飞行员。由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的2 名飞行员,其中1 名是英国飞行员,另1名是外籍飞行员。在众多的飞行员中,每一名外籍飞行员都可以与其他若干名英国飞行员很好地配合。如何选择配对飞行的飞行员才能使一次派出最多的飞机。对于给定的外籍飞行员与英国飞行员的配合情况,试设计一个算法找出最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
对于给定的外籍飞行员与英国飞行员的配合情况,编程找出一个最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
输入输出格式
输入格式:
第 1 行有 2 个正整数 m 和 n。n 是皇家空军的飞行员总数(n<100);m 是外籍飞行员数(m<=n)。外籍飞行员编号为 1~m;英国飞行员编号为 m+1~n。
接下来每行有 2 个正整数 i 和 j,表示外籍飞行员 i 可以和英国飞行员 j 配合。最后以 2个-1 结束。
输出格式:
第 1 行是最佳飞行员配对方案一次能派出的最多的飞机数 M。接下来 M 行是最佳飞行员配对方案。每行有 2个正整数 i 和 j,表示在最佳飞行员配对方案中,飞行员 i 和飞行员 j 配对。如果所求的最佳飞行员配对方案不存在,则输出‘No Solution!’。
输入输出样例
输入样例#1 :
5 10
1 7
1 8
2 6
2 9
2 10
3 7
3 8
4 7
4 8
5 10
-1 -1
输出样例#1:
4
1 7
2 9
3 8
5 10
思路:模板二分图匹配,但是会发现,要输出方案,我们只需要判断,两个飞行员之间的流量是否为0就OK了,注意这里不能使用vis[i][j]表示i到j个飞行员是否可行,因为有退流操作.
下面是vis[i][j]判断是否可行的代码,WA 63.
#include "iostream"
#include "cstdio"
#include "queue"
#include "algorithm"
#include "cstring"
const int maxN = 1e2 + 7;
const int maxM = 1e4 + 5;
const int inf = 0x7fffffff;
using namespace std;
int n,m,s,t;
int head[maxN];
int nex[maxM];
int v[maxM];
int w[maxM];
int dep[maxN];
int num;
bool vis[maxN][maxN];
void init() {
s = 1;t = n + 2;
num = -1;
memset(head,-1,sizeof(head));
return;
}
inline int read() {
int x = 0,f = 1;char c = getchar();
while(c < '0' || c > '9') {if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
return x * f;
}
void add_Node(int U,int V,int W) {
v[++num] = V;
w[num] = W;
nex[num] = head[U];
head[U] = num;
}
void add(int u,int v,int w) {
add_Node(u,v,w);
add_Node(v,u,0);
}
bool bfs() {
memset(dep,0,sizeof(dep));
queue<int>q;
while(!q.empty())
q.pop();
q.push(s);
dep[s] = 1;
do{
int p = q.front();q.pop();
for(int i = head[p];i != -1;i = nex[i]) {
if(w[i] && dep[v[i]] == 0) {
q.push(v[i]);
dep[v[i]] = dep[p] + 1;
}
}
}while(!q.empty());
if(dep[t]) return true;
return false;
}
int dfs(int now,int dist) {
if(now == t) return dist;
for(int i = head[now];i != -1;i = nex[i]) {
if(dep[v[i]] == dep[now] + 1 && w[i] && vis[now][v[i]] == false) {
int di = dfs(v[i],min(dist,w[i]));
if(di) {
w[i] -= di;
w[i ^ 1] += di;
vis[now][v[i]] = true;
return di;
}
}
}
return 0;
}
void Dinic() {
int Ans = 0;
while(bfs()) {
while(int d = dfs(s,inf)) {
Ans += d;
}
}
printf("%d\n",Ans);
for(int i = 2;i <= m + 1;++ i) {
for(int j = m + 2;j <= n + 1;++ j) {
if(vis[i][j]) {
printf("%d %d\n",i - 1,j - 1);
break;
}
}
}
return;
}
int main() {
scanf("%d%d",&m,&n);
init();
for(int i = 2;i <= m + 1;++ i)
add(s,i,1);
for(int i = m + 2;i <= n + 1;++ i)
add(i,t,1);
int u,v;
while(scanf("%d%d",&u,&v) && u != -1)
add(u + 1,v + 1,1);
Dinic();
return 0;
}
下面是AC代码
#include "iostream"
#include "cstdio"
#include "queue"
#include "algorithm"
#include "cstring"
const int maxN = 1e2 + 7;
const int maxM = 1e4 + 5;
const int inf = 0x7fffffff;
using namespace std;
int n,m,s,t;
int head[maxN];
int nex[maxM];
int v[maxM];
int w[maxM];
int dep[maxN];
int num;
bool vis[maxN][maxN];
void init() {
s = 1;t = n + 2;
num = -1;
memset(head,-1,sizeof(head));
return;
}
inline int read() {
int x = 0,f = 1;char c = getchar();
while(c < '0' || c > '9') {if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
return x * f;
}
void add_Node(int U,int V,int W) {
v[++num] = V;
w[num] = W;
nex[num] = head[U];
head[U] = num;
}
void add(int u,int v,int w) {
add_Node(u,v,w);
add_Node(v,u,0);
}
bool bfs() {
memset(dep,0,sizeof(dep));
queue<int>q;
while(!q.empty())
q.pop();
q.push(s);
dep[s] = 1;
do{
int p = q.front();q.pop();
for(int i = head[p];i != -1;i = nex[i]) {
if(w[i] && dep[v[i]] == 0) {
q.push(v[i]);
dep[v[i]] = dep[p] + 1;
}
}
}while(!q.empty());
if(dep[t]) return true;
return false;
}
int dfs(int now,int dist) {
if(now == t) return dist;
for(int i = head[now];i != -1;i = nex[i]) {
if(dep[v[i]] == dep[now] + 1 && w[i] && vis[now][v[i]] == false) {
int di = dfs(v[i],min(dist,w[i]));
if(di) {
w[i] -= di;
w[i ^ 1] += di;
vis[now][v[i]] = true;
return di;
}
}
}
return 0;
}
void Dinic() {
int Ans = 0;
while(bfs()) {
while(int d = dfs(s,inf)) {
Ans += d;
}
}
printf("%d\n",Ans);
for(int i = 2;i <= m + 1; ++ i ) {
for(int j = head[i];j != -1;j = nex[j]) {
if( w[j] == 0 && v[j] > m + 1) {
printf("%d %d\n",i - 1,v[j] - 1);
break;
}
}
}
return;
}
int main() {
scanf("%d%d",&m,&n);
init();
for(int i = 2;i <= m + 1;++ i)
add(s,i,1);
for(int i = m + 2;i <= n + 1;++ i)
add(i,t,1);
int u,v;
while(scanf("%d%d",&u,&v) && u != -1)
add(u + 1,v + 1,1);
Dinic();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号