主席树学习笔记
主席树(一个简单的数据结构花了我一天的时间整理)
主席树可以用来解决如下问题：“给出一列数,a1,a2…an,每次询问其中连续的一段区间ai到aj其中的第K小的数是多少？”(询问次数为5000,序列长度≤2e5)
我们应如何做呢.
每次询问排序??显然复杂度是巨大的
那么接下来我们要学习主席树(一个可持续化数据结构)
可持续化:能够查询历史版本.
何谓查询历史版本: 例如我们执行一些操作:
你还剩下1,1,1,2,2这些牌.假设你打出了对二(当然,现实生活中是不会有人这样出的)然后你发现你手里有三张一样的牌,然后你想撤销以前的操作,然后你就回到刚开始的时候.这在我们编程里怎样体现呢.就是存起以前的状态.然后进行一些撤销操作之类的.这就是查询历史版本.
想要学会主席树.我们还要学会
- 权值线段树 :
前缀和.
权值线段树
来了解一下权值线段树吧.
与线段树相差无几,唯一的不同之处就是他的(数组)下标为x的数组所存的值是数组中有当前值的数的个数
例如我们有这么一些数: 1.2.3.4.4.3.2.1
假设我们要 求出5 ~ 8这个区间的第三大数.
我们就会构造这么两个图
现在我们来模拟一下如何用权值线段树查询[5,8]第三大数.
首先我们对比一下根节点的左孩子的个数,我们会发现4 - 2 = 2 ,2 < 3,所以相比以前的版本多出了两个元素,因为我们要找第三大.所以我们去右孩子去找第k大元素,直到根节点为止.
这就是前缀和的思想.但是我们要找这么多区间.每一次都要造一个[1,i] (i不确定)的区间.然后去查询,显然空间复杂度是巨大的.
接下来我们要开始正式学习主席树啦.
空间巨大怎么办,显然我们可以利用他们的一些共同信息.
当新加入一个点的时候,只有一条链上发生改变.
我们有这样一个序列.
长度为7,询问数为1.
1 5 2 6 3 7 4
2 5 3
ps先离散化,存的是数组下标.
然后我们建立这样一颗空树(线段树)
ps连线画歪了,注意qwq.
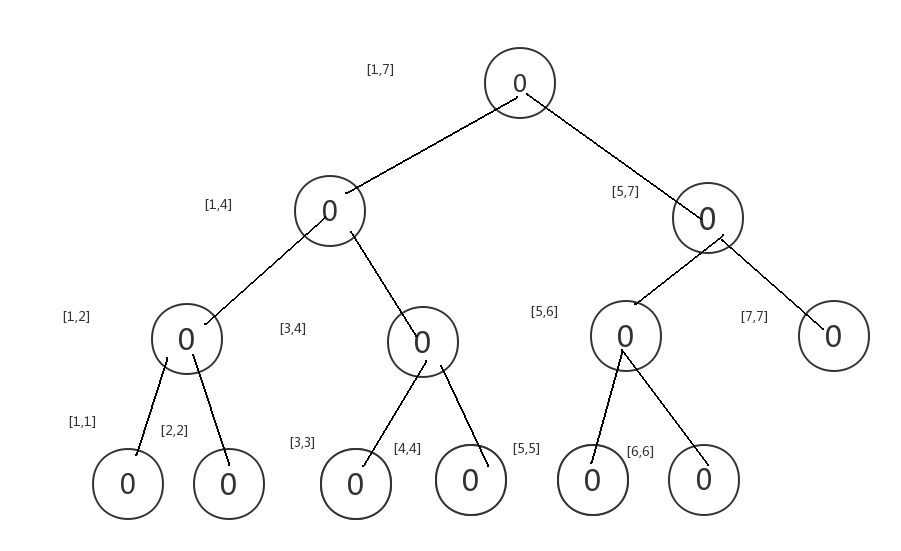
当然,点值都为0.
我们插入1.
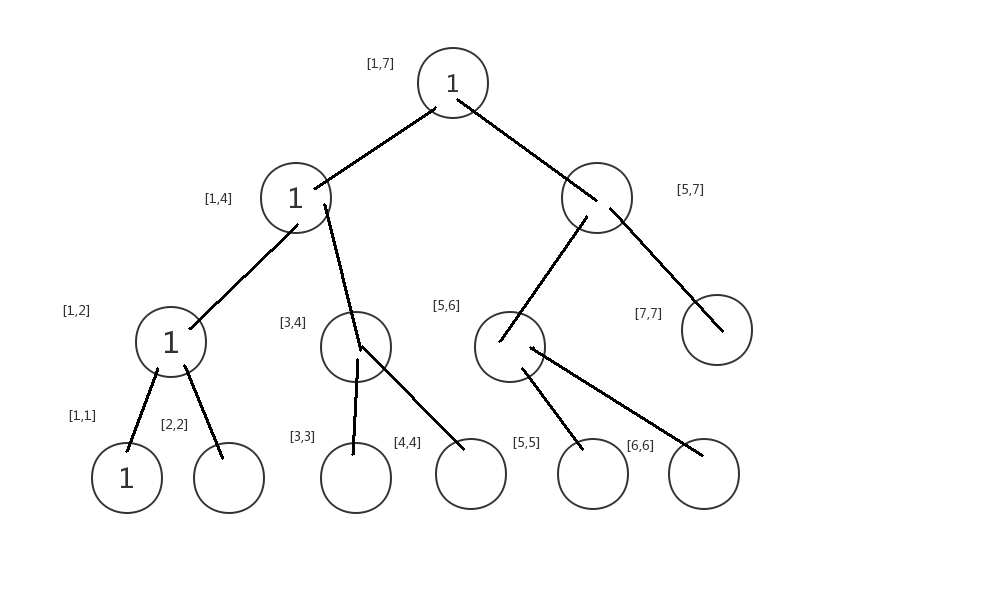
然后这样插入插入.形成了这颗树(没有连边,注意.)
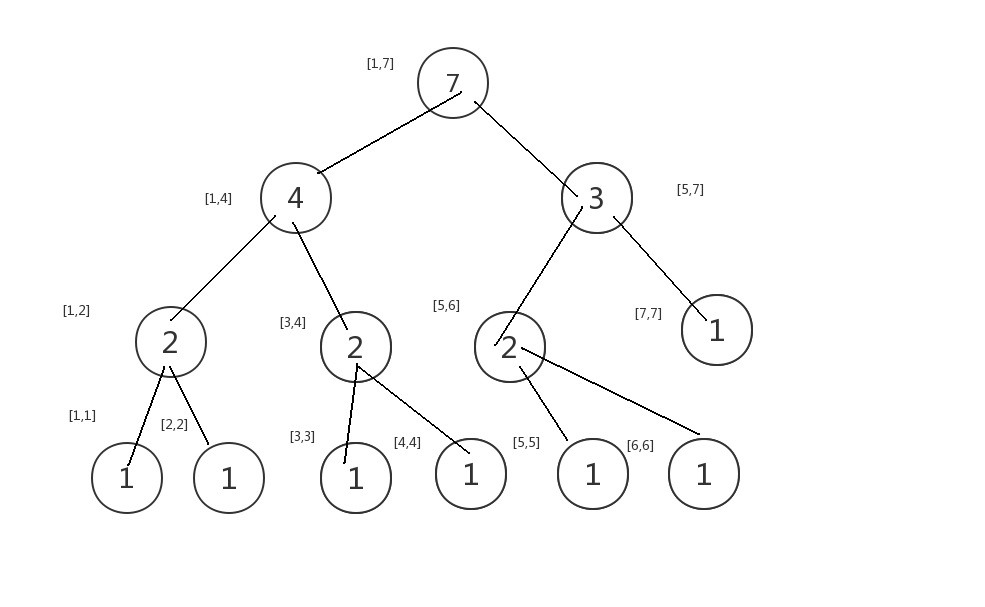
然后我们拿出l - 1颗树和第r颗树也就是1和5这颗.
利用我们刚才的权值线段树所学的知识相减即可.
但我们还没有步入正题.如何共用一些公共节点.
假设我们构造好了[1,4]这个区间,然后we need add a num.
还是以上面的例子.
构造好了的[1,4]区间是这个样子的.
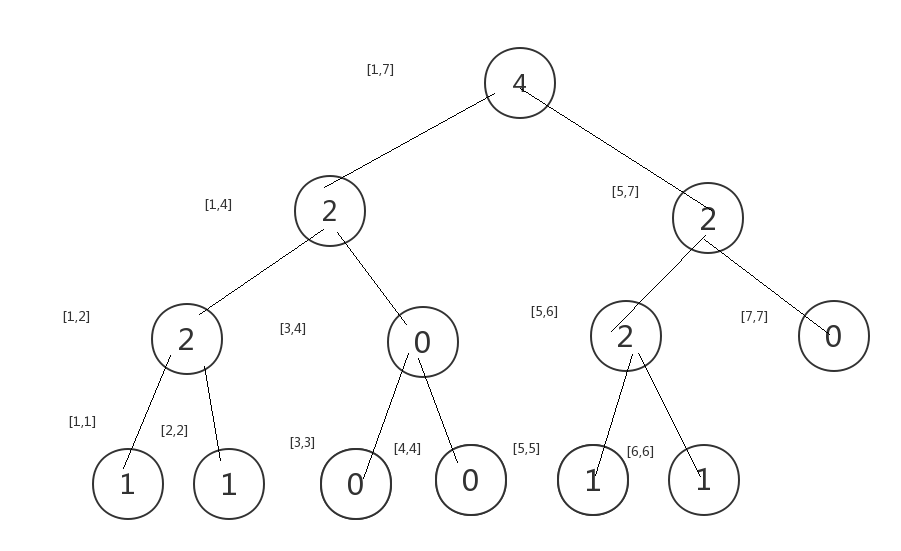
此时我们添加第5个元素,也就是3.
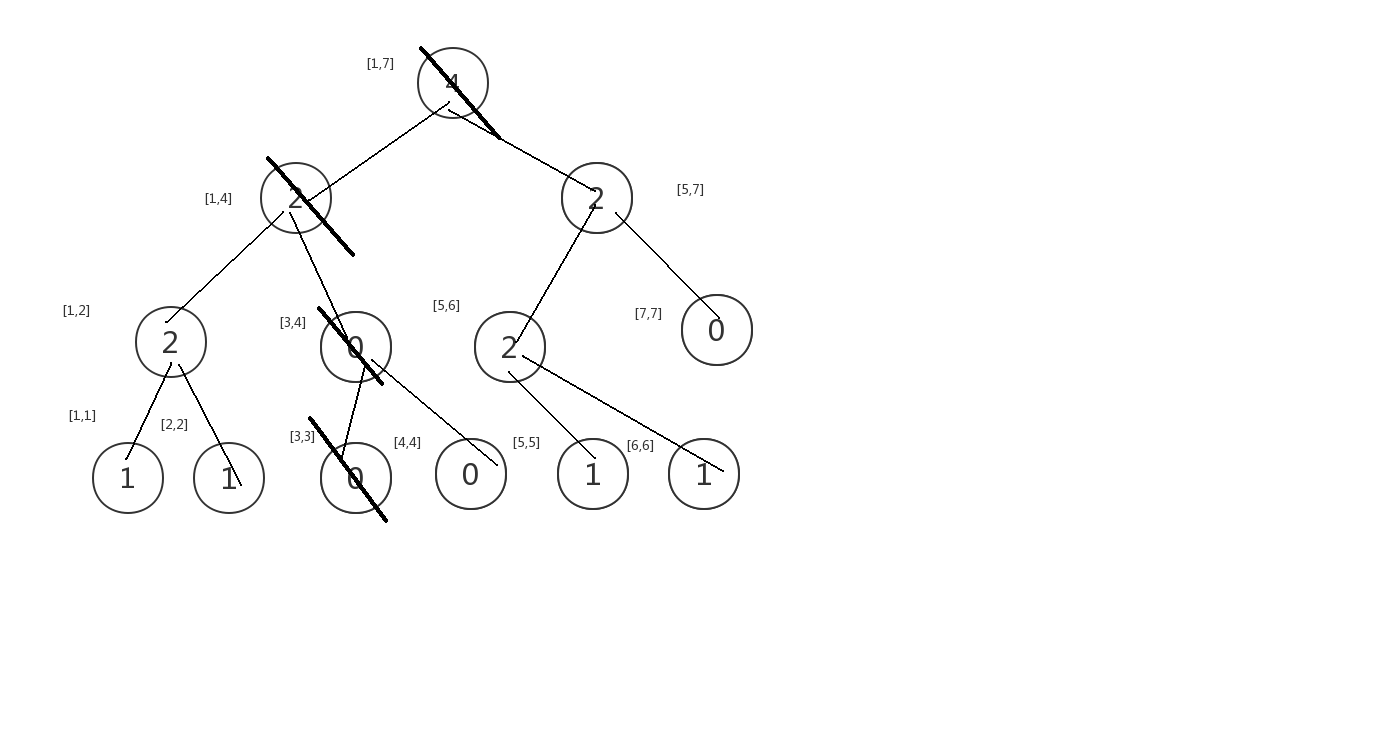
这条路径是我们要修改的路径.
当我们修改一个树的左子树时,它的右子树是不变的,我们可以借用它.
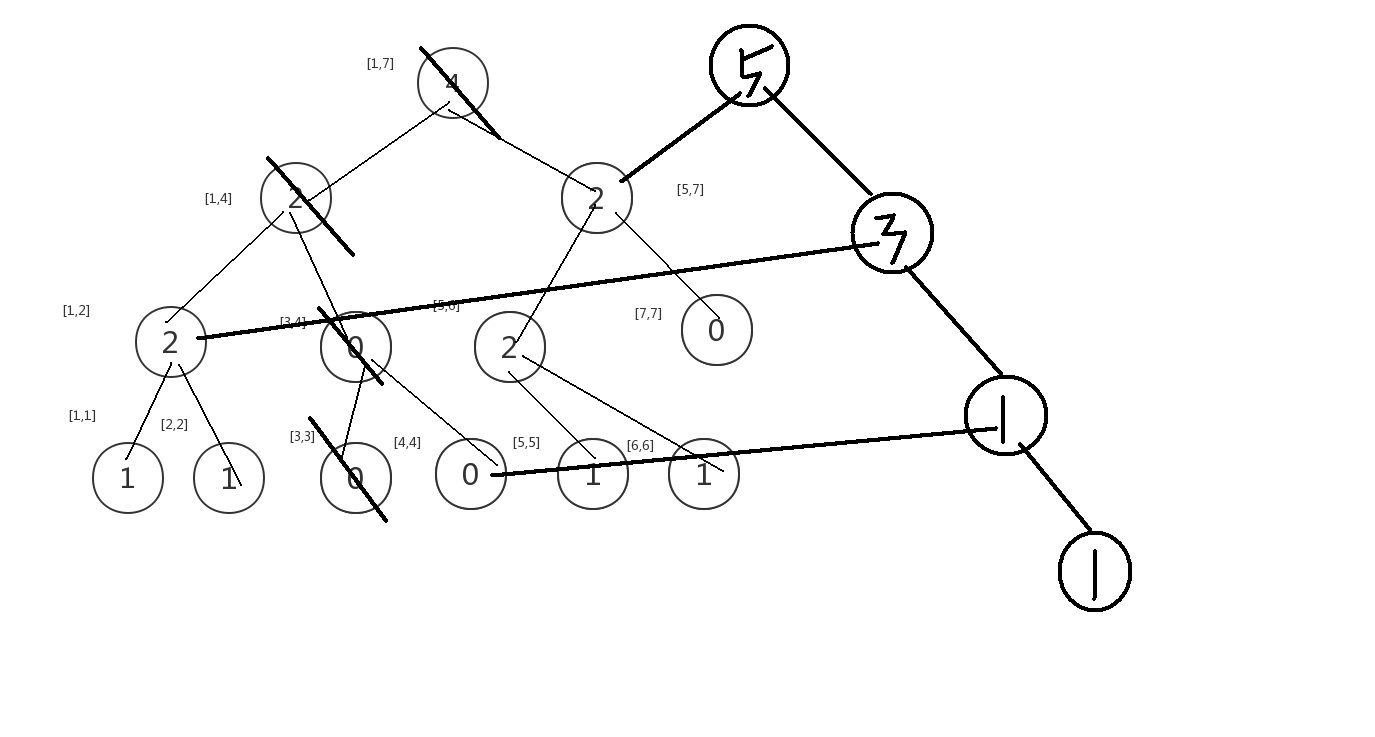
当我们更新到next点的时候,我们就会利用上图的这个.以前的那个就成了历史版本了.
准备一天的主席树终于敲完了
luogu P3834 【模板】可持久化线段树 1（主席树
code
#include <iostream>
#include <algorithm>
#include <cstdio>
const int maxN = 2e5 + 7;
using namespace std;
int root[maxN],cnt,s[maxN],a[maxN];
struct Node {int lc,rc,w;}tree[maxN * 20];
inline int read() {
int x = 0,f = 1;char c = getchar();
while(c < '0' || c > '9') {if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
return x * f;
}
void add(int &now,int last,int l,int r,int x) {
now = ++cnt;
tree[now].w = tree[last].w + 1;
tree[now].lc = tree[last].lc;tree[now].rc = tree[last].rc;
if(l == r)return;
int mid = (l + r) >> 1;
if(x <= mid) add(tree[now].lc,tree[last].lc,l,mid,x);
else add(tree[now].rc,tree[last].rc,mid + 1,r,x);
return;
}
int query(int L,int R,int l,int r,int x) {
if(l == r)return l;
int mid = (l + r) >> 1;
int p = tree[tree[R].lc].w - tree[tree[L].lc].w;
if(p < x) return query(tree[L].rc,tree[R].rc,mid + 1,r,x - p);
else return query(tree[L].lc,tree[R].lc,l,mid,x);
}
int main() {
int n,m;
n = read();m = read();
for(int i = 1;i <= n;++ i) {s[i] = a[i] = read();}
sort(s + 1,s + n + 1);
for(int i = 1;i <= n;++ i ){
int p = lower_bound(s + 1,s + n + 1,a[i]) - s;
add(root[i],root[i - 1],1,n,p);}
int l,r,x;
while(m -- ) {
l = read();r = read();x = read();
int y = query(root[l - 1],root[r],1,n,x);
printf("%d\n",s[y]);
}
return 0;
}
qwq.有不理解或者本文有错误的.欢迎骚扰.QQnum:3361879051.
