经典排序方法及细节小结(2)

紧接上篇的插入排序  交换排序算法的分析小结，这一篇小结经典排序算法中另外几个算法

选择排序

假使对一个n个大小的序列排序

（1）直接选择排序

思路：

①遍历一遍数组，选择一个最大(小)的值将其放到最后的位置

②在剩下的N-1个元素中，再选一个最大(小)的放到后面（倒数第二位置）

③不断重复以上操作，当只剩下一个元素时结束算法

优化：

操作①时 可以找到最大值和最小值，将最大值放到最后的同时还可以把最小值放到最前面，这样的话一趟排序就能确定两个元素的位置了，一定程度上提高了效率。

优化中注意：如果最大元素本来就是数组首元素即a[left]，当最小数和a[left]交换位置后最大元素的位置已经改变了，这就会导致排序错误。

注意了以上问题就容易写出代码：

void SelectSort(int* arr, size_t length)
{
    assert(arr && length > 0);

    int left = 0;
    int right = length - 1;
    
    while(left < right)
    {
        int min = left;
        int max = left;
        for(int i = left; i <= right; ++i)
        {
            if(arr[i] < arr[min])
                min = i;
            if(arr[i] > arr[max])
                max = i;
        }
        Swap(&arr[left], &arr[min]);
        if(left == max)       //max 对应a[left] 
            max = min;
        Swap(&arr[right], &arr[max]);
        left++; right--;
       // Print(arr, length);
    }
}

 

时间复杂度：最好：O(N*N)    最坏：O(N*N)    平均：O(N*N)

空间复杂度：O(1)

稳定性：不稳定

 

（2）堆排序

堆排序以其不错排序效率，以及O(1)的空间复杂度成为实际应用中最为广泛的一种排序。

实现排序之前，先介绍一个建堆和实现堆排都会用到的调整算法：向下调整算法

它的作用就是将要调整元素向下调整至一个合适的位置，使该元素子树结点都比它小，父辈结点都比它大。

typedef int DataType;

void AdjustDownToBigHeap(DataType* arr, size_t n, size_t curRoot)
{
    assert(arr);

    size_t parent = curRoot;
    size_t child = (parent<<1) + 1;
    while(child < n)
    {
        if(arr[child] < arr[child+ 1] && child+1 < n)  //找到更大的子结点
            ++child;
        if(arr[child] > arr[parent])        //子结点比父结点大，就交换
            Swap(&arr[child], &arr[parent]);
        //继续往下调整
        parent = child;            
        child = (parent<<1)+ 1;
    }
}

 

堆排实现思路：

①首先将数组按排序码大小建堆，若排升序，建大堆(建大堆很关键)；（这里假设排升序；若是排降序，就建小堆）

②begin指向堆顶，end指向堆尾，堆顶堆尾元素相交换 (此时堆顶就是排序码最大的元素了)，堆尾元素前移(--end)，堆的范围少1。

③再将堆顶元素向下调整，在新范围内让堆继续保持大堆的样式

④重复②③，直到end = 0 结束(n−2)>>1

如对序列{10,20,3,12,16,18,25 ,17,14,19}  建好大堆以后，交换堆头堆尾的值，然后向下调整过程如下：

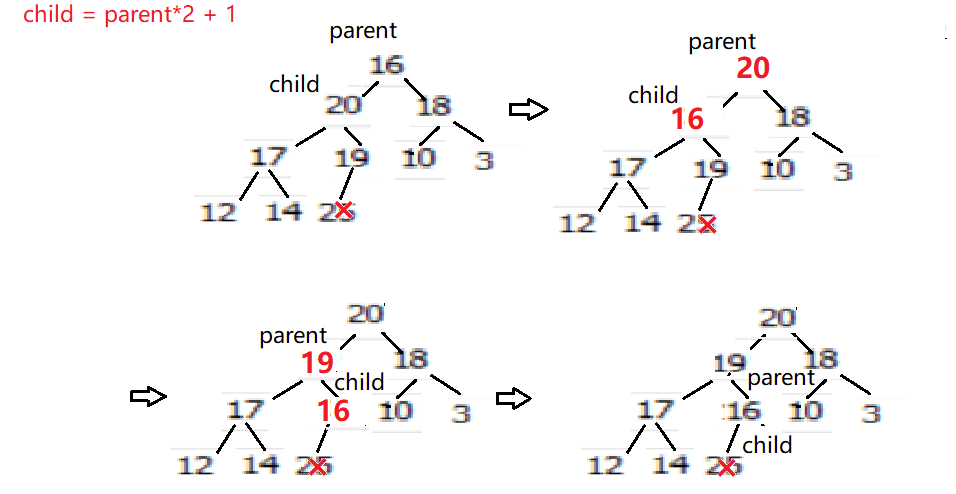
注意：

排升序是不能建小堆的，因为小堆一次只能确定出来最小的那个元素值，虽然小堆中每一个节点的子树的结点都比根结点的值小，但是无法确定左右子结点的谁更小一点，这样排序过程中就无法确定次最小的元素，要排序的话就得重新建堆了，十分拉低效率的。

堆排代码：

void HeapSort(DataType* arr, int n)
{
    assert(arr);
    //建一个大堆
    int i = (n -1)>>1;
    for(; i >= 0; --i)
    {
        AdjustDownToBigHeap(arr, n, i);  //向下调整算法
    }
    //堆头堆尾交换位置，将堆头位置处的值向下调整
    int end = n - 1;
    while(end > 0)
    {
        Swap(&arr[0], &arr[end]);
        AdjustDownToBigHeap(arr, end, 0);
        --end;
    }
}

时间复杂度：最好：O(NlogN)    最坏：O(NlogN)  平均：O(NlogN)

空间复杂度：O(1)

稳定性：不稳定

 

归并排序

归并排序

归并排序和快排思路基本相同，只不过归并排序额外开辟了O(N)的空间来帮助排序，使得在它最坏的情况也能保持O(NlogN)的时间复杂度，所以相对来说，它是一种更加优良的排序算法，只是耗费了更多的空间。

思路：

①当二分为只剩下两个或一个元素的时候，比较大小排序。

②递归回溯时，借助开辟的空间将数组两两进行合并，并且合并后保持有序。

③回溯完毕后，整个数组就有序了 。

注意：

在利用开辟的空间进行合并，其合并的方法与两条有序链表的合并差不多，只是它不能像链表那样直接进行结点的连接；这里是是按排序码大小依次将放进开辟的数组里面，这样数组里面存放的序列就是有序的了，然后再将这段序列拷贝回原来位置。

代码：

void MergeArr(int* arr, int left, int mid, int right)
{
    int* tmp = (int*)malloc(sizeof(int) * (right -left +1)); //开辟一个中间数组
    int begin1 = left, end1 = mid;
    int begin2 = mid + 1, end2 = right;
    int index = 0;
    
    //归并在一起
    while(begin1 <= end1 && begin2 <= end2)
    {
        if(arr[begin1] <= arr[begin2])
            tmp[index++] = arr[begin1++];
        else
            tmp[index++] = arr[begin2++];
    }
    //如果分成两个数组中一边还有剩余,烤过去
    while(begin1 <= end1)
        tmp[index++] = arr[begin1++];
    while(begin2 <= end2)
        tmp[index++] = arr[begin2++];
    
    //将tmp保存好的有序数据再拷回原数组
    for(int i = left; i<= right; ++i)
        arr[i] = tmp[i-left];

    free(tmp);
}
void MergeSort(int* arr, int left, int right)
{
    assert(arr);
    if(left >= right)
        return;
    int mid = left + ((right - left)>> 1);
    MergeSort(arr, left, mid);
    MergeSort(arr, mid+ 1, right);
    MergeArr(arr, left, mid, right);
}

 

时间复杂度：最好：O(NlogN)    最坏：O(NlogN)    平均：O(NlogN)

空间复杂度：O(N)

对应两个相同排序码的元素，在排序合并时，在前面的就会先进行合并，合并后并不会影响它们的相对位置

稳定性：稳定

 

 计数排序

计数排序

基本思路就是对于给定的输入序列中的每一个元素x，统计该序列中值为x的元素的个数 。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。它的原理跟哈希表的K-V模型类似。

思路：
①遍历一遍数组，得出数组的范围range，创建一个大小为range的数组，即哈希表，初始化为全0。
②再从头开始遍历数组，数字重复出现一次，在其相应的位置对应的数值加1。
③从左到右开始遍历哈希表，将数值不为0的位置的下标存储到原数组中，且数值是多少就存储多少个 。

注意：

①此种排序是依靠一个辅助数组来实现，不基于比较，遍历常数遍数组即可，所以时间复杂度较低；但由于要一个辅助数组C，所以空间复杂度要大一些，由于计算机的内存有限，所以这种算法适合排范围小、值密集的序列，不适合范围很大的序列。

②给哈希表分配空间大小时，考虑这样一个问题：例如我有10000个数，范围在10001~20000之间，此时就直接开辟20000的空间大小？很明显这样搞是很浪费的。对此，我们何不先遍历一遍数据，找出最大值与最小值，求出数据范围 (然后用1代表10001,10000代表20000)，这样我们就仅需开辟10000个空间即可 节约了大量空间。

    

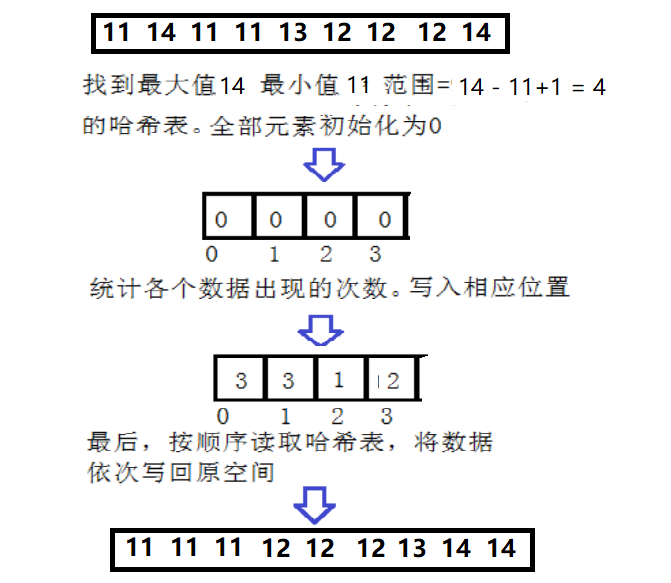
时间复杂度：不难看出我们总需要三趟遍历，前两趟统计数据出现次数，遍历原数据、确定辅助数组范围，复杂度为O(N)；最后一趟遍历哈希表，向原空间写数据,遍历了range范围次，所以总的时间复杂度为O(N+range)。

空间复杂度：开辟了范围（range）大小的辅助哈希表，所以空间复杂度为O(range)。

稳定性：可稳定

代码：

void CountSort(int* arr, int length)  
{  
    assert(arr && length > 0);  

    int max = arr[0];  
    int min = arr[0];  
    //选出最大数与最小数，确定哈希表的大小  
    for (int i = 0; i < length; ++i)  
    {  
        if (arr[i] > max)   
            max = arr[i];  
        if (arr[i] < min)  
            min = arr[i];   
    }  
    int range = max - min + 1;  

    int *pCount = (int*)malloc(sizeof(int) * range);  
    memset(pCount, 0, sizeof(int)*range);  //将开辟空间初始化成0  

    //确定相同元素的个数
    for (int i = 0; i < length; ++i)  
        pCount[arr[i] - min]++;   
    
    //将数据重新写回数组  
    int j = 0;  
    for (int i = 0; i < range; ++i)  
    {  
        while (pCount[i]-- > 0)  //大小为i+ min的元素有pCount[i]个
            arr[j++] = i + min;  
    }
    free(pCount);
}