经典排序方法及细节小结(1)
在数据结构的学习中,排序是我们要重点学习的一部分;在掌握几种经典排序算法的同时,我们还要能够根据实际中遇到的情况,结合它们的时间复杂度、空间复杂度、稳定性这几个方面选择最合适的算法。现针对常用的几种经典排序算法及易出错的地方总结如下:
1.插入排序
(1)直接插入排序
直接插入排序是一种最简单的排序方法,其基本思路是:
①将一条记录插入到已排好的有序表中,从而得到一个大小加1的新有序表。
②每一步将一个待排序的数据元素,按其排序码的大小,插入到前面已经排好序的一组元素的合适位置上去
③循环①②步,直到元素全部插完为止。
假使按升序排序 当该序列为逆序时,每次调整都需将每个元素都需移到最前面,是最坏的情况,一共需移(n*(n-1))/2次;而当其序列基本有序,每个元素微调,一共就只需移动n次左右,便达到了最快的O(N)的复杂度。
时间复杂度:最好情况O(N) 最坏的情况O(N*N) 平均情况O(N*N)
容易看出若是相同的元素在排序前后,它们相对位置是没有变化的,所以
稳定性:稳定
代码如下:
void InsertSort(int* arr, size_t length) { assert(arr); for(size_t i = 0; i< length -1; ++i) { int end = i; int tmp = arr[end + 1]; while(end >= 0) { if(arr[end] <= tmp) break; else { arr[end+ 1] = arr[end]; --end; } } arr[end + 1] = tmp; //Print(arr, length); } }
(2)希尔排序
希尔排序是直接插入排序的优化。优化的地方就在于它将待排序的序列分组进行插入排序,每组排好序后,整个序列就能达到基本有序;最后再进行一次直接插入排序即可。 如对下列序列排序:

具体思路:
①每隔gap大小个单位进行分组
②每个组内进行直接插入排序
③整体进行插入排序
注意:插入排序的快慢受序列有序程度影响,而希尔排序由于分组实现了插入排序使得整个序列希尔排序,整体提高了序列的有序度,提高了效率;同时,希尔排序再一个优化就是每次变化着选取gap来进行分组,这样每以gap分组排一次序后,就使序列更加有序,那么下一次再选一个gap分组排序就会更快了;选gap不妨以每次除以3的方式来选得,这样分得的组数就不会太多,或者太少(容易看出来,如果分得的组数太多,就和普通的插入排序没区别了;如果太少同样若如此)。
时间复杂度:最好情况:O(N) 最坏情况:O(N*N) 平均情况:O(log(N^1.3))
从前面容易知道在直接插入排序中,相同元素相对的位置排完序后不会发生改变;而希尔排序在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以稳定性:
稳定性:不稳定
实现代码:
void ShellSort(int* arr, size_t length) { assert(arr && length > 0); int gap = length; while(gap > 1) //gap ==1 时,继续往后走,进行最后一次整体的插入排序 { //gap不能太大 ,太大使得分组太少,和普通插入排序没多大区别 //同理也不能分得太多。 gap = gap/3 + 1; //加1防止gap为0 //预排 将它们分成多个组,组内进行插入排序;使整体基本有序 for(size_t i = 0; i < length - gap; ++i) { int tail = i; int tmp = arr[tail+ gap]; while(tail >= 0) { if(arr[tail] <= tmp) //tail位置处值不大于待插入的值,跳出 break; else { arr[tail+ gap] = arr[tail]; tail-= gap; } } arr[tail + gap] = tmp; } printf("gap %d:", gap); Print(arr, length); } }
gap分趟排序结果:
2.交换排序
(1)冒泡排序
冒泡排序可能是我们最早接触的排序算法,尽管比较简单,但还是注意取有意义的变量名,同时还可以对其进行一点小的优化
思路:
①从第一个元素开始,相邻两元素比较大小,前面元素大(小),两者就交换位置,直到最大(小)的元素排到了最后;
②在剩下的N -1个元素中继续操作①,直到最后剩下一个元素,结束算法
优化:设置一个标志符flag,flag初始值是0,如果在一趟遍历中有出现元素交换的情况,那就把flag置为1。一趟冒泡结束后,检查flag的值。如果flag依旧是0,那这一趟就没有元素交换位置,说明数组已经有序,循环结束。
时间复杂度:最好情况:O(N) 最坏情况:O(N*N) 平均情况:O(N*N)
稳定性:稳定
代码:
void BubbleSort(int* a, size_t length) //冒泡排序 { assert(a); size_t end = length - 1; size_t i = 0; for (; end > 0; --end) { size_t flag = 0; for (i = 0; i < end; ++i) { if (a[i] > a[i + 1]) { Swap(&a[i], &a[i + 1]); flag = 1; } } if (0 == flag) //冒泡一趟,没有发生一次交换,序列有序 break; } }
(2)快速排序
基本思想就是递归分治,假设要排升序,选取一个标准key,将比key小的全部放到key的左边,将比key大的全部放到key右边;确定了key位置,再以这个位置为界限划分左右子区间,依次往后递归。
这里比较困难的地方其实就是实现每一次的单趟排序。总结下来,有以下3中方法来实现单趟排序(个人感觉难度依次往后增加)
(1)挖坑法
思路:
①假使把数组首元素值作基准key,此时数组第一个位置a[left]就相当于一个‘坑’。
②设置两个指针begin和end分别指向数组的首、尾元素。从end开始向左找到一个比key小的值,用它将begin处值覆盖,相当于填‘坑’
③再从begin处往右找一个比key大的值,用其覆盖end处的值,相当于再把右边 ‘坑’填上
④重复②③,begin=end时结束,最后将最后一个‘坑’填上。
如对{5,1,9,3,6,8,0,2,7,5}序列排序的单趟排序过程如图:
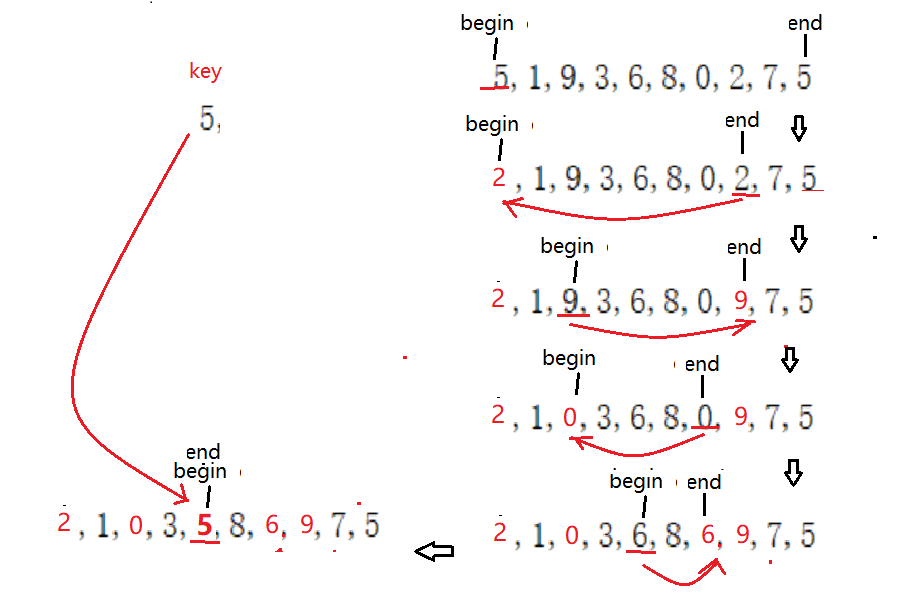
int PartSort1(int* arr, int left, int right) { int tmp= arr[left]; //保存key值 int begin = left; int end = right; while(begin < end) { while(begin < end && arr[end] >= tmp) //找到比key小 --end; arr[begin] = arr[end]; while(begin < end && arr[begin] <= tmp) //找到比key大 ++begin; arr[end] = arr[begin]; } arr[begin] = tmp; //填上最后留下的坑 return begin; }
(2)左右指针法
思路:
①设置两个指针begin和end分别指向数组的首、尾元素,假使选第一个值作为基准值key。
②end依次往左查找比key小的值(先从end处往左找很关键!),begin依次往右查找比key大的值,都找到后就交换两者的值
③继续②至begin = end结束,最后将第一个位置和begin、end最后停下位置处的两个值交换。
注意:
(1)之所以要先从end处往左边找,是由选取的基准值key的位置决定的。如针对序列{6,8,0,2,7},选6为基准key,由于先从end往左找,最后begin、end会在小于key的位置停下 即{6,2,0,8,7} 中'0'的位置;而若先从左边往右找,最后则会停在比key大的位置上 即新序列{6,2,0,8,7}‘8’的位置,最后将6 和 8交换就会出现问题。
(2)基准值key是可以随机选择的。但要考虑到一个问题。随机选择的key值位置如果不是在两端的话,那么实现排序到底是先从begin往右找 还是先从end往左找呢?这有存在问题了,以上面的序列进行分析:
①若选2为key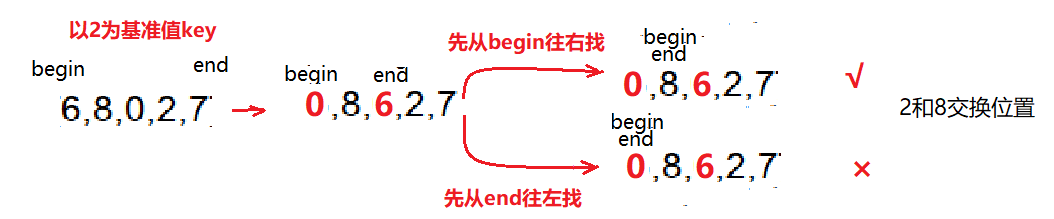
begin end最后停下位置在选的key的左边,因为先从begin往右找,两指针最后会在大于key的位置处停下,故先从begin往右找是不会出错。
②而序列改成{6,7,0,2,8} 此时若选'7'为key,

最后begin end停下位置在key的右边,因为先从end往左找,所以两指针最后会在比较码比key小的位置停下,先从end往右找正确。
所以先从哪边找,要看两指针最后停下的地方是在选定key的位置的左还是右。此处key的位置靠左,所以最后两指针很有可能在其右边停下;而当选定的基准key的位置在序列中间的某个地方时,最后两指针停在那?这就和黑洞样,不得而知了~(说起黑洞,今天得到消息 霍金老先生去了。世界本源无穷尽,我们报以无尽的想象,奈何还是半途终于肉体的结束,)。额....跑远了 继续
细节处理:
比较细节的一步就是先将选的基准key换到最左边位置(或者最右边)这样便可以确定最后两指针停下的位置 避免掉到坑里了。
代码如下:
//左右指针交换法 int PartSort2(int* arr, int left, int right) { //int key = arr[left]; //三数取中法选取key值 //int mid = left + ((right - left)>>1); //int key = GetMidNum(arr[left], arr[mid], arr[right]); //随机数法选key srand(time(NULL)); int index = rand()%(right - left + 1); int key = arr[left + index]; Swap(&arr[left], &arr[left + index]); //细节问题 int begin = left; int end = right; while(begin < end) { while(begin < end && arr[end] >= key) //从右往左找 直到找到比key小的 --end; while(begin < end && arr[begin] <= key) //从左往右找 直到找到比key大的 ++begin; Swap(&arr[begin] , &arr[end]); } //begin end停下位置处值比key小 Swap(&arr[begin], &arr[left]); return begin; }
(3)前后指针法
思路:( 假使排升序)
①选最右边的值作为基准key,设置两个指针cur prev,cur指向开头,prev指向前一个值。
②cur prev依次朝一个方向走,每当cur向后找到比较码比key小的位置,prev找比较码不小于key的位置,交换prev cur处的值
③当cur走到最右边时结束循环,交换最右边和prev+1位置处的值
注意:
1. prev cur是同时往后面走。cur每走过一个比较码大于key的位置就让prev停一次,当cur再走到一个关键码比key小的位置时,prev就恰好在第一个比较码比key大的位置(相当于左边第一个待交换的位置)
2. 由于只有当cur每次走过位置的比较码比key小,prev才往后走;而选arr[right]作key值,故prev最后一定在比较码不小于key的位置停下。因此才有步骤③
(这样这个过程不太好理解,建议将排序的数组定义成全局数组放置开头,在VS等调试器下仔细查看交换过程)
代码:
//前后指针法 //实现单链表的快排 int PartSort3(int* arr, int left , int right) { int prev = left -1; int cur = left; int key = arr[right] ; //选取一个标准 while(cur < right) { if(arr[cur] < key) //cur对应值小于key prev紧随其后 { ++prev; if(prev != cur) //cur对应值>= key,prev不动 cur继续往后找比key小的位置 Swap(&arr[cur], &arr[prev]); //然后交换prev cur两个位置值 } ++cur; } Swap(&arr[++prev], &arr[right]); return prev; }
ps:单链表的快速排序单趟划分能用此种思路。
快排采用了分治思想,用递归里天然的函数栈帧来实现,于是自然就会想到它的非递归实现
快排非递归
用栈来保存每次分治的区间坐标
思路:
①先将最初始的区间坐标压入栈内
②从栈里获得排序序列的区间,再将划分的来到两个子区间压入栈内,当区间长度为1时停止压栈
③重复步骤②,直到栈为空时结束循环
代码:
void QuickSortNonR(int* arr, int left, int right) { assert(arr); if(left >= right) return; Stack s; StackInit(&s); StackPush(&s, left); StackPush(&s, right); while(StackEmpty(&s) != 0) // { int end = StackTop(&s); StackPop(&s); int begin = StackTop(&s); StackPop(&s); int div = PartSort3(arr, begin, end); if(begin < div -1) /左/区间长度大于1 { StackPush(&s, begin); StackPush(&s, div -1); } if(end > div +1) //右区间长度大于1 { StackPush(&s, div+ 1); StackPush(&s, end); } } }
快排的优化
①随机数法:选key时是有可能每次都选到区间的边界值,比如对一个降序序列进行升序排序,每次选得的key就十分尴尬了。随机数法每次随机的选择一个位置的值作key值,这从概率上来讲会提高排序的效率就不言而喻了。
但是即便如此,还是有可能会选到区间两端的值作key,于是又有了下面一种选key的方法
②取中位数法:将区间两端的值和中间位置处的值进行比较,取大小不大不小的数(中位数)作key. 这样进一步提高了效率
③小区间法:切割区间时,当区间内元素数量比较少时就不用切割区间了(递归太深影响效率),这时候就直接对这个区间采用直接插入法,可以进一步提高算法效率。
如果每次选取的key值大小都恰好是序列里中间的值时,那么划分的子区间连接起来就像一颗二叉树一样,
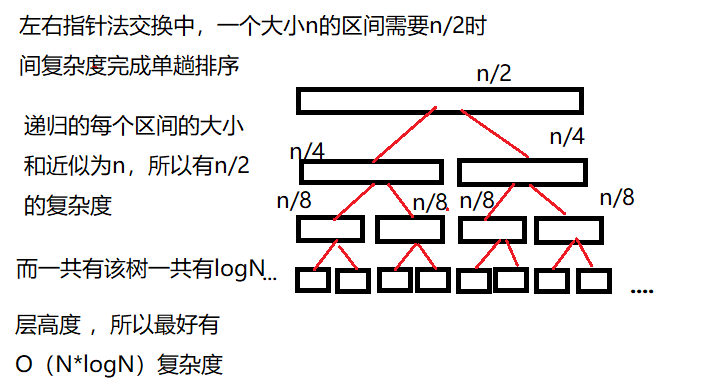
时间复杂度:最好情况:O(NlogN) 最坏:O(N*N) 平均: O(NlogN)
空间复杂度:最好情况:O(logN) 最坏:O(N) (退化为冒泡排序)
稳定性:不稳定
说了这么些,经典的排序算法还有选择排序 归并排序 计数排序 等这么几个排序算法,这里限于篇幅,就下一篇再小结。
同时哪里有不对,也希望能给我指出。乐意讨论~~
本文来自博客园,作者:tp_16b,转载请注明原文链接:https://www.cnblogs.com/tp-16b/p/8555071.html


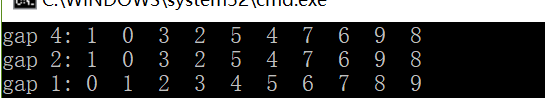

 浙公网安备 33010602011771号
浙公网安备 33010602011771号