二叉树重难点总结(判断完全二叉树,非递归前、中、后序遍历的实现等...)
二叉树是我们在学习数据结构过程中的重难点,这里对其内容稍作总结,巩固自己知识的同时,也希望可以帮助到正在学习此部分内容的同学。废话不多讲,先来做好准备工作,创建好一个二叉树,实现它的一些基本操作。
由于后面实现层次遍历,非递归遍历二叉树时需要用到队列、栈,为实现方便,这里直接把二叉树的定义放到了上次实现的队列、栈的头文件里面( 若有需要:http://www.cnblogs.com/tp-16b/p/8252253.html )。在对应地方作稍作改动(改动地方后面有注释)
StackQueue.h
#ifndef _STACKQUEUE_H_
#define _STACKQUEUE_H_
typedef int BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* _lchild;
struct BinaryTreeNode* _rchild;
BTDataType _data;
}BTNode;
typedef BTNode* SDataType; //栈里存放二叉树结点地址
typedef struct Stack
{
SDataType* _array;
size_t _top; //栈顶
size_t _end;
}Stack;
typedef BTNode* QDataType; //队列里面存放二叉树结点地址
typedef struct QueueNode
{
QDataType _qdata;
struct QueueNode* _next;
}QueueNode;
typedef struct Queue
{
QueueNode* _head;
QueueNode* _tail;
}Queue;
void StackInit(Stack* s);
void StackPush(Stack* s, SDataType x);
void StackPop(Stack* s);
SDataType StackTop(Stack* s);
size_t StackSize(Stack* s);
int StackEmpty(Stack* s);
void QueueInit(Queue* q);
void QueuePush(Queue* q, QDataType x);
void QueuePop(Queue* q);
QDataType QueueFront(Queue* q);
QDataType QueueBack(Queue* q);
size_t QueueSize(Queue* q);
int QueueEmpty(Queue* q);
#endif
二叉树的创建以及普通操作
BinaryTree.c 4 #include<stdio.h> 5 #include<malloc.h> 6 #include<assert.h> 7 #include "StackQueue.h" 8 9 BTNode* BuyBTNode(BTDataType x) { 10 BTNode* newNode = (BTNode*)malloc(sizeof(BTNode)); 11 assert(newNode); 12 13 newNode->_data = x; 14 newNode->_lchild = NULL; 15 newNode->_rchild = NULL; 16 return newNode; 17 } 18 // 创建二叉树 19 BTNode* CreateBTree(BTDataType* a, size_t* pIndex, BTDataType invalid){ 20 assert(a); 21 22 if(a[*pIndex] == invalid){ 23 return NULL; 24 } 25 26 BTNode* root = BuyBTNode( a[*pIndex]); 27 ++*(pIndex); //哇,调好几遍才注意到。不仅是要传Index的指针pIndex,还得注意不是对pIndex++ 28 root->_lchild = CreateBTree(a, pIndex , invalid); 29 ++*(pIndex); 30 root->_rchild = CreateBTree(a, pIndex , invalid); 31 return root; 32 } 33 void BTreePrevOrder(BTNode* root){ //前序遍历 34 if(root == NULL){ 35 return ; 36 } 37 38 printf("%d ",root->_data); 39 BTreePrevOrder(root->_lchild); 40 BTreePrevOrder(root->_rchild); 41 } 42 void BTreeInOrder(BTNode* root){ //中序遍历 43 if(root == NULL){ 44 return ; 45 } 46 47 BTreeInOrder(root->_lchild); 48 printf("%d ",root->_data); 49 BTreeInOrder(root->_rchild); 50 } 51 void BTreePostOrder(BTNode* root) { //后序遍历 52 if(root == NULL){ 53 return; 54 } 55 56 BTreePostOrder(root->_lchild); 57 BTreePostOrder(root->_rchild); 58 printf("%d ",root->_data); 59 }
考察二叉树属性的相关操作
<1>求结点总数 size_t BTreeSize(BTNode* root){ if(root == NULL){ return 0; } //划分子问题 return 1 + BTreeSize(root->_lchild) + BTreeSize(root->_rchild); }
<2>求叶子结点数 size_t BTreeLeafSize(BTNode* root) { if(root == NULL){ return 0; } //该结点的左右子树为空,返回1 if(root->_lchild == NULL && root->_rchild == NULL){ return 1; } return BTreeLeafSize(root->_lchild) + BTreeLeafSize(root->_rchild); } <3>求二叉树的深度
//选左右子树深度较大的递归
size_t BTreeDepth(BTNode* root) { if(root == NULL){ return 0; } size_t leftDepth = BTreeDepth(root->_lchild); size_t rightDepth = BTreeDepth(root->_rchild); if(leftDepth > rightDepth){ //选深度 return leftDepth + 1; } return rightDepth + 1; }
<4>求第K层二叉树的结点数 //转化为k -1层结点数子问题 size_t BTreeKLevelSize(BTNode* root, size_t k){ if(root == NULL || k <= 0){ return 0; } if(root && k == 1){ //到根结点 return 1; } return BTreeKLevelSize(root->_lchild, k-1 ) + BTreeKLevelSize(root->_rchild, k-1 ); }
<5>二叉树查找 BTNode* BTreeFind(BTNode* root, BTDataType x) { if(root == NULL){ return NULL; } if(root->_data == x) return root; //定义变量来保存结果,这样如果在左子树找到了,就不用在去右子树查找,提高了效率 BTNode* lChildRet = BTreeFind(root->_lchild , x); if(lChildRet){ return lChildRet; } BTNode* rChildRet = BTreeFind(root->_rchild , x); if(rChildRet){ return rChildRet; } }
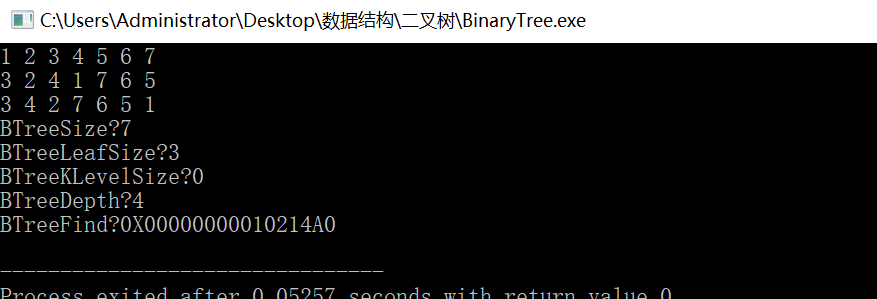
先简单测一下:
void TestBinaryTree0(){
int a[] = {1, 2, 3, '#','#',4,'#', '#', 5, 6,7,'#','#' ,'#' ,'#',};
size_t index = 0;
BTNode* tree = CreateBTree(a, &index, '#');
BTreePrevOrder(tree); printf("\n");
BTreeInOrder(tree); printf("\n");
BTreePostOrder(tree); printf("\n");
printf("BTreeSize?%d\n", BTreeSize(tree));
printf("BTreeLeafSize?%d\n", BTreeLeafSize(tree));
printf("BTreeKLevelSize?%d\n", BTreeKLevelSize(tree, 6));
printf("BTreeDepth?%d\n", BTreeDepth(tree));
printf("BTreeFind?%#p\n", BTreeFind(tree , 6));
}
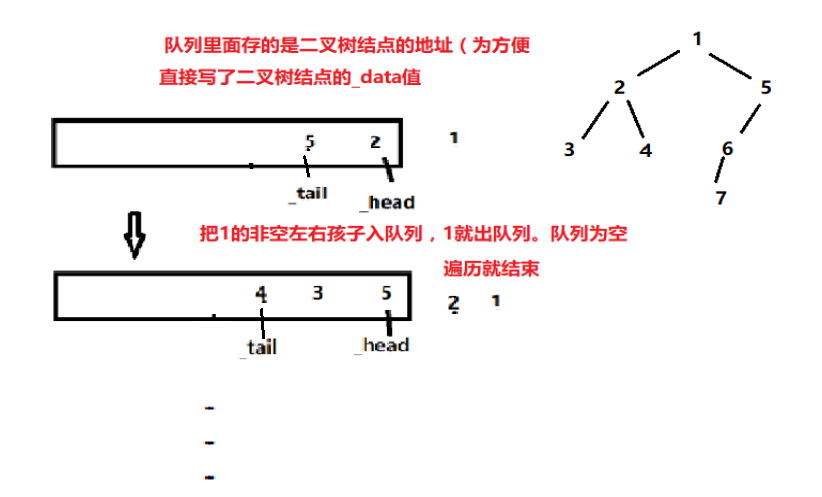
二叉树的层次遍历
思路:借助队列来实现,先把二叉树根结点地址入队列,以后每从队列里面出一个树结点地址,访问该结点的同时将其左右子结点的地址入队列,直到队列为空。
//层次遍历 void BTreeLevelOrder(BTNode* root) { //用队列来实现 if(root == NULL){ return ; } Queue q; QueueInit(&q); QueuePush(&q, root); while(QueueEmpty(&q) != 1){ //QueueEmpty(&q)等于1表示 队列里面为空 //每从队列出一个BTNode* 就将其不为NULL的左右孩子入队列 BTNode* cur = QueueFront(&q); QueuePop(&q); printf("%d ",cur->_data); if(cur->_lchild){ QueuePush(&q , cur->_lchild); } if(cur->_rchild){ QueuePush(&q , cur->_rchild); } } }
借助层次遍历判断完全二叉树的两种方法
先说一下什么是完全二叉树:完全二叉树其实就是其前n层都是满的,且第n层从左往右必须是连续的
<1>第一种方法:按层次遍历的思路,不过要注意的是要把二叉树结点地址为NULL的结点的地址也入队列,最后当队列Pop到QueueFront为NULL时,再去判断队列里面存的是否全为NULL,若不是,就不是完全二叉树。
如下:
int IsCompleteBTree(BTNode* root){
if(root == NULL){ //空树也算完全二叉树
return 1;
}
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while(QueueFront(&q)){ //队列头元素值为NULL时停止
//不管左右子树结点是否为空,都将其入队列
BTNode* cur = QueueFront(&q);
QueuePop(&q);
QueuePush(&q , cur->_lchild);
QueuePush(&q , cur->_rchild);
}
while(QueueEmpty(&q) != 1){
if(QueueFront(&q)){ //队列里面不全是NULL的则判定为其不是完全二叉树
return 0;
}
QueuePop(&q);
}
return 1;
}

因为完全二叉树‘左半’部分是满的,是没有空缺的,这一点在队列很容易体现出来。
<2>再一个方法是添加一个flag标记位来标识同层结点前面是否出现‘‘空缺’(为0表示有‘空缺’,不是完全二叉树)。
具体实现也是借助层次遍历的实现方式,一开始flag置为1;在往后执行的过程中,每从队列出一个结点,就判断往队列里带入该结点的左右子结点是否为空?是空就将flag置0,不是空就再依据当前flag的值来决定是否将左右子结点入队列;如果flag为1,左右子结点入队列,否则,其不是完全二叉树。

int IsCompleteBTree1(BTNode* root){ // flag的方式判断 if(root == NULL){ return 1; } int flag = 1; Queue q; QueueInit(&q); QueuePush(&q , root); while(QueueEmpty(&q) != 1) { //QueueEmpty(&q)等于1 表示队列为空 BTNode* cur = QueueFront(&q); QueuePop(&q); if(cur->_lchild){ if(flag == 0){ // 说明前面已经出现null,不是完全二叉树 return 0; } QueuePush(&q , cur->_lchild); } else{ flag = 0; } if(cur->_rchild){ if(flag == 0){ //前面已经出现null ,不是完全二叉树 return 0; } QueuePush(&q , cur->_rchild); } else{ flag = 0; } } return 1; }
非递归实现二叉树前、中、后序遍历
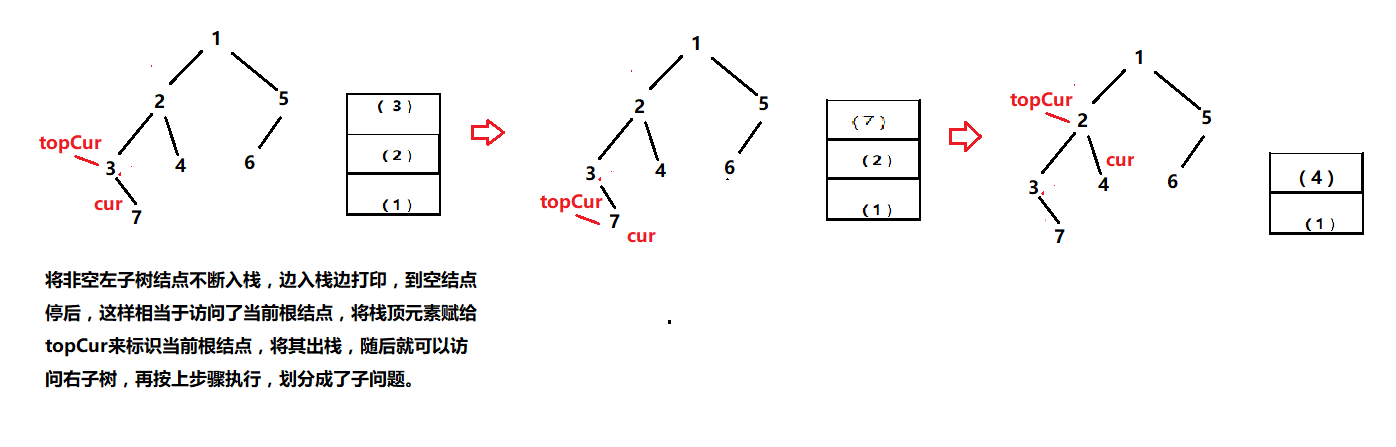
<1>非递归前序遍历:
仿效递归的思路,利用栈来实现的非递归,具体看下图
//非递归前序遍历 void BTreePrevOrderNonR(BTNode* root) { BTNode* cur = root; Stack s; StackInit(&s); BTNode* topCur = NULL; while(cur || !StackEmpty(&s)){ //只有在cur指向了空,同时栈也空的情况下,停止循环。 while(cur){ printf("%d ",cur->_data); StackPush(&s , cur); cur = cur->_lchild; } topCur = StackTop(&s); cur = topCur->_rchild; StackPop(&s); } printf("\n"); }
<2>非递归中序遍历:
和前面的前序遍历十分相似,开始还是将根节点入栈,非空的左子结点不停入栈,到左子结点为空时,访问当前根结点,然后再访问它的右子树,重复以上步骤。
//非递归中序
void BTreeInOrderNonR(BTNode* root){
BTNode* cur = root;
Stack s;
StackInit(&s);
BTNode* topCur = NULL;
while(cur || !StackEmpty(&s)){
while(cur){
StackPush(&s , cur);
cur = cur->_lchild;
}
topCur = StackTop(&s);
printf("%d ",topCur->_data); //访问当前根结点
cur = topCur->_rchild;
StackPop(&s);
}
printf("\n");
}
<3>非递归后序遍历:
和中序遍历一样的思路,只是后序遍历的步骤会稍微繁琐一些。①开始还是将根结点入栈;②非空左子结点不断入栈,③左子结点为空时,就考察当前结点(即栈顶结点)的右子结点是否被访问过, 若已经访问过,则访问当前结点自身,并将其出栈,否则,将该右子结点入栈;如果栈非空就重复②、③直到栈空为止,结束算法。
后序遍历繁琐之处就在于要去判断当前结点的右子树是否被访问过。解决这个问题,有一个办法就是添加一个prev指针来标识上一个访问的结点。
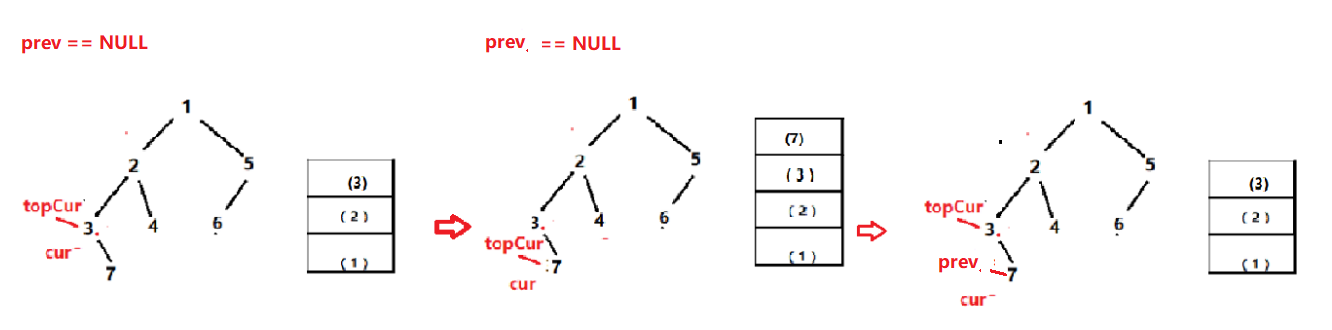
注意:在结点3都入栈后(topCur指向3),由于是后序遍历,此时不能立即就访问结点3,得先去访问它的右子树,等到结点7入栈后,且它的左右子结点为null,那么便可访问结点7,同时让prev指向它,随后结点7出栈;继续循环,然后topCur又指向结点3,但此时prev == topCur->_rchild 这样就说明结点3的右树已经访问过了;然后访问结点3 同时让prev又指向3,3再出栈 .....依次循环,最后便实现了非递归的后序遍历 。
void BTreePostOrderNonR(BTNode* root){
BTNode* cur = root;
Stack s;
StackInit(&s);
BTNode* topCur = NULL;
BTNode* prev = NULL;
while(cur || !StackEmpty(&s)){
while(cur){
StackPush(&s , cur);
cur = cur->_lchild;
}
topCur = StackTop(&s);
//判断右树是否被访问?
if(topCur->_rchild == NULL || topCur->_rchild == prev){ //右子结点为空也记作访问过了
printf("%d ",topCur->_data);
prev = topCur;
StackPop(&s);
}
//右树没有被访问,
else{
cur = topCur->_rchild;
}
}
printf("\n");
}
② 实现后序遍历还有一个比较好理解的方法,那就是利用双栈来实现。先以 根->右->左的先序顺序遍历,其遍历的结果其实就是后序遍历结果的逆序顺序,将遍历结果存放一个栈中后,再利用一个栈将顺序反转过来即可,如此便实现了后序遍历。不足之处就是这样有额外的空间开销。
void BTreePostOrderNonR1(BTNode* root){
if(root == NULL){
return ;
}
BTNode* cur = root;
Stack s;
StackInit(&s);
BTNode* topCur = NULL;
//定义的SaveStack栈来保存后序遍历的逆序结果
Stack SaveStack;
StackInit(&SaveStack);
while(cur || !StackEmpty(&s)){
while(cur){
StackPush(&SaveStack , cur);
StackPush(&s , cur);
cur = cur->_rchild;
}
topCur = StackTop(&s);
StackPop(&s);
cur = topCur->_lchild;
}
//从SaveStack栈里输出
while(!StackEmpty(&SaveStack)) {
printf("%d ",StackTop(&SaveStack)->_data);
StackPop(&SaveStack);
}
printf("\n");
}
菜鸟小结,难免出错 ~ 如若有错,恳求指教。
本文来自博客园,作者:tp_16b,转载请注明原文链接:https://www.cnblogs.com/tp-16b/p/8252319.html