leetcode-机器人的运动范围
1. 题目描述
地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。
例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。
但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？
LeetCode链接： leetcode-机器人的运动范围
示例
输入：m = 2, n = 3, k = 1
输出：3
2. 解题思路
本题与 矩阵中的路径 类似，是典型的搜索 & 回溯问题
方法一： 深度优先搜索+剪枝
-
深度优先搜索： 可以理解为暴力法模拟机器人在矩阵中的所有路径。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
-
剪枝： 在搜索中，遇到数位和超出目标值、此元素已访问，则应立即返回，称为 可行性剪枝 。
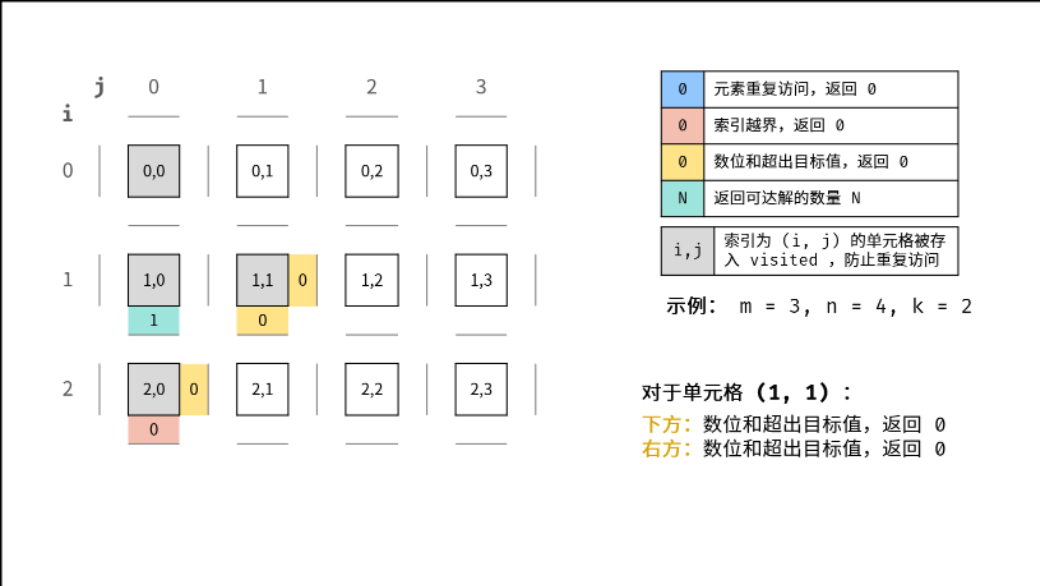
算法解析：
递归参数： 当前元素在矩阵中的行列索引 i 和 j。
终止条件：返回0：
① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过
递推工作：
- 标记当前单元格 ：将索引 (i, j) 存入 Set visited 中，代表此单元格已被访问过。
- 搜索下一单元格： 计算当前元素的 下、右 两个方向元素的数位和，并开启下层递归 。
回溯返回值： 返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数，代表从本单元格递归搜索的可达解总数。
代码实现
class Solution:
def movingCount(self, m: int, n: int, k: int) -> int:
vis =set()
def getSum(num):
res = 0
while num>0:
res += num%10
num = int(num / 10)
return res
def dfs(i,j,k):
if i>=m or j>=n: return 0
if (i,j) in vis: return 0
if getSum(i)+getSum(j)>k: return 0
vis.add((i,j))
return 1+dfs(i+1,j,k) + dfs(i,j+1,k)
return dfs(0,0,k)
方法二：广度优先遍历 BFS
-
BFS/DFS ： 两者目标都是遍历整个矩阵，不同点在于搜索顺序不同。DFS 是朝一个方向走到底，再回退，以此类推；BFS 则是按照[平推]的方式向前搜索。
-
BFS 实现： 通常利用队列实现广度优先遍历。
算法解析：
初始化： 将机器人初始点 (0, 0) 加入队列 queue ；
终止条件： queue 为空。代表已遍历完所有可达解。
迭代工作：
1. 单元格出队： 将队首单元格的 索引、数位和 弹出，作为当前搜索单元格。
2. 判断是否跳过： 若 ① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过 。
3. 标记当前单元格 ：将单元格索引 (i, j) 存入 Set visited 中，代表此单元格 已被访问过 。
4. 单元格入队： 将当前元素的 下方、右方 单元格的 索引、数位和 加入 queue 。
5. 返回值： Set visited 的长度 len(visited) ，即可达解的数量。
代码实现
class Solution:
def movingCount(self, m: int, n: int, k: int) -> int:
queue, visited = [(0, 0, 0, 0)], set()
while queue:
i, j, si, sj = queue.pop(0)
if i >= m or j >= n or k < si + sj or (i, j) in visited: continue
visited.add((i,j))
queue.append((i + 1, j, si + 1 if (i + 1) % 10 else si - 8, sj))
queue.append((i, j + 1, si, sj + 1 if (j + 1) % 10 else sj - 8))
return len(visited)
