leetcode-零钱兑换[322]

题目描述

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。
你可以认为每种硬币的数量是无限的。

 输入：coins = [1, 2, 3], amount = 6
 输出：2 
 解释：6 = 3 + 3

动态规划

我们采用自下而上的方式，仍定义 F(i)F(i) 为组成金额 ii 所需最少的硬币数量，假设在计算 \(F(i)\) 之前，我们已经计算出 $F(0) - F(i-1) $的答案。 则 $F(i) $对应的转移方程应为:

\[F(i)= min_{j = 0...n-1}F(i-c_j)+1 \]

其中，其中\(c_j\)代表的是第 j 枚硬币的面值

示例

\[\begin{aligned} F(3) &=\min \left(F\left(3-c_{1}\right), F\left(3-c_{2}\right), F\left(3-c_{3}\right)\right)+1 \\ &=\min (F(3-1), F(3-2), F(3-3))+1 \\ &=\min (F(2), F(1), F(0))+1 \\ &=\min (1,1,0)+1 \\ &=1 \end{aligned} \]

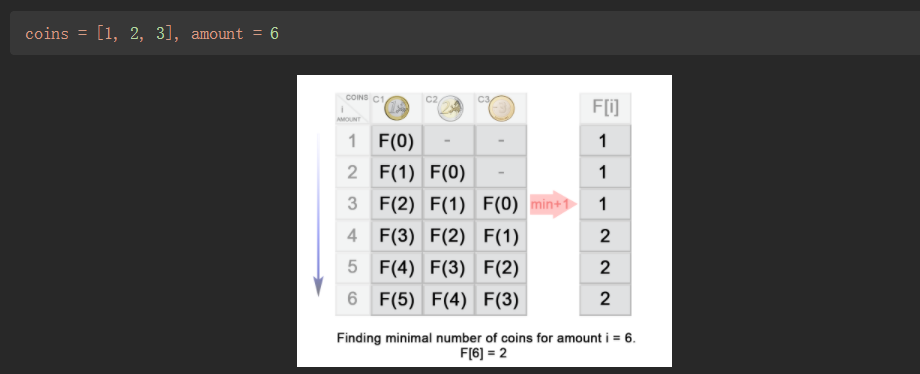
代码实现

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1)
        dp[0] = 0
        
        for i in range(1, amount + 1):
            for coin in coins:
                if coin <=i:
                    dp[i] = min(dp[i], dp[i - coin] + 1)
					
        return dp[amount] if dp[amount] != float('inf') else -1