矩阵分解
矩阵分解-Basic MF
Basic MF是最基础的分解方式,将评分矩阵R分解为用户矩阵U和项目矩阵S, 通过不断的迭代训练使得U和S的乘积越来越接近真实矩阵,矩阵分解过程如图:
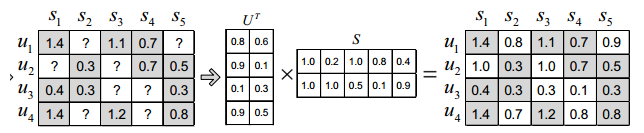
目标函数
预测值与真实值之间的差。采用梯度下降的方式迭代计算U和S,它们收敛时就是分解出来的矩阵。我们用损失函数来表示误差(等价于目标函数):
\[\sum_{i=1}^{n}\sum_{j=1}^{m}(R_{ij}-U^T_iS_j)^2
\]
上式中\(R_{ij}\)为评分矩阵中已知的打分值,\(U_i\)和\(S_j\)是未知变量,为了求上述公式的最小值,相当于求关于U和S二元函数的最小值(极小值),采用梯度下降方法:
梯度下降
\[U_i = U_i - \eta\frac{\partial{L}}{\partial{U_i}} \\
S_j = S_j - \eta\frac{\partial{L}}{\partial{S_j}} \\
\]
正则化矩阵分解-Regularized MF
正则化矩阵分解是Basic MF的优化,解决MF造成的过拟合问题。其不是直接最小化损失函数,而是在损失函数基础上增加规范化因子,将整体作为损失函数。
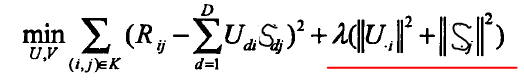
红线表示正则化因子,在求解U和S时,仍然采用梯度下降法,此时迭代公式变为:
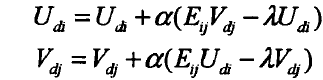
其中,
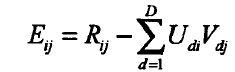


 浙公网安备 33010602011771号
浙公网安备 33010602011771号