算法总结之 将正方形矩阵顺时针转动90度

给定一个 N * N的矩阵，把这个矩阵调整成顺时针转动90度后的形式

  要求额外空间复杂度为O（1）

 

这里仍然使用分圈处理方式

   如果你愿意一层一层一层的拨开我的心~  哈哈哈

   由外到内的旋转

    上代码一目了然：

 

package TT;

public class Test16 {

    public static void rotate(int[][] matrix){
        
        int tR = 0;
        int tC = 0;
        int dR = matrix.length-1;
        int dC = matrix[0].length-1;
        
        while(tR<dR){
            rotateEdge(matrix, tR++, tC++, dR--, dC--);
    
        }
        
    }
    
    
   public static void  rotateEdge(int[][] m ,int tR, int tC, int dR, int dC){
       int times = dC-tC;
       int tmp = 0;
       for(int i =0; i!=times; i++){
           tmp=m[tR][tC+i];
           m[tR][tC+i]=m[dR-i][tC];
           m[dR-i][tC] = m[tR+i][dC];
           m[tR+i][dC] = tmp;
       }
   }
    
    public static void main(String[] args){
        
        int[][] m = new int[3][3];
        m[0][0]=1; m[0][1]=2;m[0][2]=3;
        m[1][0]=4; m[1][1]=5;m[1][2]=6;
        m[2][0]=7;m[2][1]=8;m[2][2]=9;
        
        rotate(m);
        
        System.out.println(m[0][0]);
        System.out.println(m[0][2]);
        
    }
    
    
}

随便抽查了几个数：

正方形的好做很多，正方形的题目比矩形的考虑维度少了一个，就是一行和一列时候的问题

public class Test6 {
    public static int[][] revolveRetangle(int[][] arr) {
        int col = 0;
        int row = 0;
        int endCol = arr[0].length - 1;
        int endRow = arr.length - 1;
        while (row != endRow && col != endCol) { // 控制最外层 到层的走势
            arr = alterPosition(arr, row, endRow, col, endCol);
            row++;
            col++;
            endRow--;
            endCol--;
        }
        return arr;
    }
    // 出来一层  参考系是 天花板那个边上的点
    public static int[][] alterPosition(int[][] arr, int row, int rowEnd, int col, int colEnd) {
        int offset = 0; //定位到要移动的那个元素
        int movPositionLen = rowEnd; //移动多少距离  距离是慢慢缩小的（与具体旋转时候坐标位置相关）
        while (offset<rowEnd) {  //正方形 移动的每个边长的移动寿命都是一样的 没有特殊情况
            //每一次循环 控制的是每一个边上面 点  的移动
            int temp = arr[row+offset][col];
            arr[row+offset][col]=arr[row][col+movPositionLen-offset]; //offset控制的是AD边的移动 (col-offset)是个整体
            arr[row][col+movPositionLen-offset]=arr[row+movPositionLen-offset][col+movPositionLen];
            arr[row+movPositionLen-offset][col+movPositionLen]= arr[row+movPositionLen][col+offset];
            arr[row+movPositionLen][col+offset]=temp;
            offset++;
        }
        return arr;
    }
    public static void main(String[] args) {
        int[][] arr = new int[3][3];
        arr[0][0] = 1;
        arr[1][0] = 2;
        arr[2][0] = 3;
        arr[0][1] = 4;
        arr[1][1] = 5;
        arr[2][1] = 6;
        arr[0][2] = 7;
        arr[1][2] = 8;
        arr[2][2] = 9;
        int[][] result = revolveRetangle(arr);

        for (int i=0; i<result.length; i++){
           for (int j=0; j<result[i].length; j++){
               System.out.print(result[i][j]+",");
           }
        }
    }
}

我解释下吧，这样小伙伴们容易理解

画个图：

  

 

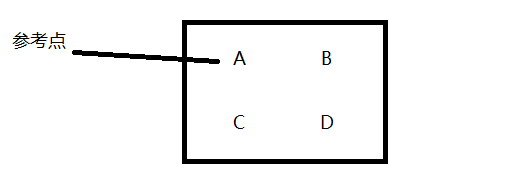
 由于是顺时针移动 每个点的移动范围是有限制的  而且都是一个坐标不变 改变另一个坐标   offset记录的是每一次移动的点滴 移动后就是另一帮点 在做交换了

 并且 当用A的位置作为参考系时候 它交给了temp 

谁来取代他 然后反推就可以知道了 反推出那个坐标 所以设置了个movPositionLen 变量 因为每次反推时候 是需要有变化的

小伙伴们 懂我的意思了吗？如果你们有更好的思路私信我哈~