外部排序---置换选择+败者树

　　当需要对一个大文件进行排序时，计算机内存可能不够一次性装入所有数据，解决办法是归并。归并的大概做法是将大文件分为若干段，依次读入内存进行排序，排序后再重新写入硬盘。这些排好序的片段成为顺串。然后对这些顺串进行逐躺归并，使归并段逐渐由小变大，最终使整个文件有序。要使用归并就得考虑两个问题，一个是如何生成顺串，一个是如何对顺串进行归并。

置换选择算法

　　先考虑如何生成顺串。我们知道，减少顺串的数量可以降低归并的次数，而在文件大小固定的情况下，要减少顺串的数量，就要增大单个顺串的长度。如果使用内部排序生成顺串，那么顺串的大小最多等于可用内存的大小。因此我们使用置换选择排序，可以生成大概两倍于内存大小的顺串。步骤如下：

　　（1）首先从输入文件中读取N个数字将数组填满　　

　　（2）使用数组中现有数据构建一个最小堆

 

　　（3）重复以下步骤直到堆的大小变为0：

 

　　　　a. 把根结点的数字A（即当前数组中的最小值）输出

 

　　　　b. 从输入文件中再读出一个数字B，若R比刚输出的数字A 大，则将B放到堆的根节点处，若B不比A大，则将堆的最后一个元素移到根结点，将B放到堆的最后一个位置，并把堆的大小缩减1（即新读入的数据没有进入堆中）

 

　　　　c. 在根结点处调用Siftdown重新维护堆

 

　　（4）换一个输出文件，重新回到步骤（2）

书上有个铲雪机的例子来类比证明出使归并段长度的期望值为两倍工作区容量，但我觉得类比说明不了什么问题，严谨的证明我又不会，就跳过吧。

败者树

　　接下来考虑如何对顺串进行归并。多路归并排序算法在常见数据结构书中都有涉及。从2路到多路（k路），增大k可以减少归并趟数，外存信息读写时间，但k个归并段中选取最小的记录需要比较k-1次，为得到u个记录的一个有序段共需要(u-1)(k-1)次，若归并趟数为s次，那么对n个记录的文件进行外排时，内部归并过程中进行的总的比较次数为s(n-1)(k-1)，也即

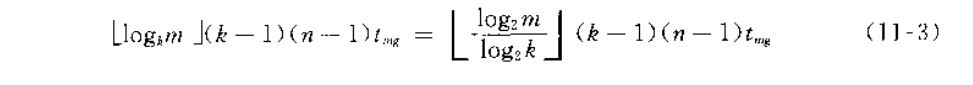
而(k-1)/logk随k增而增因此内部归并时间随k增长而增长了，抵消了外存读写减少的时间，这样做不行，由此引出了“败者树”的使用。败者树只需进行logk次比较，在内部归并过程中利用败者树将k个归并段中选取最小记录比较的次数降为(logk)次使总比较次数为(logm)(n-1)，与k无关。

败者树的具体操作《数据结构》书里有，我就不赘述了。这里说一下败者树和堆的比较。

堆执行一次比较（即调整）时间复杂度也是logn，但是堆调整的时候父节点要分别和两个子节点进行比较，而败者树只需和兄弟节点进行一次比较即可。因为要存储败者信息，败者树占用空间会比堆大。