基于js 实现 小球来回滚动动画
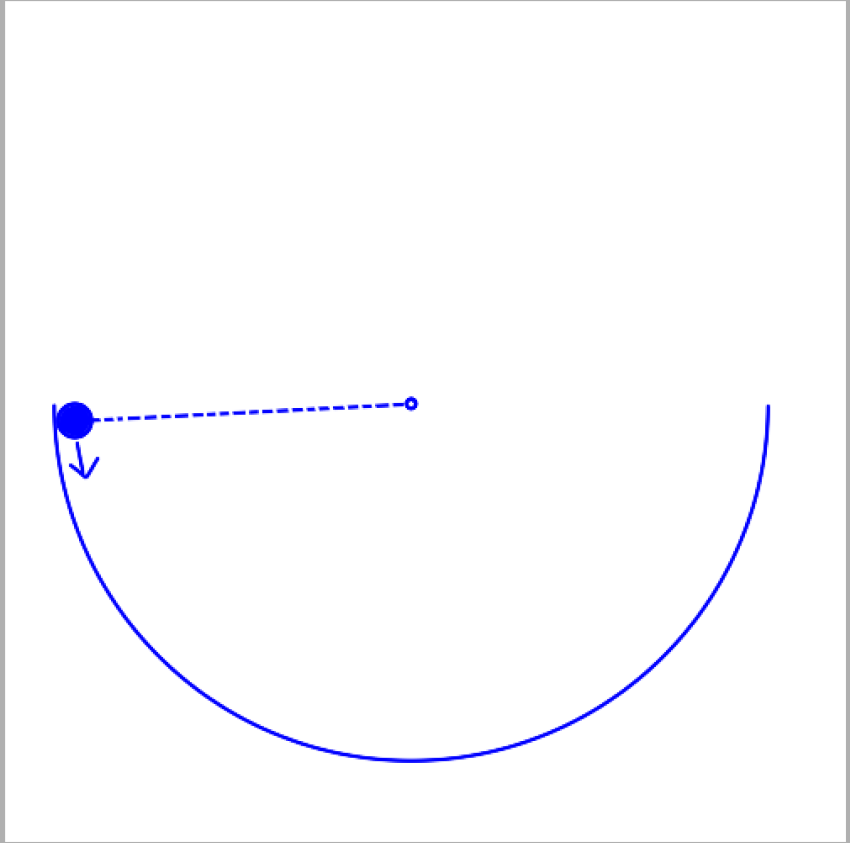
我们依靠js能否实现小球左右来回摆动的动画，实际是可以的
现在我们来分析一下，需要怎么实现，众所知周，这是一个物理问题，我们应该从物理的角度出发去解决这个问题，我们知道圆周运动 肯定涉及到牛顿运动定律，那么以下公式成立
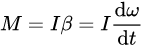.................................................................①
对于题设，我们需要知道的是他绕中心转动，此时中心和他之间的连接我们默认质量无限趋向于0，那么就可以计算转动惯量：
.......................................................②
我们又知道 转动惯量矩是重力执行的结果，所以可以算出转动惯量矩如下
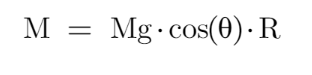..............................③
我们带入公式1可以得出 角加速度的值:
.............................④
我们又知道 角加速度存在以下关系:
.................................................⑤
我们带入④中可以得到：
...................................⑥
ok，现在我们已经清楚了 旋转角的微分方程，那么现在摆在我们面前有2条路，第一条路是利用计算机强大的性能根据上面的公式模拟出真实世界的物体运动过程，第二条路是硬解上面的微分方程得出时间和旋转角的关系，
我们先来看第一种：
我们知道 积分的原理是很微小的部分慢慢叠加的，只要我们用计算机正确设计模拟出比较靠谱的微小，那么就能够比较像的模拟真实的物理过程，我们分步来 第一次，如下
解释上述为 w表示此刻的角速度，△t表示 我们所定义的微小时间量 θ0表示0时刻此时的旋转角度，那么根据第一次的结果，我们可以计算出下一次的如下
当然下一次又在上一次的基础上进行计算，所以我们先将这一切转换为计算机语言：
let β = 0, w = 0, θ = 0, r = 2/100, deltat = 5/1000, g=9.8;
上述中的r表示半径 deltat表示△t，g表示重力加速度，
那么我们用什么来迭代呢，js为我们提供了非常棒的setInerval方法如下
setInterval(()=>{ let row = document.getElementsByClassName('rows')[0] β = g*Math.cos(θ)/r; w = w + β*deltat; θ = θ + w*deltat; console.log(β,w,θ,`${(θ/(Math.PI/2))*90}`) row.style.transform = `rotate(${(θ/(Math.PI/2))*90}deg)` },16.6)
上述表达了我们将通过设置div的rotate来进行模拟，那么最终的效果如下：
可以看到还是比较像的 但是在真实环境中 感觉似乎还差点什么，那说明你感觉对了 我们是没16.6毫秒迭代 0.005秒，但是在真实世界中，时间的流动是那么的自然，自然到我们现在没办法评估到底要多小的无穷小量才能正确模拟
。我们可以做一个验证，将迭代间隔改为0.001秒 同时将△t改为0.001s 那么这时候看起来就非常像了
但是下面这种同样也存在问题，这意味着每千分之1秒我们需要计算一次，同时还要让计算的结果成功绘制到界面上，这对计算机的性能消耗似乎很大，所以我们还是采用第一种比较稳妥
现在我们来讲讲第二种，我们知道 上面方程为
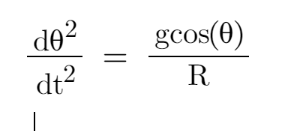
现在我们利用walfram alpha 计算上述方程的解：
有图可知 笔者也看不懂am函数的具体表达式，有兴趣的朋友可以试试，
结语：那么我们现在评估一下2种方式的优点 第一种 简单 不需要函数的解，直接带入时间进行迭代，但是问题是迭代的精度不高，可能造成拟合不好，提高迭代精度的话，又可能造成计算性能消耗，所以只能折中点，第二种方法就不一样了，他直接解除θ和时间的关系，也就是说我们可以知道任何一个时刻θ的位置，不能说精确，但是精确度肯定是比第一种高很多的，难就难在对结果方程的认知上
好了，that'all thank you,cheers 🍺🍺🍺🍺🍺🍺🍺🍺
源码如下:
<html>
<head>
<meta charset="utf-8" />
<meta content="telephone=no" name="format-detection" />
<meta
content="width=device-width, initial-scale=1, maximum-scale=1, minimum-scale=1, user-scalable=no"
name="viewport"
/>
<meta content="no-cache" http-equiv="pragma" />
<meta
content="no-cache, no-store, must-revalidate"
http-equiv="cache-control"
/>
<meta content="0" http-equiv="expires" />
<link href="data:;base64,=" rel="icon" />
</head>
<style>
.rows {
width:100px;
height:10px;
transform: rotate(0deg);
transform-origin: 0 5px;
margin-left:100px;
display:flex;
justify-content:flex-end;
}
.dot {
width:10px;
height:10px;
border-radius: 5px;
background:blue;
}
.head {
position:absolute;
left: 100px;
top: 10px;
width:10px;
height:10px;
border-radius: 5px;
background:blue;
}
</style>
<body>
<div class="head"></div>
<div class="rows">
<div class="dot"></div>
</div>
</body>
<script>
// 100px约等于2cm
let β = 0,
w = 0,
θ = 0,
r = 2/100,
deltat = 1/1000,
g=9.8;
setInterval(()=>{
let row = document.getElementsByClassName('rows')[0]
β = g*Math.cos(θ)/r;
w = w + β*deltat;
θ = θ + w*deltat;
console.log(β,w,θ,`${(θ/(Math.PI/2))*90}`)
row.style.transform = `rotate(${(θ/(Math.PI/2))*90}deg)`
},1)
</script>
</html>
