unity中模拟弹簧的力-受力分析

水平放置一个弹簧，压缩，后面有一个球，放开球之后，求球的位移 速度 时间的关系

解： 假设弹簧的任意位置在x处，弹簧为压缩状态为x0，弹簧的初始化位置为0

则根据牛顿第二定律，列出微分方程：

    F = k(x0 - x)

    F = m*dv/dt => F = m*x''

    k(x0 - x) = m*x''

   规范化该方程可得

 m*x'' + 0*x' + kx - kx0 = 0

发现为二阶常系数微分方程，可在walfram alpha中求解：

 

 带入初始化条件 X|_t=0 = 0和X'|_t=0 = 0 可以得到

 X(t) = X0 - X0*cos((k/m)^0.5*t)......................................(1)

 V(t) = X' = X0*(k/m)^0.5*sin((k/m)^0.5*t).......................(2)

可通过能量守恒定律验证上述结果： 即

k*x0*x - 0.5*k*x^2 = 0.5*m*v^2

=> 带入(1)和(2) 会发现方程左右两边相等

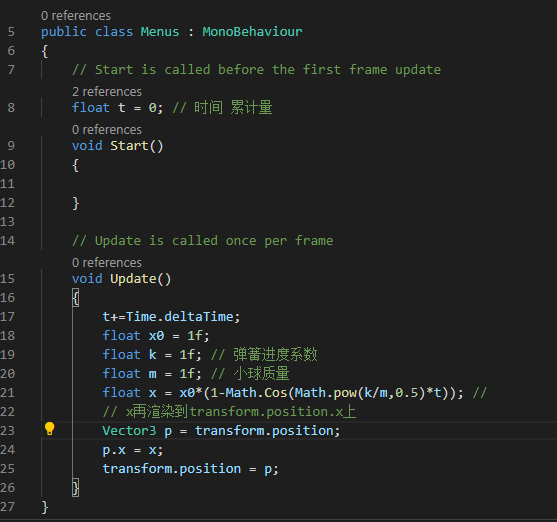
将上述结果带入Unity的c#中....