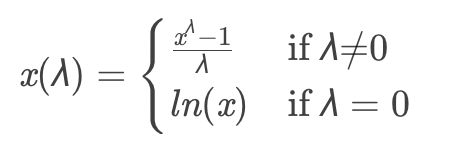特征预处理——特征缩放

特征缩放（Feature Scaling）是一种将数据的不同变量或特征的方位进行标准化的方法。

在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲（数量级）的纯数值，便于不同单位或量级的指标能够进行比较和加权。

特征缩放的好处：

参考：标准化的好处及常见处理方法

1. 提升模型的收敛速度

2.提升模型的精度

3.深度学习中数据归一化可以防止模型梯度爆炸。

需要特征缩放的模型：

参考：哪些机器学习模型需要归一化

概率模型（树形模型）不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、RF（随机森林）、朴素贝叶斯、XGBoost、lightGBM、GBDT

而像Adaboost、SVM（支持向量机）、LR（线性回归、逻辑回归）、KNN、KMeans、神经网络（DNN、CNN和RNN）、LSTM之类的最优化问题就需要归一化

特征缩放的方法：

常用的特征缩放的方法有归一化、标准化、正态化等。参考：2(1).数据预处理方法

选择建议：

参考：标准化和归一化什么区别？ 和 机器学习 | 数据缩放与转换方法（1）

1.特征是正态分布的，使用z-score标准化

2.特征不是正态分布的，可以尝试使用正态化（幂变换）

3.特征是正态分布的，如果有离群值，可以使用RobustScaler；没有离群值且是稀疏数据，可以使用归一化（如果数据标准差很小，min-max归一化会比z-score标准化好）

4.先划分训练集和测试集，然后再使用相同的标准化公式对训练集和测试集进行特征缩放

参考：数据的标准化 和 数据预处理（一）：标准化，中心化，正态化

1.归一化（scaler）

1.min-max归一化

也叫离差标准化，是对原始数据的线性变换，将数据统一映射到[0,1]区间上，转换函数如下：

其中max为样本数据的最大值，min为样本数据的最小值。这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。

min-max归一化的特点：

• 缩放到0和1之间
• 目的是使各个特征维度对目标函数的影响权重是一致的
• 不改变其数据分布的一种线性特征变换

min-max归一化的适用场景：

• 如果对输出结果范围有要求，用归一化
• 如果数据较为稳定，不存在极端的最大最小值，用归一化

from sklearn.preprocessing import MinMaxScaler

transfer = MinMaxScaler(feature_range=[0, 1])  # 范围可改变，若不写，默认为0-1
data_minmax = transfer.fit_transform(train_data[["SalePrice"]])
print(data_minmax)

[[0.24107763]
 [0.20358284]
 [0.26190807]
 ...
 [0.321622  ]
 [0.14890293]
 [0.15636717]]

图片转自：https://www.zhihu.com/people/sun_shuai_

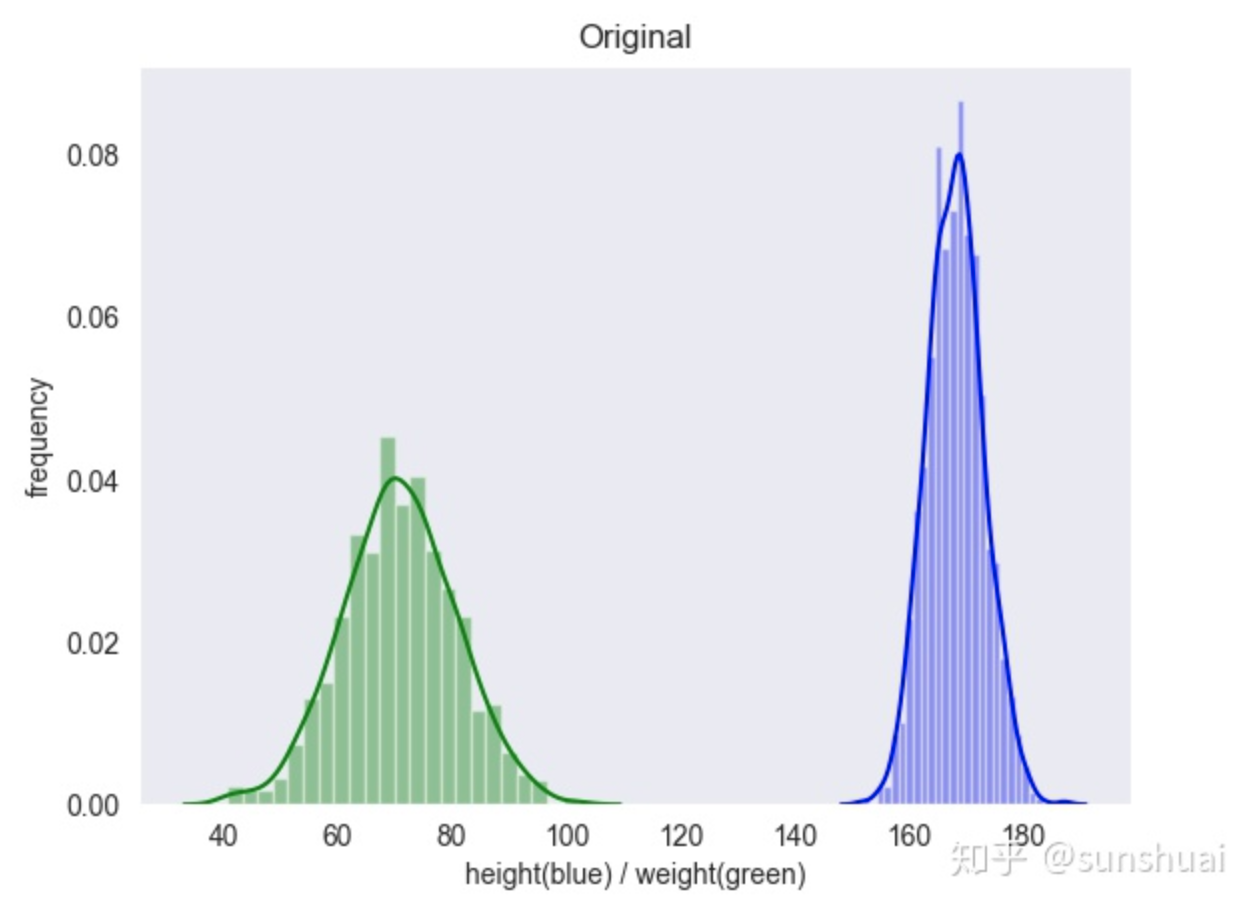
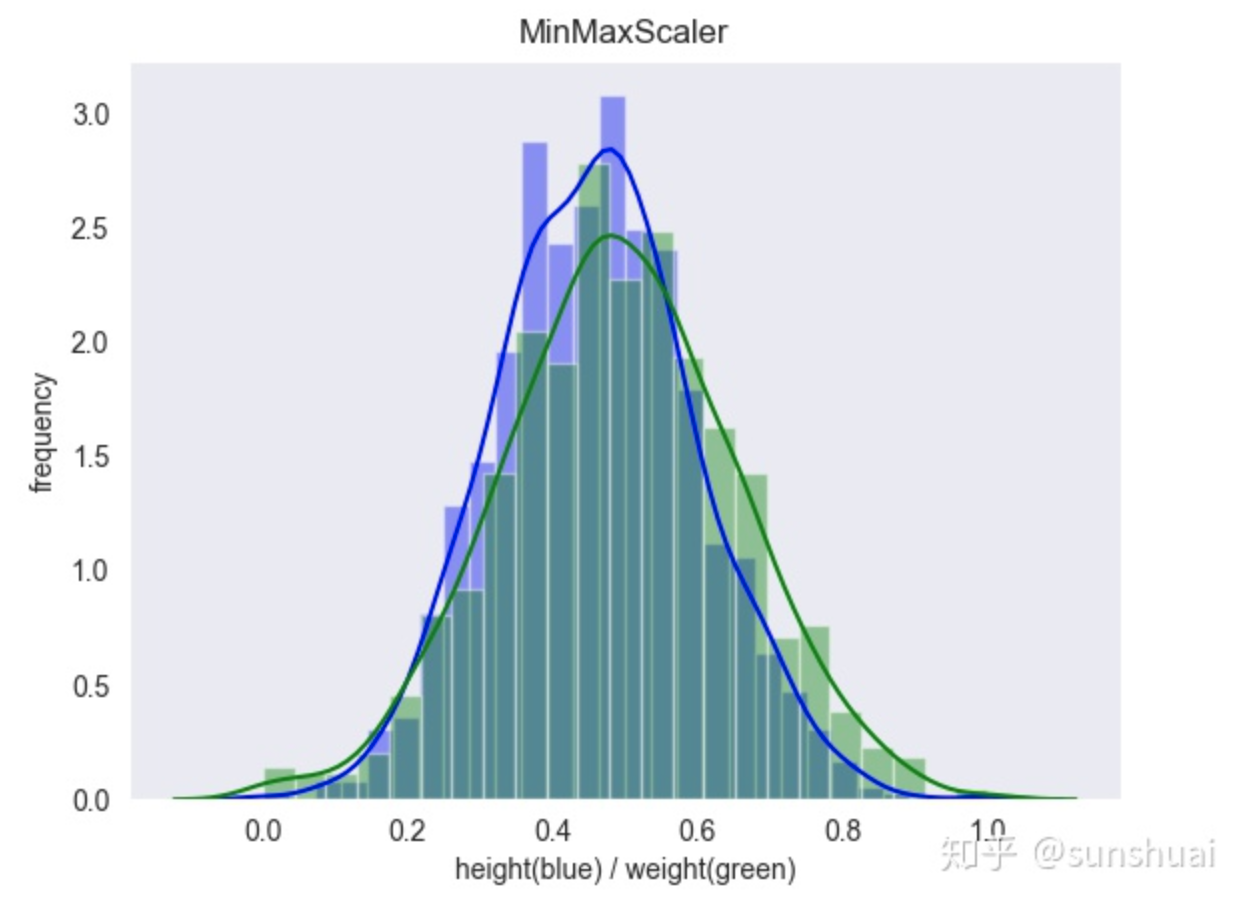
2.MaxAbs归一化

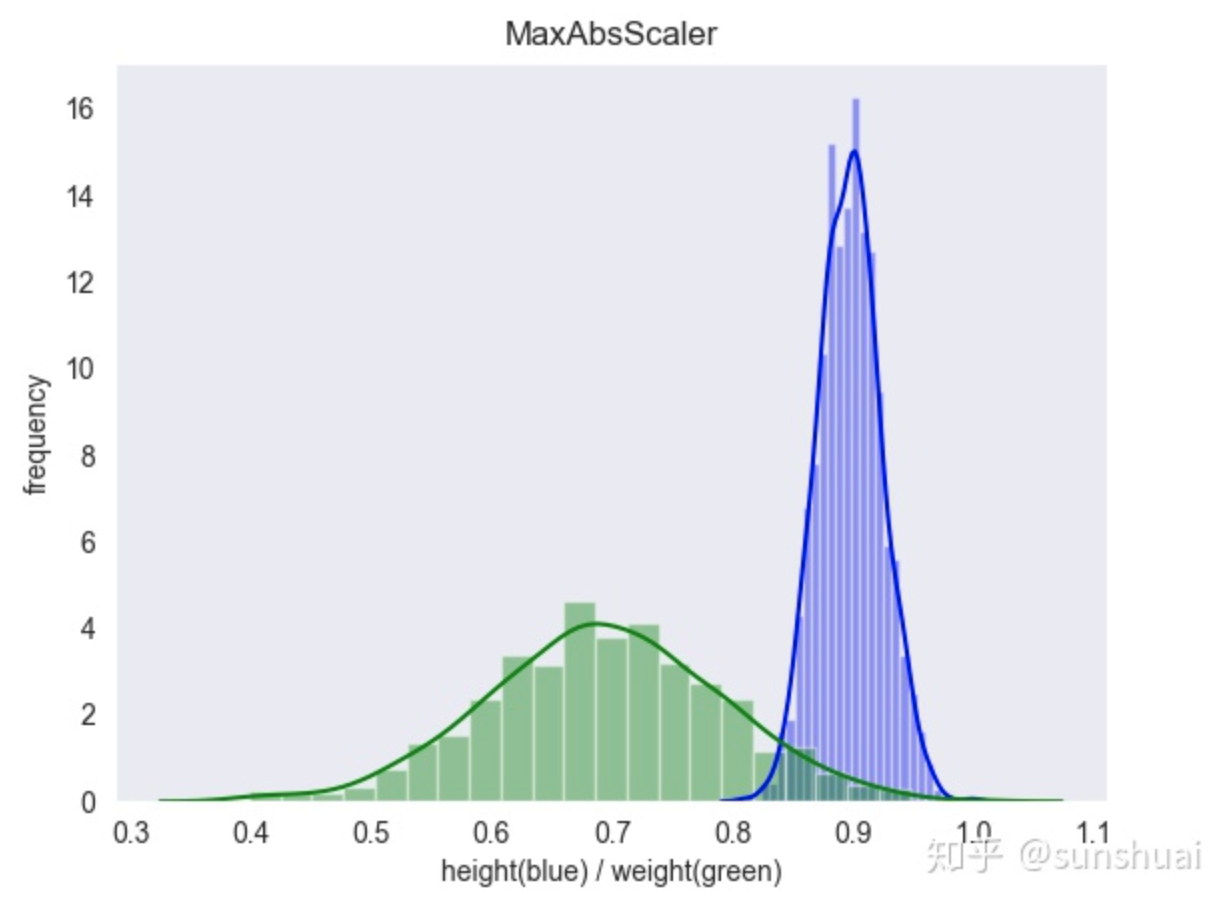
最大值绝对值标准化(MaxAbs)即根据最大值的绝对值进行标准化，假设原转换的数据为x，新数据为x'，那么x'=x/|max|，其中max为x所在列的最大值

MaxAbs归一化的特点：

• MaxAbs方法跟Max-Min用法类似，也是将数据落入一定区间，但该方法的数据区间为[-1,1]
• 不改变其数据分布的一种线性特征变换

MaxAbs归一化的适用场景：

• MaxAbs也具有不破坏原有数据分布结构的特点，因此也可以用于稀疏数据、稀疏的CSR或CSC矩阵。

from sklearn.preprocessing import MaxAbsScaler

transfer = MaxAbsScaler() 
data_minmax = transfer.fit_transform(train_data[["SalePrice"]])
print(data_minmax)

图片转自：https://www.zhihu.com/people/sun_shuai_

2.标准化（standardization）

1.z-score标准化

也叫标准差标准化，经过处理的数据符合均值为0，标准差为1，其转化函数为：

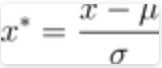
其中μ为所有样本数据的均值，σ为所有样本数据的标准差。

z-score标准化的特点：

• 假设数据是正态分布
• 将数值范围缩放到0附近，数据变成均值为0，标准差为1的正态分布
• 不改变原始数据的分布

z-score标准化的适用场景：

• 这种标准化方法适合大多数类型的数据，也是很多工具的默认标准化方法。如果对数据无从下手可以直接使用标准化；
• 如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响
• 需要使用距离来度量相似性的时候：比如k近邻、kmeans聚类、感知机和SVM，或者使用PCA降维的时候，标准化表现更好
• Z-Score方法是一种中心化方法，会改变稀疏数据的结构，不适合用于对稀疏数据做处理。（稀疏数据是指绝大部分的数据都是0，仅有少部分数据为1）。在很多时候，数据集会存在稀疏性特征，表现为标准差小。并有很多元素的值为0.最常见的稀疏数据集是用来做协同过滤的数据集，绝大部分的数据都是0，仅有少部分数据为1。对稀疏数据做标准化，不能采用中心化的方式，否则会破坏稀疏数据的结构。参考：Python数据标准化

可以使用sklearn的StandardScaler函数对特征进行z-score标准化，注意fit_transform函数的输入需要时2D array

from sklearn.preprocessing import StandardScaler

# z-score标准化
transfer = StandardScaler()
data_standard=transfer.fit_transform(train_data[["SalePrice"]])
print(data_standard)

[[ 0.34727322]
 [ 0.00728832]
 [ 0.53615372]
 ...
 [ 1.07761115]
 [-0.48852299]
 [-0.42084081]]

# 描述性统计
print(pd.DataFrame(data_standard).describe())

count  1.460000e+03
mean   1.362685e-16
std    1.000343e+00
min   -1.838704e+00
25%   -6.415162e-01
50%   -2.256643e-01
75%    4.165294e-01
max    7.228819e+00

可以看到使用z-score标准化后的数据，均值接近0，标准差接近1

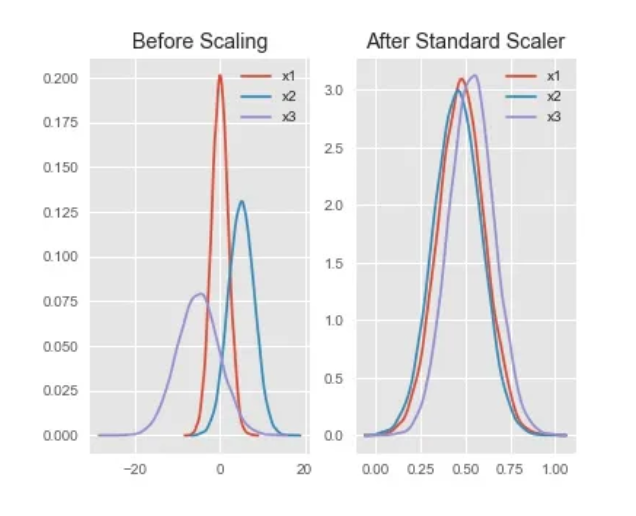
2.RobustScaler

RobustScaler的适用场景：

• 某种情况下，假如数据集中有离群点，我们可以使用Z-Score进行标准化，但是标准化之后的数据并不理想，因为异常点的特征往往在标准化之后便容易失去离群特征。此时可以使用RobustScaler针对离群点做标准化处理，该方法对数据中心化和数据的缩放健壮性有更强的参数控制能力。
• 如果要最大限度保留数据集中的异常，使用RobustScaler方法。

如果数据集包含较多的异常值，可以使用RobustScaler方法进行处理，它可以对数据集的中心和范围进行更具有鲁棒性的评估，如下

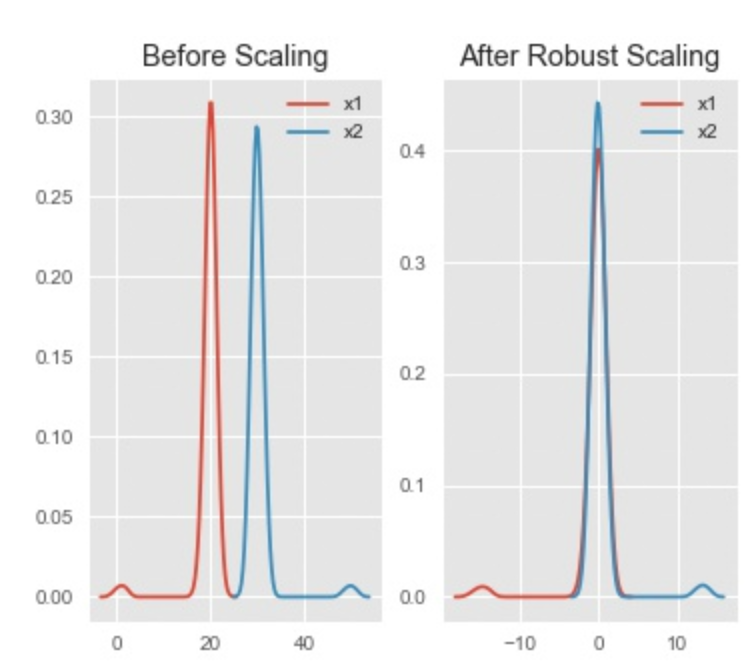
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
from sklearn.preprocessing import RobustScaler

# Robust
transfer = RobustScaler()
data_robust = transfer.fit_transform(train_data[["SalePrice"]])
sns.distplot(pd.DataFrame(data_robust), fit=norm)
print(pd.DataFrame(data_robust).describe())
plt.show()

3.幂变换（Power Transform）

常用的幂变换包括：对数变换，box-cox变换，指数变换等，属于非线性变换

PowerTransformer 目前提供两个这样的幂变换, Yeo-Johnson transform 和 the Box-Cox transform。其中 Box-Cox 仅能应用于严格的正数，Yeo-Johnson 可以是正数也可以是负数

1.Yeo-Johnson标准化：

其转化函数为：

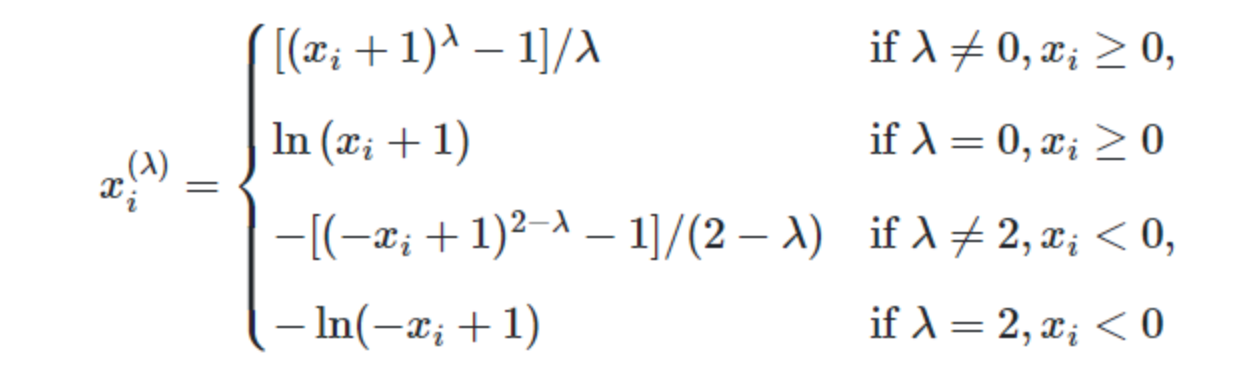
data_yeojohnson = preprocessing.PowerTransformer(method='yeo-johnson', standardize=False)

2.box-cox标准化：

Box-Cox转换法是幂变换中最受欢迎的方法，用于连续的响应变量不满足正态分布的情况，其通过对原始分布改变其lambda (λ)，将非正态数据转换为正态数据，lambda (λ)是我们自己决定的参数，用于得到最适合的转换效果。

Box-Cox变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效的。其转化函数为：

在进行Box-Cox转换之前，原始数据Y需要全部为正数。如果不是正数，那么添加一个常数C，再进行转换 。

# box-cox, 返回2个值，第二个值是最佳_lambda
data_boxcox, _lambda = stats.boxcox(train_data["SalePrice"])
print(_lambda)
sns.distplot(data_boxcox, fit=norm)
print(pd.DataFrame(data_boxcox).describe())
plt.show()

或者

data_boxcox = preprocessing.PowerTransformer(method='box-cox', standardize=False)

3.log对数函数变换

通过log函数转换的方法同样可以实现正态化，具体方法如下：Y(x)=ln(x)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm

# log
sns.distplot(np.log(train_data[["SalePrice"]]), fit=norm)
print(np.log(train_data[["SalePrice"]]).describe())
plt.show()

4.分位数转化（Quantile Transform）

QuantileTransformer 是一种非参数的数据转化技术，可以将数据转化到特定的分布（一般是高斯分布或者均匀分布），通过分位数函数来实现。

这是一种非线性变换。QuantileTransformer类将每个特征缩放在同样的范围或分布情况下。但是，通过执行一个秩转换能够使异常的分布平滑化，并且能够比缩放更少地受到离群值的影响。但是它的确使特征间及特征内的关联和距离失真了。参考：参考：sklearn中常用的特征预处理方法（scaler）

from sklearn.preprocessing import QuantileTransformer

# Quantile Transform
quantile_transformer = QuantileTransformer(random_state=0,  output_distribution='normal')

5.正则化（normalization）

1.normalizer

参考：数据转化 和 机器学习 | 数据缩放与转换方法（1）

正则化的过程是将每个样本缩放到单位范数（每个样本的范数为1），如果后面要使用如二次型（点积）或者其它核方法计算两个样本之间的相似性这个方法会很有用。

Normalization主要思想是对每个样本计算其p-范数，然后对该样本中每个元素除以该范数，这样处理的结果是使得每个处理后样本的p-范数（l1-norm,l2-norm）等于1。p-范数的定义为：

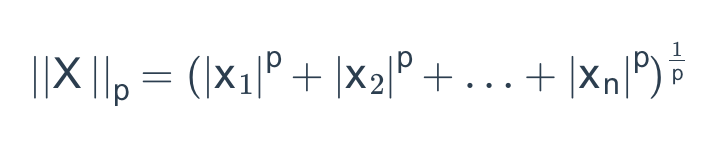
normalizer归一化的特点：

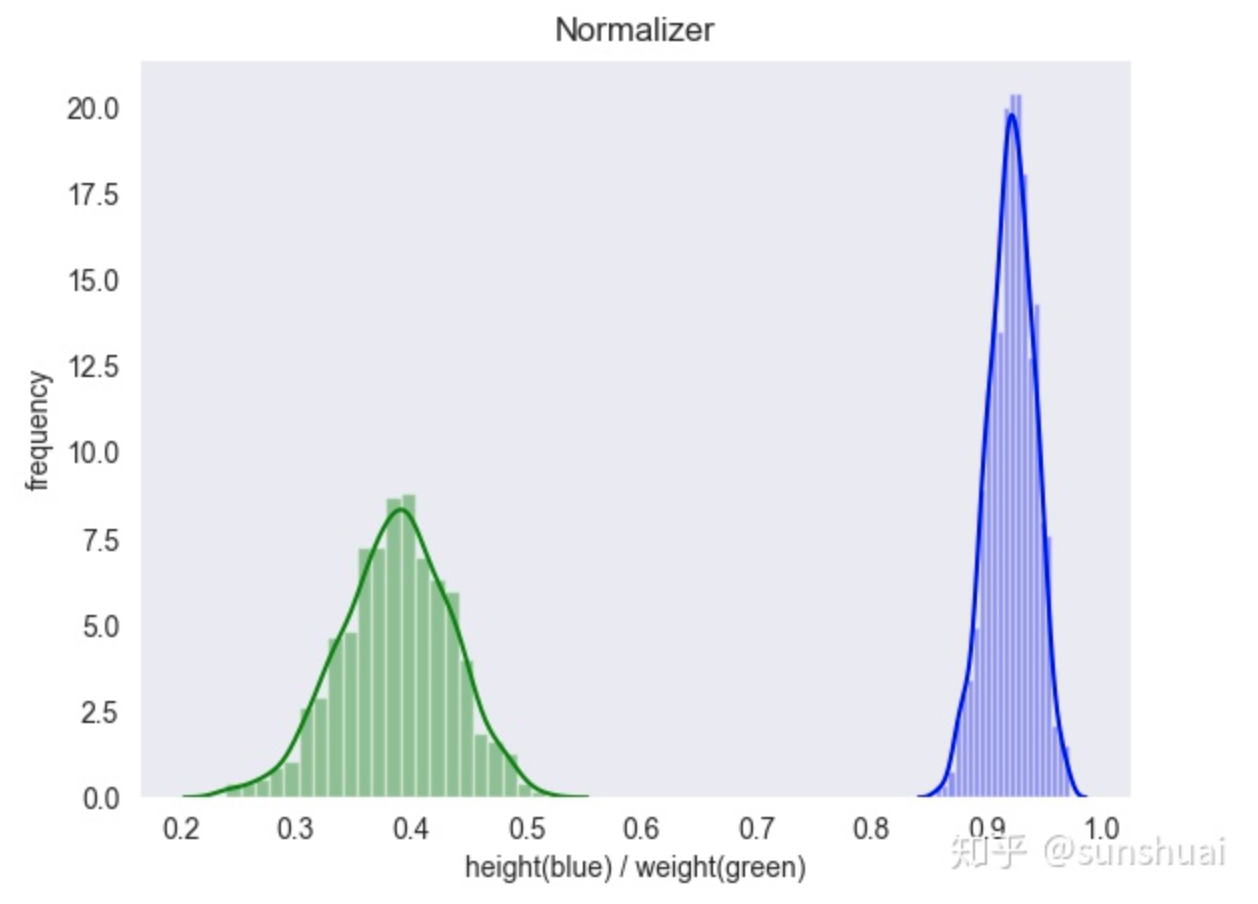
• 缩放到0和1之间，保留原始数据的分布

normalizer归一化的使用场景：

• 该方法主要应用于文本分类和聚类中。例如，对于两个TF-IDF向量的l2-norm进行点积，就可以得到这两个向量的余弦相似性。

sklearn 中有两种方法可以进行 Normalization：normalize 函数和 Normalizer 类，可以通过 norm 参数指定使用的范数类型（l1,l2,max）

from sklearn.preprocessing import Normalizer

transfer = Normalizer() 
data_normal = transfer.fit_transform(train_data[["SalePrice"]], norm='max')
print(data_normal)

图片转自：https://www.zhihu.com/people/sun_shuai_