机器学习——决策树

1.决策树的构造

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据

缺点：可能会产生过度匹配问题

适用数据类型：数值型和标称型

 

# coding:utf-8
# !/usr/bin/env python

'''
Created on Oct 12, 2010
Decision Tree Source Code for Machine Learning in Action Ch. 3
@author: Peter Harrington
'''
from math import log
import operator

#通过是否浮出水面和是否有脚蹼，来划分鱼类和非鱼类
def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing','flippers']
    #change to discrete values
    return dataSet, labels

def calcShannonEnt(dataSet):	#计算给定数据集的香农熵
    numEntries = len(dataSet)	#数据集中的实例总数
    labelCounts = {}
    #为所有可能的分类创建字典，键是可能的特征属性，值是含有这个特征属性的总数
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    #计算香农熵
    shannonEnt = 0.0
    #为所有的分类计算香农熵
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) 	#以2为底求对数
    #香农熵Ent的值越小，纯度越高，即通过这个特征属性来分类，属于同一类别的结点会比较多
    return shannonEnt
    
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     #chop out axis used for splitting
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
    
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      #the last column is used for the labels
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):        #iterate over all the features
        featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
        uniqueVals = set(featList)       #get a set of unique values
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy     #calculate the info gain; ie reduction in entropy
        if (infoGain > bestInfoGain):       #compare this to the best gain so far
            bestInfoGain = infoGain         #if better than current best, set to best
            bestFeature = i
    return bestFeature                      #returns an integer

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList): 
        return classList[0]#stop splitting when all of the classes are equal
    if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]       #copy all of labels, so trees don't mess up existing labels
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree                            
    
def classify(inputTree,featLabels,testVec):
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    key = testVec[featIndex]
    valueOfFeat = secondDict[key]
    if isinstance(valueOfFeat, dict): 
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat
    return classLabel

def storeTree(inputTree,filename):
    import pickle
    fw = open(filename,'w')
    pickle.dump(inputTree,fw)
    fw.close()
    
def grabTree(filename):
    import pickle
    fr = open(filename)
    return pickle.load(fr)
    
    
if __name__ == '__main__':
    myDat,labels = createDataSet()
    print myDat
    print calcShannonEnt(myDat)
	

 

 

#通过是否浮出水面和是否有脚蹼，来划分鱼类和非鱼类
def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing','flippers']
    #change to discrete values
    return dataSet, labels

def calcShannonEnt(dataSet):	#计算给定数据集的香农熵
    numEntries = len(dataSet)	#数据集中的实例总数
    labelCounts = {}
    #为所有可能的分类创建字典，键是可能的特征属性，值是含有这个特征属性的总数
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    #计算香农熵
    shannonEnt = 0.0
    #为所有的分类计算香农熵
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) 	#以2为底求对数
    #香农熵Ent的值越小，纯度越高，即通过这个特征属性来分类，属于同一类别的结点会比较多
    return shannonEnt

 

myDat,labels = createDataSet()
print myDat
print calcShannonEnt(myDat)

 

 

2.划分数据集

def splitDataSet(dataSet, axis, value):		#按照给定特征划分数据集，axis表示根据第几个特征，value表示特征的值
    retDataSet = []				#创建新的list对象
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     #切片
            reducedFeatVec.extend(featVec[axis+1:])	#把序列添加到列表reducedFeatVec中
            #print reducedFeatVec
            retDataSet.append(reducedFeatVec)		#把对象reducedFeatVec（是一个list）添加到列表retDataSet中
    return retDataSet

 

def chooseBestFeatureToSplit(dataSet):		#选择最好的数据集划分方式
    numFeatures = len(dataSet[0]) - 1      	#特征的数量，最后一列是标签，所以减去1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1	#信息增益和最好的特征下标
    for i in range(numFeatures):        	#递归所有特征
        featList = [example[i] for example in dataSet]	#创建一个列表，包含第i个特征的所有值
        uniqueVals = set(featList)       	#创建一个集合set，由不同的元素组成
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)	#按照所有特征的可能划分数据集
            prob = len(subDataSet)/float(len(dataSet))		#计算所有特征的可能性
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy     #计算信息增益
        if (infoGain > bestInfoGain):       	#比较不同特征之间信息增益的大小
            bestInfoGain = infoGain         	#选取信息增益大的特征
            bestFeature = i
    return bestFeature                      	#返回特征的下标

 

3.递归构建决策树

 

def createTree(dataSet,labels):		#创建决策树的函数，采用字典的表示形式
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList): 	#如果类别完全相同则停止继续划分
        return classList[0]
    if len(dataSet[0]) == 1: 					#遍历完所有特征时返回出现次数最多的
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)		#选择信息增益最大的特征下标
    bestFeatLabel = labels[bestFeat]				#选择信息增益最大的特征
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])					#从标签中删除已经划分好的特征
    featValues = [example[bestFeat] for example in dataSet]	#取得该特征的所有可能取值
    uniqueVals = set(featValues)				#建立一个集合
    for value in uniqueVals:
        subLabels = labels[:]       
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)	#递归createTree
    return myTree  

 

myDat,labels = createDataSet()
myTree = createTree(myDat,labels)
print myTree

{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

 

 

4.在Python中使用Matplotlib注解绘制树形图

myDat,labels = createDataSet()
print myDat
import treePlotter
treePlotter.createPlot(myTree)　　#绘制树形图

 

 

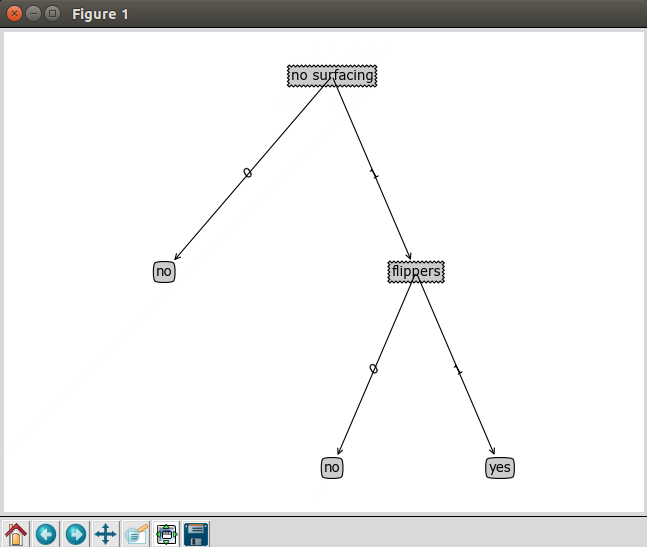
5.构造注解树

 获取叶节点的数目和树的层数

import matplotlib.pyplot as plt

decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")

def getNumLeafs(myTree):		#获取叶子节点的数目
    numLeafs = 0
    firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':	#测试节点的数据类型是否为字典
            numLeafs += getNumLeafs(secondDict[key])	#递归
        else:   numLeafs +=1				#如果不是字典，则说明是叶子节点
    return numLeafs

def getTreeDepth(myTree):		#获取树的层数
    maxDepth = 0
    firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':	#测试节点的数据类型是否为字典，如果不是字典，则说明是叶子节点
            thisDepth = 1 + getTreeDepth(secondDict[key])	#递归
        else:   thisDepth = 1				
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

 绘制树形图

 

 

def plotNode(nodeTxt, centerPt, parentPt, nodeType):	#绘制带箭头的注解
    #annotate参数：nodeTxt：标注文本，xy：所要标注的位置坐标，xytext：标注文本所在位置，arrowprops：标注箭头属性信息
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
             xytext=centerPt, textcoords='axes fraction',
             va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
    
def plotMidText(cntrPt, parentPt, txtString):		#在父子节点间填充文本信息
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

def plotTree(myTree, parentPt, nodeTxt):		#if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  			#计算宽与高
    depth = getTreeDepth(myTree)
    firstStr = myTree.keys()[0]     			#the text label for this node should be this
    print plotTree.xOff
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    print parentPt
    print cntrPt
    plotMidText(cntrPt, parentPt, nodeTxt)		#标记子节点属性值
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD	#减少y偏移
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':	#test to see if the nodes are dictonaires, if not they are leaf nodes   
            plotTree(secondDict[key],cntrPt,str(key))        #recursion
        else:   #it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#if you do get a dictonary you know it's a tree, and the first element will be another dict

def createPlot(inTree):			#绘制树形图，调用了plotTree()
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
    #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
    plotTree.totalW = float(getNumLeafs(inTree))	#存储树的宽度
    plotTree.totalD = float(getTreeDepth(inTree))	#存储树的深度
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5,1.0), '')
    plt.show()

 

 

测试和存储分类器

1.测试算法：使用决策树执行分类

def classify(inputTree,featLabels,testVec):	#使用决策树的分类函数
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)	#将标签字符串转换为索引
    key = testVec[featIndex]
    valueOfFeat = secondDict[key]
    if isinstance(valueOfFeat, dict): 
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat
    return classLabel

 

    myDat,labels = createDataSet()
    Labels = labels
    print "myDat="
    print myDat
    print "labels="
    print labels

    import treePlotter
    myTree = treePlotter.retrieveTree(0)	#绘制树形图
    print myTree
    print classify(myTree,Labels,[0,1])

 

 2.使用算法：决策树的存储

def storeTree(inputTree,filename):	#使用pickle模块存储决策树
    import pickle
    fw = open(filename,'w')
    pickle.dump(inputTree,fw)
    fw.close()
    
def grabTree(filename):			#查看决策树
    import pickle
    fr = open(filename)
    return pickle.load(fr)

 

    myDat,labels = createDataSet()
    Labels = labels
    print "myDat="
    print myDat
    print "labels="
    print labels
    import treePlotter
    myTree = treePlotter.retrieveTree(0)	#绘制树形图
    print myTree
    storeTree(myTree,'classifierStorage.txt')
    print grabTree('classifierStorage.txt')

 

示例：使用决策树预测隐形眼镜类型

 

    import treePlotter
    import simplejson
    import ch
    ch.set_ch()
    from matplotlib import pyplot as plt
    fr = open('lenses.txt')
    lenses = [inst.strip().split('\t') for inst in fr.readlines()]	#读取一行数据，以tab键分割并去掉空格
    lensesLabels = [u'年龄',u'近远视',u'散光',u'眼泪等级']			#使用unicode，不然编码会报错
    lensesTree = createTree(lenses,lensesLabels)
    print simplejson.dumps(lensesTree, encoding="UTF-8", ensure_ascii=False)	#使用simplejson模块输出对象中的中文
    treePlotter.createPlot(lensesTree)