机器学习——分类和回归
1.机器学习的主要任务:
一是将实例数据划分到合适的分类中,即分类问题。 而是是回归, 它主要用于预测数值型数据,典型的回归例子:数据拟合曲线。
2.监督学习和无监督学习:
分类和回归属于监督学习,之所以称之为监督学习,是因为这类算法必须直到预测什么,即目标变量的分类信息。
对于无监督学习,此时数据没有类别信息,也不会给定目标值。在无监督学习中,将数据集合分成由类似的对象组成的多个类的过程被成为聚类;将寻找描述数据统计值的过程称之为密度估计。此外,无监督学习还可以减少数据特征的维度,以便我们可以使用二维或者三维图形更加直观地展示数据信息。

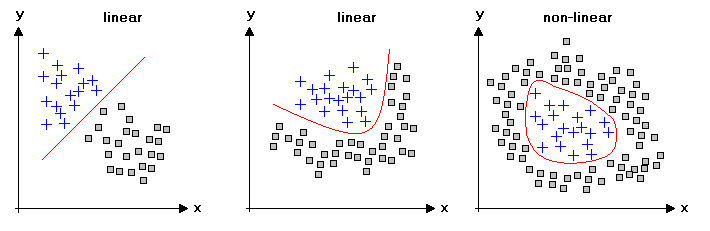
3.线性回归和非线性回归
线性回归需要一个线性模型。一个线性的模型意味着模型的每一项要么是一个常数,要么是一个常数和一个预测变量的乘积。一个线性等式等于每一项相加的和。等式:
Response = constant + parameter * predictor + ... + parameter * predictor <=> Y = b o + b1X1 + b2X2 + ... + bkXk
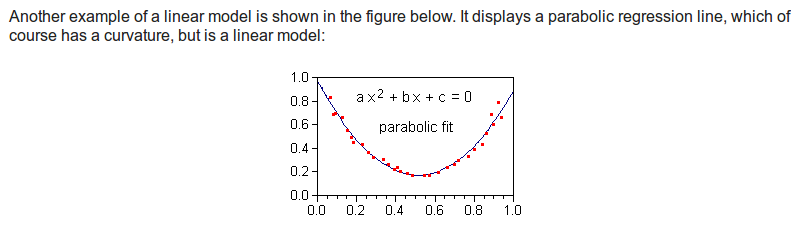
在统计学中,如果一个回归方程是线性的,那么它的参数必须是线性的。但是可以转换预测变量加上平方,来使得模型产生曲线,比如 Y = b o + b1X1 + b2X12
这时模型仍然是线性的,虽然预测变量带有平方。当然加上log或者反函数也是可以的。
另外可以参考的博文:Khan公开课 - 统计学学习笔记:(九)线性回归公式,决定系数和协方差
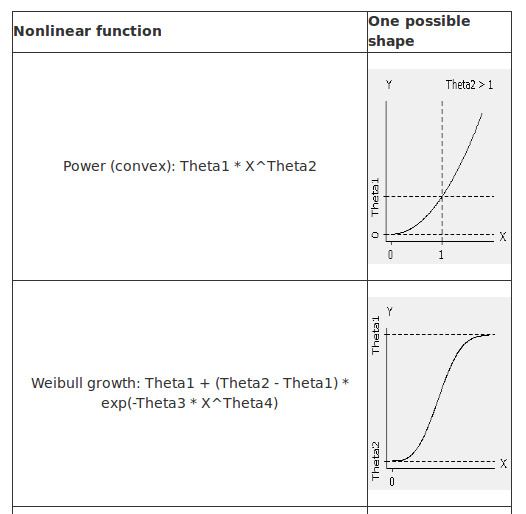
线性回归等式有一个基本的形式,而非线性回归提供了许多灵活的曲线拟合方程。以下是几个MATLAB中的典型非线性方程例子。
非线性函数的一个例子就是高阶多项式(即多项式阶数p>1):G = a o + a1X + a2X^2+ ... + akX^k。其他类型的非线性函数可通过泰勒展开用多项式逼近表示。函数G在x0处的线性近似为G(x0)+G'(x0)(x-x0)。

本文只发表于博客园和tonglin0325的博客,作者:tonglin0325,转载请注明原文链接:https://www.cnblogs.com/tonglin0325/p/6044882.html



