Java数据结构——哈夫曼树（Huffman Tree）

1.哈夫曼树

给定N个权值作为N个叶子节点，构造一棵二叉树，若该树的带权路径长度（WPL）达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。

哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

参考：霍夫曼树（参考该文章中的概念，其中代码不对）

2.树的带权路径长度（WPL，Weighted Path Length of Tree）

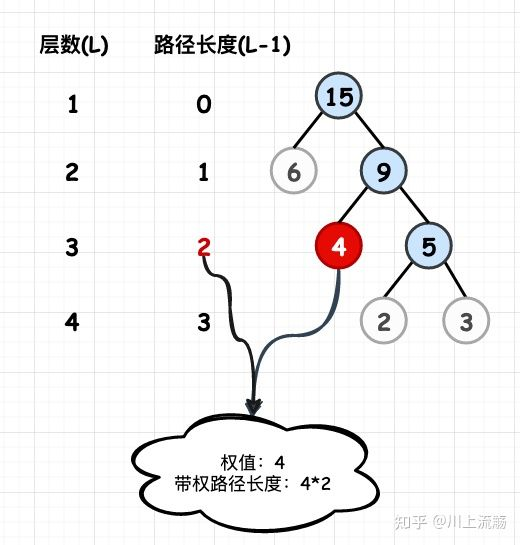
树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）

如下图中的哈夫曼树，其WPL的值 = (2+3) * 3 + 4 * 2 + 6 * 1 = 29

上图参考：数据结构——哈夫曼树（Huffman Tree）

3.哈夫曼树的应用

1.哈夫曼编码

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。

在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。传送报文时总是希望总长度尽可能短。在实际应用中，各个字符的出现频度或使用次数是不相同的，如A、B、C的使用频率远远高于X、Y、Z，自然会想到设计编码时，让使用频率高的用短码，使用频率低的用长码，以优化整个报文编码。如下图

4.哈夫曼编码的实现

1.哈夫曼编码的步骤：

1. 根据输入的字符构建哈夫曼树
   1. 统计原始数据中各字符出现的频率；
   2. 所有字符按频率降序排列；
   3. 建立哈夫曼树：
2. 遍历哈夫曼树并为字符分配code
   1. 将哈夫曼树存入结果数据；
   2. 重新编码原始数据到结果数据

2.建立哈夫曼树的步骤：

1. 初始化：由给定的 N 个权值构造 N 棵只有一个根节点的二叉树，得到一个二叉树集合 。
2. 选取与合并：从二叉树集合 PriorityQueue 中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
3. 删除与加入：从 PriorityQueue 中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到 PriorityQueue 中。
4. 重复 2、3 步，当集合中只剩下一棵二叉树时，这棵二叉树就是霍夫曼树。

3.代码实现：

下面的2个网站中的实现都差不多，都借助了优先队列来进行排序（java是PriorityQueue，python是heapq）

java实现：https://www.geeksforgeeks.org/huffman-coding-greedy-algo-3/

python实现：huffman_tree.py