P1119 灾后重建

历程

• 裸dijkstra \(O(QN^2)\)，TLE
• 堆优化dijkstra \(O(QMlogN)\)，TLE
• floyd \(O(QN^3)\)，TLE
• floyd第一次优化 $O(QN^3) $, TLE
• floyd第二次优化 \(O(N^3)\), WA
• floyd第二次优化改写 \(O(N^3)\), AC

开始妄想用dijkstra堆优化水过，结果T了。。。

题意

给出n个受损村庄分别编号0~n - 1，所有村庄同时开始修，给出每一个村庄的维修时间，接下来进行q次询问（超时的原因），每次询问给出(x, y, t)，需要输出在t天的时候x和y之间的最短距离。

floyd算法

floyd算法用的是动态规划的思路。

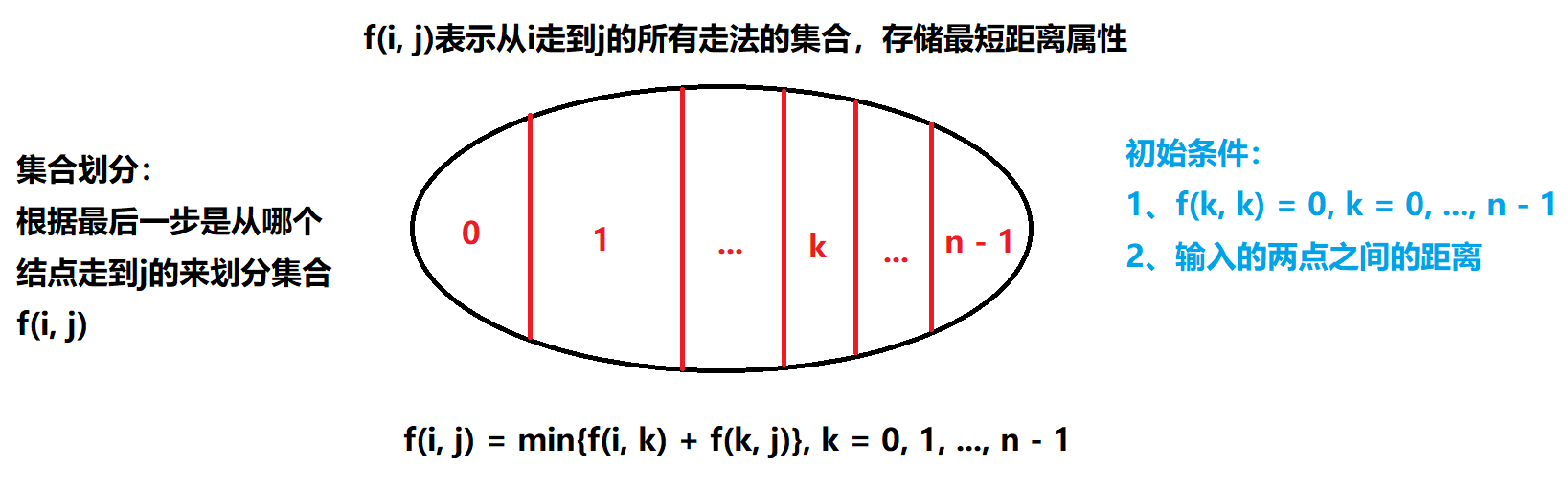
floyd算法可以用来求：在任意一个中转点k（k = 0~n - 1）之下，图的任意两点之间的最短路，自然用floyd就可以求在前k个点作为中转点的影响下的最短距离。

思路

由于本题村庄0~n - 1的维修时间是递增的，并且q个顺序给出的查询中的时间也是递增的，所以可以根据询问所给出的时间t，用floyd将所有维修时间小于等于t的村庄之间的最短距离更新一下，直到t比n - 1号村庄的时间还大为止。

也就是说会根据询问给出的时间t，查看新加入了哪些点，依次用这些点去更新最短距离，直到n个点全部加完。

#include<iostream>
#include<cstring>

using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int g[N][N];
int t[N];
int n, m, q;

int main(){
    memset(g, 0x3f, sizeof g);
    
    cin >> n >> m;
    
    for(int i = 0; i < n; i ++){
        cin >> t[i];
        g[i][i] = 0;
    }
    
    while(m --){
        int a, b, w;
        
        cin >> a >> b >> w;
        g[a][b] = g[b][a] = w;
    }
    
    cin >> q;
    
    int k = 0;
    
    while(q --){
        int x, y, tt;
        
        cin >> x >> y >> tt;
        
        while(k < n && t[k] <= tt){
            for(int i = 0; i < n; i ++)
                for(int j = 0; j < n; j ++)
                    g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
            k ++;
        }
        
        if(g[x][y] == INF || t[x] > tt || t[y] > tt) puts("-1");// 这里注意要特判，t[x]和t[y]和tt的关系，因为可能会把g[x][y]更新小了
        else cout << g[x][y] << endl; 
    }
    
    return 0;
}