波动数列

\[\begin{array} \ 设集合D = \{a, -b\},首项为x.\\ S = x + (x + d_1) + (x + d_1 + d_2) + (x + d_1 + d_2 + d_3) + ... + (x + ... + d_{n-1})\\ \ \ \ = nx + (n - 1)d_1 + (n - 2)d_2 + ... + d_{n-1}(d_k \in D) \\ 即x = (S - [(n - 1)d_1 + (n - 2)d_2 + ... + d_{n-1}]) / n\\ 此时问题转换为选择n-1个d使得[(n - 1)d_1 + (n - 2)d_2 + ... + d_{n-1}] = S (mod \ n) \\ 如果暴力枚举，那么每个d有两种选择，复杂度为O(2^n),2^{1000}超时\\ 所以考虑dp\\ 注意：此处对d_1到d_{n - 1}的不同看法可以有两种做法，一种是dp，还有一种是记忆化，这两种的状态转移矩阵完全相同。\\ dp做法：\\ 由于d_1到d_{n - 1}都是未知数，所以可以把b_i和b_{n - i}交换，从而变成找n-1个d使\\ [d_1 +2d_2 + ... + (n - 1)d_{n-1}] = S (mod \ n)的所有情况数(这个操作保证了最优子结构的) \\记忆化做法：\\直接记忆化搜索，不用改变式子，状态转移矩阵的更新顺序同dp\\ 注意本题还有负数取模，还要自己写取模函数 \end{array} \]

dp分析方法：

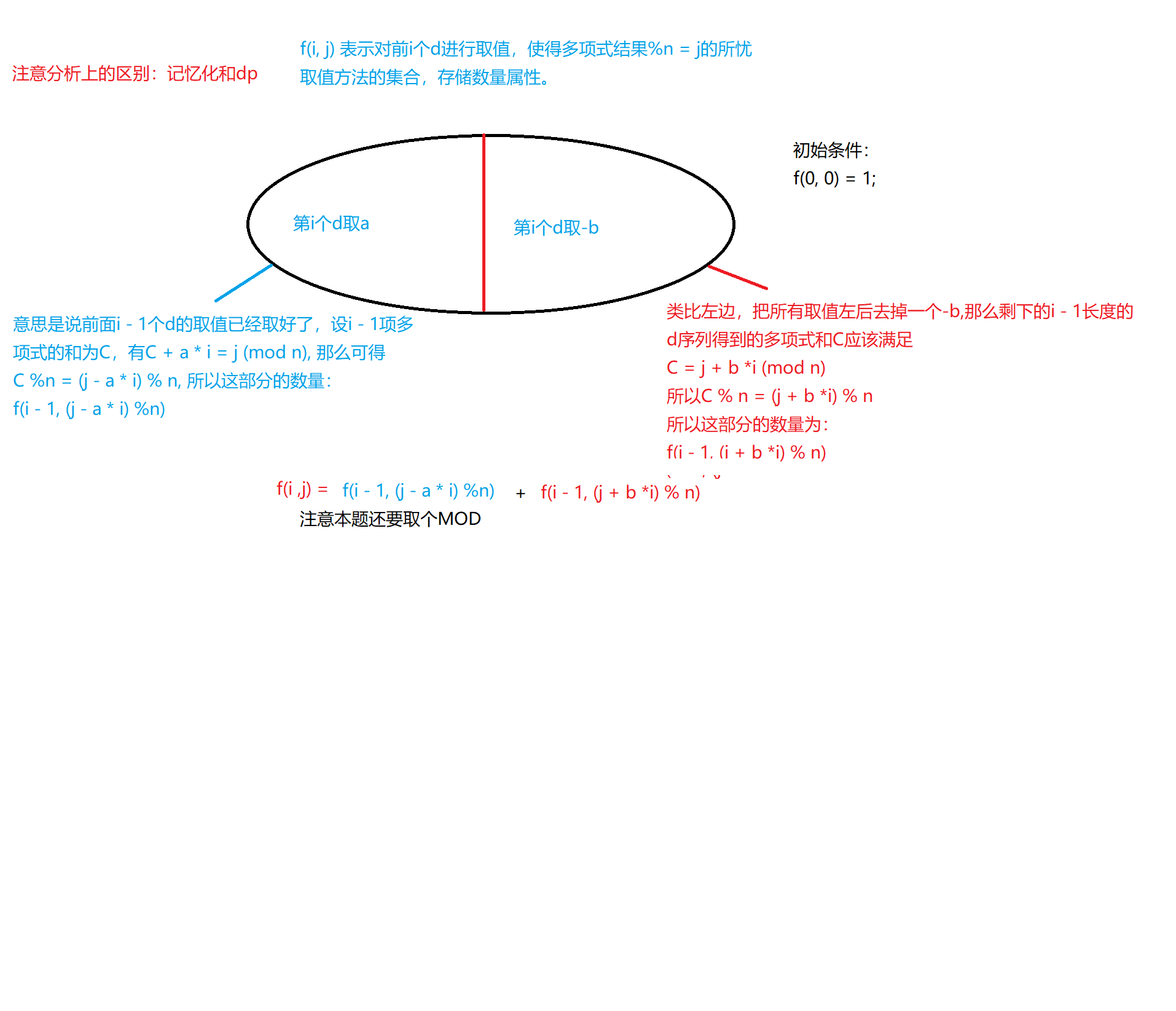
记忆化分析：

dp代码

#include<iostream>
#include<cstring>

using namespace std;

const int N = 1010, MOD = 100000007;

int f[N][N];
int n, s, a, b;

int get_mod(int a, int b){
    return (a % b + b) % b;
}

int main(){
    cin >> n >> s >> a >> b;
    
    f[0][0] = 1;
    
    for(int i = 1; i < n; i ++)
        for(int j = 0; j < n; j ++)
            f[i][j] = (f[i - 1][get_mod(j - a * i, n)] + f[i - 1][get_mod(j + b * i, n)]) % MOD;
    
    cout << f[n - 1][get_mod(s, n)] << endl;
    
    return 0;
}

记忆化代码

#include<iostream>
#include<cstring>

using namespace std;

const int N = 1010, MOD = 100000007;

int f[N][N], st[N][N];
int n, s, a, b;

int get_mod(int a, int b){
    return (a % b + b) % b;
}

int dfs(int i, int j){
    if(i == 0 && j == 0) st[i][j] = f[i][j] = 1;
    if(!st[i][j]){
        st[i][j] = 1;
        if(i)
            f[i][j] = (dfs(i - 1, get_mod(j - a * (n - i), n)) + dfs(i - 1, get_mod(j + b * (n - i), n))) % MOD;
    }
    return f[i][j];
}

int main(){
    cin >> n >> s >> a >> b;
    
    memset(f, 0, sizeof f);
    cout << dfs(n - 1, get_mod(s, n));
    
    return 0;
}