二分图匹配之匈牙利算法
二分图的基本概念:
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
比如:
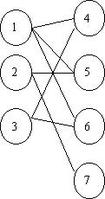
我们一般把图的两部分称为X部和Y部,一个图的所有点如果能被两个独立的点集,那就认为这个图是二分图
二分图的判断一般通过染色的方法来进行判段,可以写成dfs或则bfs的写法
bool dfs(int v,int c) { color[v]=c; for(int i=0;i<n;i++) { if(edge[v][i]==1) { if(color[i]==c) return false; if(color[i]==0&&!dfs(i,-c)) return false; } } return true; } void solve() { int flag=0; for(int i=0;i<n;i++) { if(color[i]==0) { if(!dfs(i,1)) { cout<<"no"<<endl; flag=1; break; } } } if(!flag) cout<<"yes"<<endl; }
bfs写法
bool bfs(int s) { color[s] = 1; queue<int> que; que.push(s); while(!que.empty()) { int from = que.front(); que.pop(); for(int i = 1; i <= V; i++) { // 如果相邻的点没有上色就给这个点上色 if(G[from][i] && color[i] == 0) { que.push(i); color[i] = -color[from]; } // 如果相邻的颜色相同则返回false if(G[from][i] && color[i] == color[from]) return false; } } // 如果所有的点都被染过色,且相邻的点颜色都不一样,返回true return true; }
接下来就是介绍匹配:
一个匹配是一个边的集合,任何匹配的边之间没有公共顶点。
最大匹配:一个图的所有匹配中,边数最多的匹配称为最大匹配。如果所有定点都是匹配顶点,则称这个匹配为完美匹配。
我们一般通过匈牙利算法来求一个二分图的最大匹配,其算法的核心是求增广路径。
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。*
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。
我们每次找到一个增广路,所得到的匹配的边数都会增加一条,因此我们可以通过求所有点的增广路径来求最大匹配的边数
匈牙利算法的模板如下:
bool dfs(int x) { for(int i=1;i<=p;i++) { if(!used[i]&&map[x][i]==1) { used[i]=1; if(!link[i]||dfs(link[i])) { link[i]=x; return true; } } } return false; } void xyl() { for(int i=1;i<=n;i++) { memset(used,0,sizeof(used)); if(dfs(i)) counts++; } }
PS.练习题:hdu 1045,hdu 2444,hdu 1083
此外还有二分图的最小顶点覆盖,最大独立集,最大团等知识,求的方法和匈牙利算法的差不多可以参考如下博客
https://www.cnblogs.com/jianglangcaijin/p/6035945.html
剩下的带权二分图过几天在补充


