C++数据结构和算法:位运算、字符串
--------------------------------位运算---------------------------------
Q1. 用位运算交换两个值
前提:要交换的两个值是独立内存
void Swap(int& a, int& b) { a = a ^ b; b = a ^ b; a = a ^ b; }
Q2. 有一个数组,有些数字出现次数为偶数,只有一个数字出现次数为奇数,请在O(N)内找到这个数
解析:假设数组为 { 2,1,3,1,2,1,3 } ,∵ N^N=0,N^0=N,∴ 0^2^1^3^1^2^1^3 = 2^1^3^1^2^1^3 = 0^1^3^1^1^3 = 0^1^1^1^0 = 0^1^1^1 = 0^0^1 = 0^1 = 1
偶数次的一定会累计异或为0,奇数次的一定会累计异或为本身,所以只要用0去累计异或所有数就行了,最后得到的就是这个奇数次数。
1 void PrintOddTimesNum(int arr[],int len) 2 { 3 int eor = 0; 4 for (int i=0;i<len;i++) 5 { 6 eor ^= arr[i]; 7 } 8 cout << eor << endl; 9 }
Q4. 上一题条件改为出现奇数次的数字有两个,要找出这两个数
解析:如果按上一题方法,0跟所有数异或之后得到的是 a^b,那么怎么分离a和b呢?
∵ 异或运算偶数次的数会抵消为0,奇数次的数会抵消为本身
∴ 所有数累计异或,一定会得到奇数次的数之间异或,eor=a^b
∵ a≠b,异或运算相同位为0,不同位为1
∴ eor至少有一位为1,而且这一位,在a中为1,在b中为0,那么就可以把数组分为,这1位为1的数和这一位为0的数。
假设我们先找这一位为1的数,全部累计异或,偶数次的数会抵消为0,奇数次的数会抵消为本身,所以最后会得到这一位为1且奇数次的数;
先找这一位为0的数道理一样。
假设找到的这个数是a ,∵ eor = a^b
∴ eor^a = a^b^a = 0^b = b,用a异或eor就能得到b。
1 void PrintOddTimesNum(int arr[],int len) 2 { 3 int eor = 0; 4 for (int i=0;i<len;i++) 5 { 6 eor ^= arr[i]; 7 } //EOR = a^b 8 9 //找最右1 10 //一个数&自己的补码得到最右1 11 //补码 = 取反进1 12 int rightOne = eor & (~eor + 1); 13 14 int a=0; 15 for (int i=0;i<len;i++) 16 { 17 if ((arr[i] & rightOne) == rightOne) //也可以是==0来判断 18 a ^= arr[i]; 19 } 20 21 cout << "a=" << a << " b=" << (a ^ eor) << endl; 22 }
--------------------------------字符串---------------------------------
—— KMP 字符串匹配算法 ——
核心:利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
时间复杂度:O(m+n)
第一步:构造next数组
法则:值=公共前后缀的长度
eg. abaa
| 下标 | 比较元素 | 前缀 | 后缀 | 值 |
| 0 | a | {} | {} | 0 |
| 1 | ab | a | b | 0 |
| 2 | aba | a、ab | a、ba | 1 |
| 3 | abaa | a、ab、aba | a、aa、baa | 1 |
第二步:匹配
比较到后缀不匹配位置,把模式串前缀移动到原来的后缀位置;
1 //计算next数组 2 int arr_next[1000]; 3 void BuildNext(const string pattern) 4 { 5 arr_next[0] = 0; // 第一个字符的最长相同前缀后缀为0 6 for (int i = 1, j = 0; i < pattern.length(); i++) 7 { 8 while (j && pattern[i] != pattern[j]) 9 { 10 j = arr_next[j - 1];//如果不相同,移动p,这里如果j=0并且两个字符还不相同,也就默认pmt[i] = 0了 11 } 12 13 if (pattern[i] == pattern[j]) 14 { 15 j++; 16 arr_next[i] = j;//如果相同,则得到该位置pmt[i]的值,继续向后比较 17 } 18 } 19 for (int i = 0; i < pattern.length(); i++) 20 cout << arr_next[i] << " "; 21 cout << endl; 22 } 23 24 int KMP(const string str, const string pattern) 25 { 26 for (int i = 0, j = 0; i < str.length(); i++) 27 { 28 while (j && str[i] != pattern[j]) j = arr_next[j - 1]; 29 if (str[i] == pattern[j]) 30 { 31 j++; // 两者相等,继续匹配 32 } 33 if (j == pattern.length()) 34 { 35 return i - j + 1;//匹配成功,返回下标 36 37 } 38 } 39 return -1;// 未匹配成功,返回-1 40 }
—— 键索引计数法 字符串排序算法 ——
假设要给不同班级的学生按班级排序
1 struct student 2 { 3 int stuClass; 4 string stuName; 5 }; 6 vector<student> students = { {2,"Anderson"},{3,"Brown"},{3,"Davis"},{4,"Garcia"},{1,"Harris"},{3,"Jackson"},{4,"Johnson"},{3,"Jones"},{1,"Martin"},{2,"Martinez"},{2,"Miller"},{1,"Moore"},{2,"Robinson"},{4,"Smith"}, 7 {3,"Taylor"},{4,"Thomas"},{4,"Thompson"},{2,"White"},{3,"Williams"},{4,"Wilson"} };
准备一个用于接收排序后数据的容器
vector<student> aux = students;
排序规模N,索引数组大小R
const int N = students.size();
const int R = 5; //班级数量+1
索引数组
int count[R+1] = { 0 }; //+1防止溢出,用于存储计算结果
===> 计算班级出现的频率
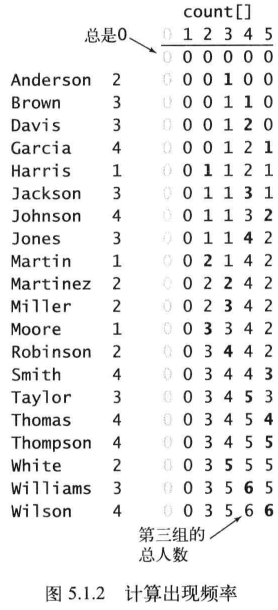
for (int i = 0; i < N; i++)
count[students[i].stuClass]++;
===> 将频率转化为索引 count[i] 表示 ≤ i 的总数
| 0 | 1 | 2 | 3 | 4 |
| 0 | 3 | 5 | 6 | 6 |
| 3 | 5 | 6 | 6 | |
| 8 | 6 | 6 | ||
| 14 | 6 | |||
| 20 |
for (int r = 0; r < R; r++)
count[r + 1] += count[r];
===> 将学生按班级分类
拆解
aux[count[students[i].stuClass - 1]++].stuClass = students[i].stuClass;
students[i].stuClass 代表 第 i 个学生所在班级
count[students[i].stuClass] 代表 小于等于 所在班级的人数
count[students[i].stuClass - 1] 代表 小于所在班级的人数
aux[count[students[i].stuClass - 1]++] 把当前学生放在 小于所在班级的人数 后面一个,再++ 表示小于所在班级的人数+1,这样下次遇到同一班级就在这个学生后面1位了
for (int i = 0; i < N; i++)
{
aux[count[students[i].stuClass - 1]].stuName = students[i].stuName;
aux[count[students[i].stuClass - 1]++].stuClass = students[i].stuClass;
}
===> 输出排序后结果
for (int i = 0; i < N; i++)
{
cout << "class: "<<aux[i].stuClass<<" name: "<<aux[i].stuName<< endl;
}
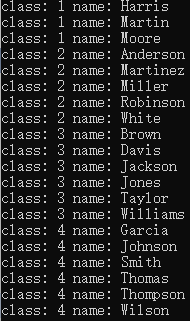
举一反三:替换比较对象,可以实现按指定位排序
其他算法参考:https://www.cnblogs.com/mcomco/p/10366184.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号