手柄陀螺仪、加速度计算

一、基本概念

陀螺仪可选量程：± 15.6/31.2/62.5/125/250/500/1000/2000 dps

加速度可选量程：± 2/4/8/16 g

 

 

 计算单位：

 

　　陀螺仪：角速度=速度*时间。单位：dps 度每秒。

　　加速度计：静止状态，重力加速度=1g≈9.8 米/平方秒。

表示：

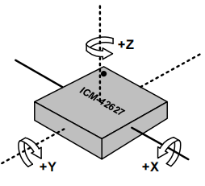
　　gx  gy  gz  代表陀螺仪在x,y,z轴上的分量

　　ax  ay  az  代表加速度计在x,y,z轴上的分量

传感器包含三轴加速度计和三轴陀螺仪数据，每个轴用 2 KB表示，例如加速度x轴：

　　A_XSENSOR&0XFF　　取低八位

　　A_XSENSOR>>8　　　  取高八位

坐标轴：以笛卡尔右手坐标系为准

横滚角 Roll：飞机右滚为正。绕z轴旋转。

俯仰角 Pitch：飞机抬头为正。绕x轴旋转。

偏航角 Yaw：实际航向与计划航向之间的夹角，向右偏为正。绕y轴旋转。

 

 

二、传感器重要参数及物理量换算

陀螺仪和加速度的量程：以 2000 dps 和 16 g 为例 

量程对应的精度：以 16.4 LSB 和 2048 LSB 为例

寄存器数据16位，最高位符号位，输出范围为-7FFF~7FFF，即-32767到32767

四轴姿态计算中，陀螺仪数据计算公式：

　　　　gyro_x / (16.40 * 1弧度) = gyro_x / (16.40 * 57.30) = gyro_x * 0.001064

加速度计算公式：

　　　　32737对应16g，32767/16≈2048，即灵敏度。

　　　　 accel_x/2048 g ,1g=9.8 m²/s

物理量换算如下：

三、噪声滤波

互补滤波

 

Kalman滤波

数据融合滤波

 

四、姿态解算

姿态解算最小依赖：惯性传感器数据

只用加速度做姿态解算

 

横滚角φ=arctan(Ay/Az)，代表重力加速度与X-Z平面的夹角

==>在三维空间，公式为：φ=arctan(Ay/sqrt(Ax²+Az²))

 

 

俯仰角：θ=arctan(-Ax/sqrt(Ay²+Az²))

 

 

只用陀螺仪做姿态解算

陀螺仪输出到姿态角速度的转换矩阵=[1, sin(phi)*tan(theta), cos(phi)*tan(theta);

                                                             0,         cos(phi),             -sin(phi);

                                                             0,  sin(phi)*sec(theta), cos(phi)*sec(theta)];

平台：matlab，其中phi表示重力加速度与X-Z平面夹角，theta表示重力加速度与Y-Z平面夹角。

陀螺仪各轴输出为：gyro = [gx gy gz]' ;

姿态角速度算法：[横滚角速度，俯仰角速度，偏航角速度]' = trans * gryo;

姿态角（循环里累计角度变化）：attitude_gyro = attitude_gyro + trans * gyro .* dt ;