数据结构
数组
数组简介
数组定义
数组是一种线性数据结构,它使用一组连续的内存空间,存储一组相同类型的数据。
数组是实现线性表的顺序结构存储的基础。
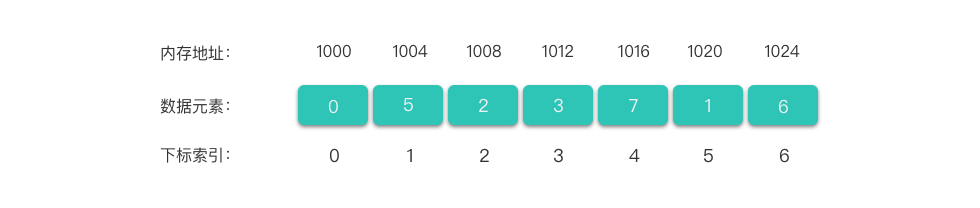
如上图所示,数组的每一个数据都有它自己的下标索引。一个长度为 n 的数组,索引下标从 0 开始到 n-1 结束。每一个下标索引都对应着数组中的一个数据。
因为数组使用的是一组连续的内存空间,每个数据之间都有自己的内存空间,并且元素之间是紧密排列的。每个数据之间的间隔是对应数据类型所占内存空间大小,如 int 类型的数据在64位系统中占内存空间 4个字节 所以int类型的数据在数组中每个数据的间隔是4个字节大小。
- 线性表:线性表就是所有数据元素排成像一条线一样的结构,线性表上的数据元素都是相同类型,且每个数据元素最多只有前、后两个方向。数组就是一种线性表结构。此外,栈、队列、链表都是线性表结构。
- 连续的内存空间:线性表有两种存储结构:「顺序存储结构」和「链式存储结构」。其中,「顺序存储结构」是指占用的内存空间是连续的,相邻数据元素之间,物理内存上的存储位置也相邻。数组也是采用了顺序存储结构,并且存储的数据都是相同类型的。
随机访问数据元素
数组的最大特点就是能够随机访问元素数据,数组可以根据下标,直接定位到元素存放的位置。
计算机给一个数组分配了一组连续的存储空间,其中第一个元素开始的地址被称为 「首地址」。每个数据元素都有对应的下标索引和内存地址,计算机通过地址来访问数据元素。当计算机需要访问数组的某个元素时,会通过 「寻址公式」 计算出对应元素的内存地址,然后访问地址对应的数据元素。
寻址公式如下:下标 𝑖*i* 对应的数据元素地址 = 数据首地址 + 𝑖*i* × 单个数据元素所占内存大小。
多维数组
一维数组不能够满足我们存储数据要求,因为在现实中数据是多维的。例如一个人,人拥有姓名,年龄,身高,体重等等。所以使用一维数组并不能满足存储数据的需求。
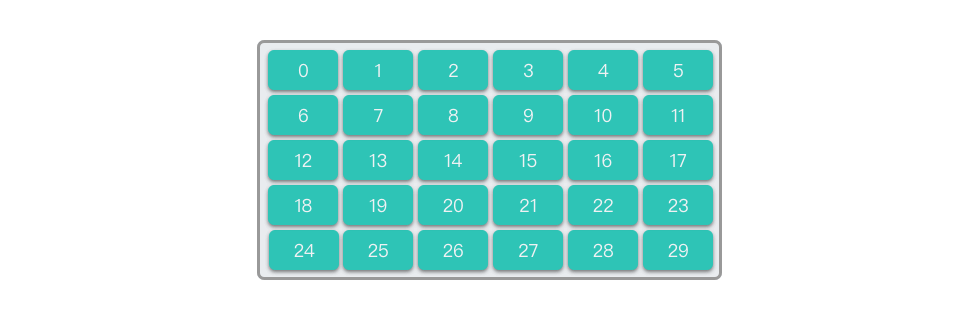
二维数组是由m行和n列数据元素组成的特殊结构,本质上是将一个个一维数组组成二维数组的元素,每一个元素就是一个数组。也可以叫做「数组的数组」。
数组的实现
在c/c++中数组内存储的数据在内存空间中都是连续存储的。
- 一维数组初始化:
// 初始化一个包含 5 个整数的数组
int arr[5] = {1, 2, 3, 4, 5};
// 也可以部分初始化,未初始化的元素将默认为 0
int arr[5] = {1, 2}; // 结果是 {1, 2, 0, 0, 0}
// 还可以省略数组大小,由初始化列表的长度决定数组大小
int arr[] = {1, 2, 3, 4, 5};
- 二维数组的初始化
// 声明一个 3x3 的二维数组
int arr[3][3];
// 初始化一个 2x3 的二维数组
int arr[2][3] = {
{1, 2, 3},
{4, 5, 6}
};
// 部分初始化,一个 3x3 的二维数组
int arr[3][3] = {
{1, 2}, // 初始化第一行,未指定的元素默认为 0
{4, 5, 6} // 初始化第二行
// 第三行默认初始化为 0
};
数组基本操作
数据结构的操作一般涉及增,删,查,改四种情况。
访问元素
访问数组中第 i个元素:
- 只需要检查 i 的范围是否在合法的范围区间,即
0≤𝑖≤𝑙𝑒𝑛(𝑛𝑢𝑚𝑠)−1。超出范围的访问为非法访问。 - 当位置合法时,由给定下标得到元素的值。
int arr[5] = {1, 2, 3, 4, 5};
//遍历访问数组中的数据
for(int i=0;i<5;i++)
{
printf("%d ",arr[i]);
}
输出:1 2 3 4 5
「访问数组元素」的操作不依赖于数组中元素个数,因此,「访问数组元素」的时间复杂度为 𝑂(1)。
查找元素
查找数组中的元素时,需要注意查找的范围必须在数组的大小范围[0 , (n-1)] 闭区间,n为数组的长度大小。
int findValue(int *arr, int val, int size)
{
for (int i = 0; i < size; i++)
{
if (arr[i] == val)
{
return i;//如果找到,则返回该元素的下标
}
}
return -1; // 如果找不到值,则返回 -1
}
int main()
{
int arr[5] = {1, 2, 3, 4, 5};
int size = sizeof(arr) / sizeof(int);
int *p = arr;
findValue(p, 2, size);
return 0;
}
上述代码 ,通过 findValue 函数实现查找数组元素,成功返回元素下标,失败返回-1。
在「查找元素」的操作中,如果数组无序,那么我们只能通过将 val 与数组中的数据元素逐一对比的方式进行查找,也称为线性查找。而线性查找操作依赖于数组中元素个数,因此,「查找元素」的时间复杂度为 𝑂(𝑛)。
插入元素
插入元素操作分为两种:「在数组尾部插入值为 val 的元素」和「在数组第 i个位置上插入值为 val的元素」。
在数组尾部插入值为 val 的元素:
- 如果数组尾部容量不满,则直接把
val放在数组尾部的空闲位置,并更新数组的元素计数值。 - 如果数组容量满了,则插入失败。不过,Python 中的 list 列表做了其他处理,当数组容量满了,则会开辟新的空间进行插入。
在数组第 i 个位置上插入值为 val 的元素:
- 先检查插入下标 i 是否合法,即
0≤𝑖≤𝑙𝑒𝑛(𝑛𝑢𝑚𝑠)。 - 确定合法位置后,通常情况下第 i 个位置上已经有数据了(除非
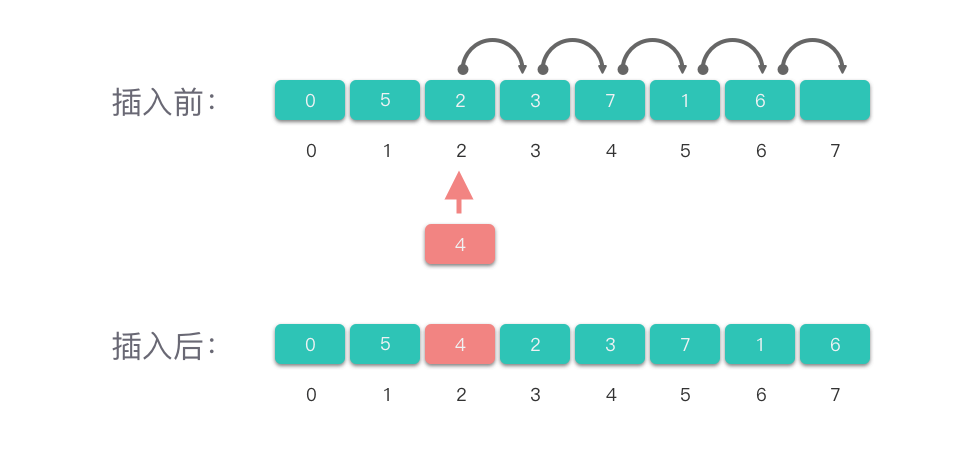
𝑖==𝑙𝑒𝑛(𝑛𝑢𝑚𝑠),要把第𝑖∼𝑙𝑒𝑛(𝑛𝑢𝑚𝑠)−1位置上的元素依次向后移动。 - 然后再在第 i 个元素位置赋值为 val,并更新数组的元素计数值。
void insertElement(int arr[], int *size, int element, int position)
{
// 检查位置是否有效
if (position < 0 || position > *size)
{
printf("Invalid position to insert.\n");
return;
}
// 移动元素,为新元素腾出位置
for (int i = *size; i > position; i--)
{
arr[i] = arr[i - 1];
}
// 插入新元素到指定位置
arr[position] = element;
// 数组大小增加
(*size)++;
}
int main()
{
int arr[7] = {0, 5, 2, 3, 7, 1, 6}; // 初始化一个包含7个元素的数组
int size = 7; // 数组的当前大小
int element = 4; // 要插入的元素
int position = 2; // 要插入的位置(从0开始)
// 调用插入函数
insertElement(arr, &size, element, position);
}
上述 insertElement 实现了在数组中插入元素的操作。
「在数组中间位置插入元素」的操作中,由于移动元素的操作次数跟元素个数有关,因此,「在数组中间位置插入元素」的最坏和平均时间复杂度都是 𝑂(𝑛)。
改变元素
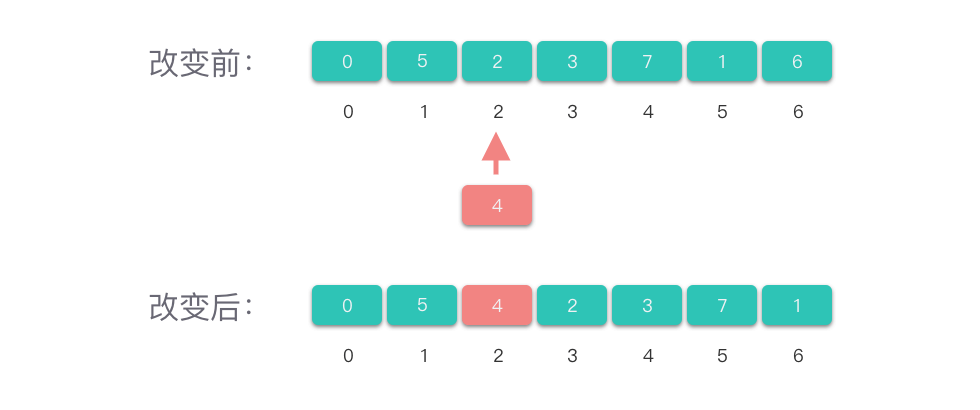
将数组中第 i 个元素值改为 val:
- 需要先检查 i 的范围是否在合法的范围区间,即
0≤𝑖≤𝑙𝑒𝑛(𝑛𝑢𝑚𝑠)−1。 - 然后将第 i 个元素值赋值为 val。
#include <stdio.h>
// 修改数组元素的函数
void changeElement(int arr[], int index, int newValue)
{
arr[index] = newValue;
}
// 主函数
int main()
{
int arr[7] = {0, 5, 2, 3, 7, 1, 6}; // 初始化一个包含7个元素的数组
// 修改数组的第3个元素(索引为2)为值为4
changeElement(arr, 2, 4);
return 0;
}
「改变元素」的操作跟访问元素操作类似,访问操作不依赖于数组中元素个数,因此,「改变元素」的时间复杂度为 𝑂(1)。
删除元素
删除元素分为三种情况:「删除数组尾部元素」、「删除数组第 i 个位置上的元素」、「基于条件删除元素」。
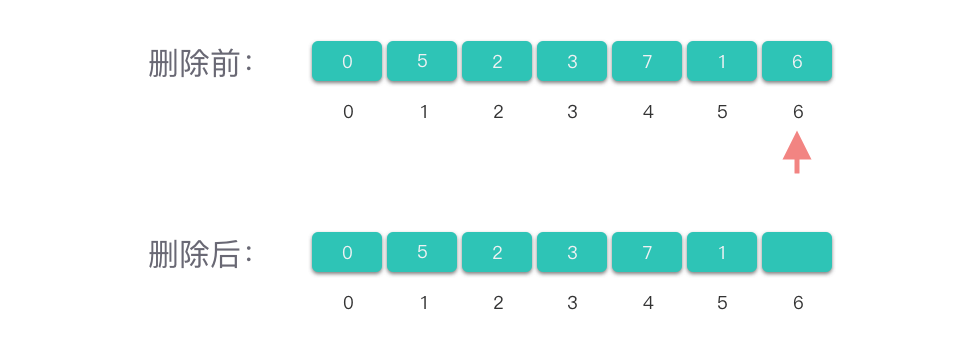
删除数组尾部元素:
- 只需将元素计数值减一即可。
// 删除数组尾部元素的函数
void deleteTail(int arr[], int *size)
{
if (*size <= 0)
{
printf("Array is already empty.\n");
return;
}
// 减少数组的大小(相当于删除最后一个元素)
(*size)--;
}
「删除数组尾部元素」的操作,不依赖于数组中的元素个数,因此,「删除数组尾部元素」的时间复杂度为 𝑂(1)。
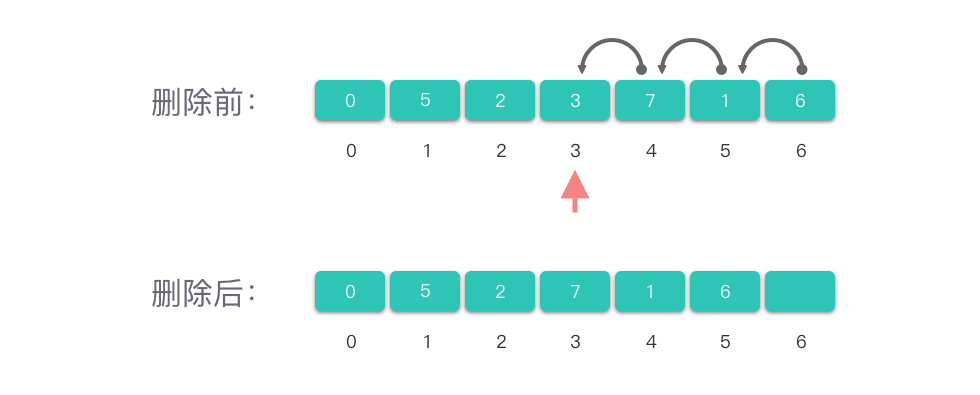
删除数组第 𝑖*i* 个位置上的元素:
- 先检查下标 **i **是否合法,即
0≤𝑖≤𝑙𝑒𝑛(𝑛𝑢𝑚𝑠)−1。 - 如果下标合法,则将第
𝑖+1个位置到第𝑙𝑒𝑛(𝑛𝑢𝑚𝑠)−1位置上的元素依次向左移动。 - 删除后修改数组的元素计数值。
#include <stdio.h>
// 删除数组元素的函数
void deleteElement(int arr[], int *size, int position)
{
// 检查位置是否有效
if (position < 0 || position >= *size)
{
printf("Invalid position to delete.\n");
return;
}
// 将后续元素向前移动
for (int i = position; i < *size - 1; i++)
{
arr[i] = arr[i + 1];
}
// 减少数组的大小
(*size)--;
}
// 主函数
int main()
{
int arr[5] = {1, 2, 3, 4, 5}; // 初始化一个包含5个元素的数组
int size = 5; // 数组的当前大小
// 删除数组的第3个元素(索引为2)
deleteElement(arr, &size, 2);
return 0;
}
「删除数组中间位置元素」的操作同样涉及移动元素,而移动元素的操作次数跟元素个数有关,因此,「删除数组中间位置元素」的最坏和平均时间复杂度都是 𝑂(𝑛)。
总结
数组是最基础、最简单的数据结构。数组是实现线性表的顺序结构存储的基础。它使用一组连续的内存空间,来存储一组具有相同类型的数据。
数组的最大特点的支持随机访问。访问数组元素、改变数组元素的时间复杂度为 𝑂(1),在数组尾部插入、删除元素的时间复杂度也是 𝑂(1),普通情况下插入、删除元素的时间复杂度为 𝑂(𝑛)。
所以数组比较适合数据量固定,频繁查询,较少增,删的场景。
数组排序
冒泡排序
冒泡排序,顾名思义:排序的过程就像是旗袍在水底向上冒出
过程:
想象一组数据,元素和气泡的大小成正比。
- 将第一个位置的气泡和后面的气泡相比较:
- 如果当前气泡比后面的气泡大,则交换这两个气泡的位置。
- 如果前面的气泡比后面的气泡小,位置不变。
- 将需要判断的位置向后移动一位,这个时候来到了第二个气泡的位置,重复第一步,直到这个位置到最后一个气泡,那么结束排序。
- 在排序完成之后,最大的气泡会在这个集合的最右边,最小的气泡则在最左边,达到冒泡排序的效果。
过程如图:

具体的步骤如下:
- 初始化:定义一个临时变量
temp用于交换数组元素。 - 外层循环:遍历数组,从第一个元素开始,控制需要进行多少次排序操作,循环次数为
len - 1次。 - 内层循环:每次遍历数组中相邻的两个元素,进行比较和交换,比较次数为
len - 1 - i次,i是外层循环的变量。 - 比较和交换:如果当前元素
arr[j]大于相邻的下一个元素arr[j + 1],则交换它们的位置。
void my_sort(int *arr, int len)
{
// 冒泡排序
int temp;
for (int i = 0; i < len - 1; i++)
{
for (int j = 0; j < len - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
// 判断如果当前元素与
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
选择排序
选择排序(Selection Sort)是一种简单的排序算法,它的工作原理是反复从待排序的数据元素中选择最小(或最大)的一个元素,将其放到已排序的序列的末尾。
算法步骤:
第一步:所有未经过排序的数据元素中选择第一个未排序的元素,将选中的元素设置为最小值【MIN】。
第二步:选中元素与未排序的元素进行比较,如果有小于当前最小值的元素,将这个元素赋值为最小值【MIN】,直到比较所有未排序集合中的元素。
第三步:然后将最小值和未排序集合的第一位进行交换位置。
第四步:现在未排序的数据集合长度减一,继续从未排序的数据集合中选择第一个未排序的元素,以此类推。直到未排序的元素只有一个为止,完成选择排序。
如下图所示:
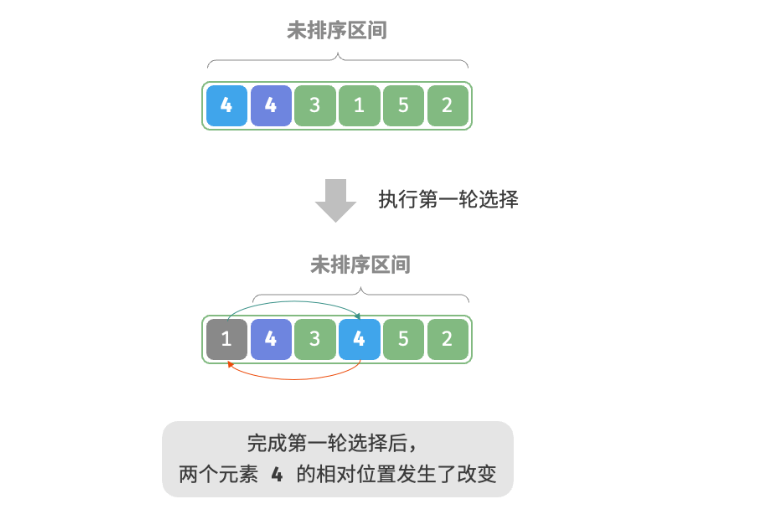
具体步骤:
- 初始化:定义一个临时变量
min_index用于记录每次查找中的最小元素索引。 - 外层循环:遍历数组,从第一个元素开始,控制需要进行多少次排序操作,循环次数为
len - 1次。 - 内层循环:在每次外层循环中,从
i位置开始遍历数组的剩余部分,找到未排序部分中的最小元素,比较次数为len - i - 1次,i是外层循环的变量。 - 找最小值和交换:在每次内层循环结束后,如果找到的最小元素
arr[min_index]不是当前i位置的元素,则将它与i位置的元素交换。
void selection_sort(int *arr, int len) {
for (int i = 0; i < len - 1; i++) {
int min_index = i; // 假设当前索引是最小值
for (int j = i + 1; j < len; j++) {
if (arr[j] < arr[min_index]) {
min_index = j; // 找到未排序部分的最小值索引
}
}
// 交换找到的最小元素与当前位置的元素
if (min_index != i) {
int temp = arr[min_index];
arr[min_index] = arr[i];
arr[i] = temp;
}
}
}
插入排序
插入排序算法步骤
- 从第一个元素开始,该元素可以认为已经被排序。
- 取出下一个元素,在已经排序的元素序列中从后向前扫描。
- 如果被扫描的元素(已排序)大于新元素,将该元素后移一位。
- 重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置。
- 将新元素插入到该位置后。
- 重复步骤 2~5。
如下图所示:
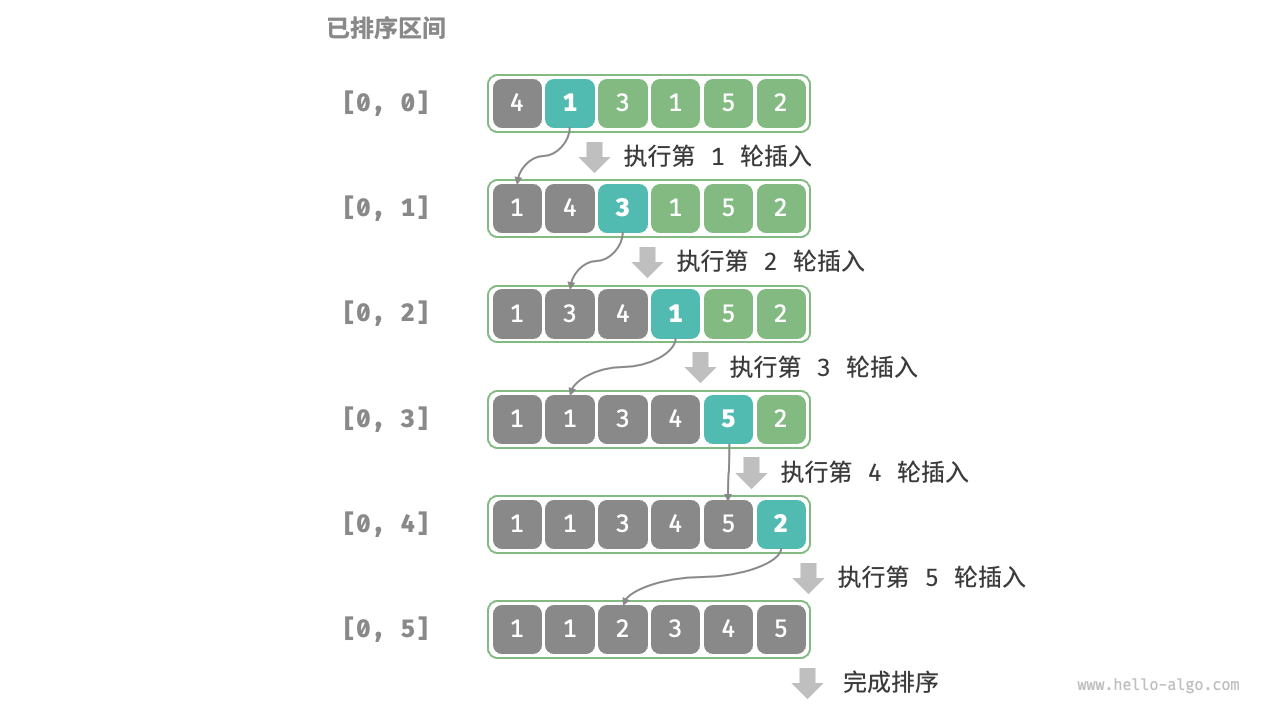
具体步骤:
- 首先将需要插入的元素赋值给base,判断已排序区间内是否有大于base的值,如果有则将已排序区间的数据向后移动一位。
- 然后将base插入合适的位置,完成第一次排序。
- 以此类推,直到遍历完整个数组。
// 插入排序
void insertionSort(int *arr, int size)
{
for (int i = 1; i < size; i++)
{
// 默认数组第一位数据为以排序数据
// 将需要插入的元素赋值给base,令j追踪已排序区间的最后一位
int base = arr[i], j = i - 1;
while (j >= 0 && arr[j] > base)
{
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = base;
}
}
外循环for实现:
- 外循环从索引
1开始到数组的末尾。 base用于存储当前要插入的元素,即nums[i]。j用于追踪已排序区间的最后一个元素,即i-1。
内循环while实现:
- 内循环条件为
j >= 0且nums[j] > base,即在已排序区间中,从右向左查找比base大的元素。 - 如果
nums[j] > base,将nums[j]向右移动一位,即nums[j + 1] = nums[j],并将j减1。 - 这一步会不断将已排序区间中大于
base的元素向右移动,直到找到一个不大于base的元素或者到达数组的开头。
插入元素:
- 当内循环结束时,
j已经移动到了比base小的元素的索引位置(或者 -1)。 - 这时将
base插入到nums[j + 1]位置,即将当前元素插入到已排序区间的正确位置。



