2.6 树和二叉树

树是什么

​ 线性结构中，一个节点至多只有一个头节点，至多只有一个尾节点，彼此连接起来是一条完整的线。

比如链表和数组;

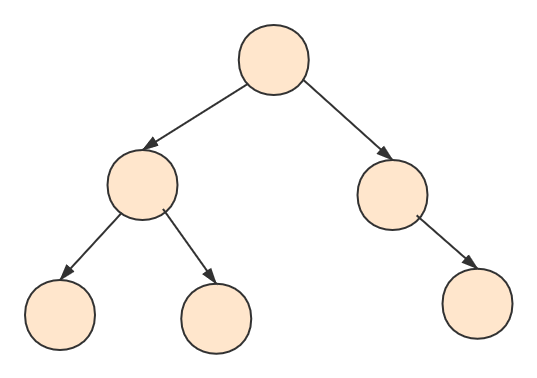
​ 而树，非线性结构的典型例子，不再是一对一，而变成了一对多（而图则可以是 多对多），树如下图所示：

基本概念

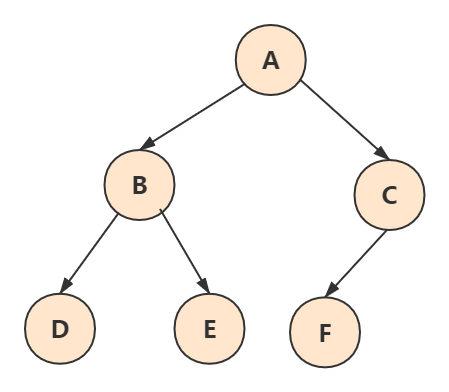
如下图：

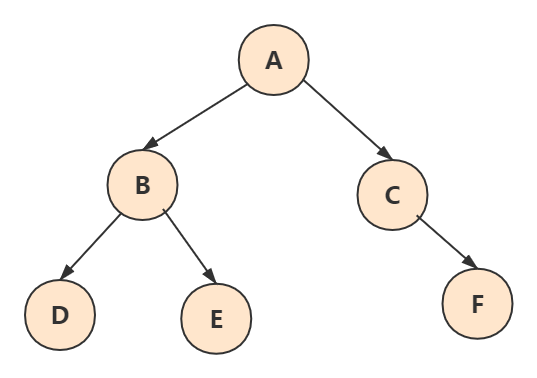
• 根节点 ：A
• 父节点 ： A是B、C的父节点；B是D、E的父节点；C是F的父节点
• 兄弟节点 ： B、C互为兄弟节点（有共同的父节点A）；DE互为兄弟节点（有共同的父节点B）；F没有兄弟节点
• 子节点（孩子）：B、C是A的子节点；D、E是B的子节点；F是C的子节点
• 叶子节点：D、E、F没有子节点，所以它们是叶子节点
• 层 ： A是第一层 ； B、C是第二层； D、E、F是第三层
• 深度（高度）：最大层数就是深度，所以深度为 3

二叉树

二叉树中，每个结点最多有两个分支，即每个结点最多有两个子结点，分别称作左子结点和右子结点。

满二叉树

定义为除了叶子结点外，所有结点都有 2 个子结点。如下图：

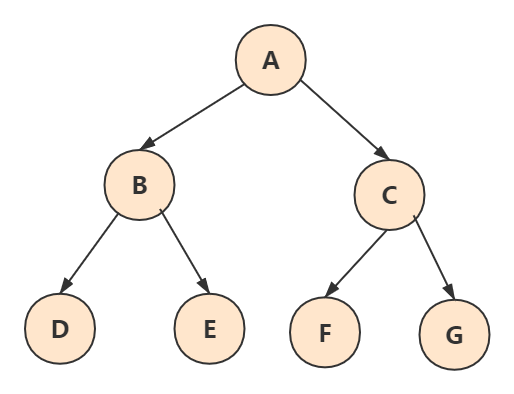
完全二叉树

定义为除了最后一层以外，其他层的结点个数都达到最大，并且最后一层的叶子结点都靠左排列。如下图：

树的基本操作

• 前序遍历：对树中的任意结点来说，先打印这个结点，然后前序遍历它的左子树，最后前序遍历它的右子树。
• 中序遍历，对树中的任意结点来说，先中序遍历它的左子树，然后打印这个结点，最后中序遍历它的右子树。
• 后序遍历，对树中的任意结点来说，先后序遍历它的左子树，然后后序遍历它的右子树，最后打印它本身。

二叉查找树（二叉搜索树）

• 在二叉查找树中的任意一个结点，其左子树中的每个结点的值，都要小于这个结点的值。
• 在二叉查找树中的任意一个结点，其右子树中每个结点的值，都要大于这个结点的值。
• 在二叉查找树中，会尽可能规避两个结点数值相等的情况。
• 对二叉查找树进行中序遍历，就可以输出一个从小到大的有序数据队列。

例题

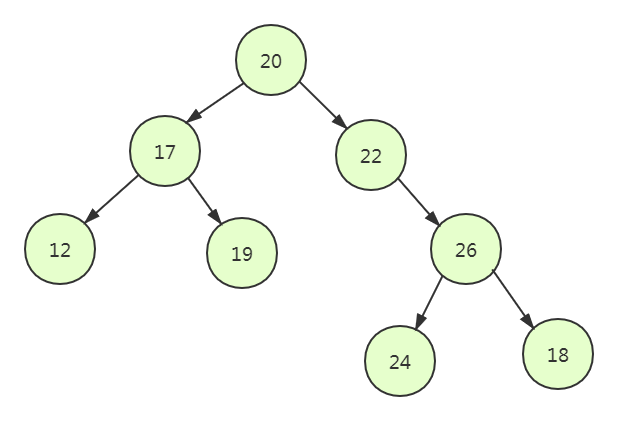
给定一棵树，按照层次顺序遍历并打印这棵树。例如:

则打印 20、17、22、12、19、26、24、18。请注意，这并不是前序遍历

解：

import java.util.LinkedList;

public class TreeTest {

	public static void main(String[] args) {

		Node<Integer> node = new Node<Integer>(20,
				new Node<Integer>(17, new Node<Integer>(12, null, null), new Node<Integer>(19, null, null)),
				new Node<Integer>(22, null,
						new Node<Integer>(26, new Node<Integer>(24, null, null), new Node<Integer>(18, null, null))));

		//
		levelTraverse(node);
	}

	/**
	 * 核心思路 队列
	 * 
	 * -->入队的顺序 是从第一层开始，由左至右进行
	 * 
	 * @param root
	 */
	public static void levelTraverse(Node root) {

		if (root == null) {

			return;

		}

		LinkedList<Node> queue = new LinkedList<Node>();

		Node current = null;

		queue.offer(root); // 根节点入队

		while (!queue.isEmpty()) { // 只要队列中有元素，就可以一直执行，非常巧妙地利用了队列的特性

			current = queue.poll(); // 出队队头元素

			System.out.print(" " + current.data);

			// 左子树不为空，入队

			if (current.left != null)

				queue.offer(current.left);

			// 右子树不为空，入队

			if (current.right != null)

				queue.offer(current.right);

		}

	}

	static class Node<T> {
		T data;
		Node left;
		Node right;

		public Node() {
		}

		public Node(T data, Node left, Node right) {
			this.data = data;
			this.left = left;
			this.right = right;
		}

		public T getData() {
			return data;
		}

		public void setData(T data) {
			this.data = data;
		}

		public Node getLeft() {
			return left;
		}

		public void setLeft(Node left) {
			this.left = left;
		}

		public Node getRight() {
			return right;
		}

		public void setRight(Node right) {
			this.right = right;
		}

	}
}