hdu Interesting Fibonacci
Interesting Fibonacci
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 665 Accepted Submission(s): 114
Problem Description
In mathematics, the Fibonacci numbers are a sequence of numbers named after Leonardo of Pisa, known as Fibonacci (a contraction of filius Bonaccio, "son of Bonaccio"). Fibonacci's 1202 book Liber Abaci introduced the sequence to Western European mathematics, although the sequence had been previously described in Indian mathematics.
The first number of the sequence is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself, yielding the sequence 0, 1, 1, 2, 3, 5, 8, etc. In mathematical terms, it is defined by the following recurrence relation:
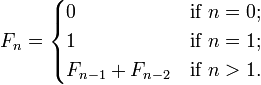
That is, after two starting values, each number is the sum of the two preceding numbers. The first Fibonacci numbers (sequence A000045 in OEIS), also denoted as F[n];
F[n] can be calculate exactly by the following two expressions:
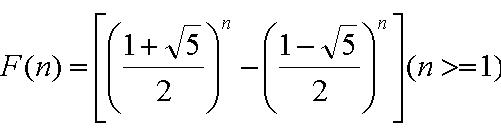
A Fibonacci spiral created by drawing arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34;
So you can see how interesting the Fibonacci number is.
Now AekdyCoin denote a function G(n)
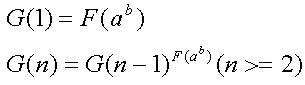
Now your task is quite easy, just help AekdyCoin to calculate the value of G (n) mod C
The first number of the sequence is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself, yielding the sequence 0, 1, 1, 2, 3, 5, 8, etc. In mathematical terms, it is defined by the following recurrence relation:
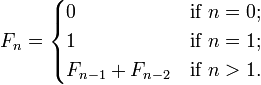
That is, after two starting values, each number is the sum of the two preceding numbers. The first Fibonacci numbers (sequence A000045 in OEIS), also denoted as F[n];
F[n] can be calculate exactly by the following two expressions:
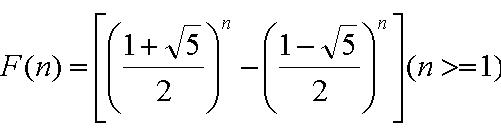
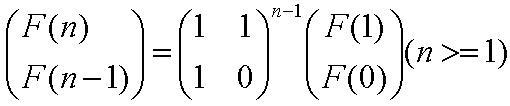
A Fibonacci spiral created by drawing arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34;
So you can see how interesting the Fibonacci number is.
Now AekdyCoin denote a function G(n)
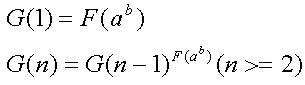
Now your task is quite easy, just help AekdyCoin to calculate the value of G (n) mod C
Input
The input consists of T test cases. The number of test cases (T is given in the first line of the input. Each test case begins with a line containing A, B, N, C (10<=A, B<2^64, 2<=N<2^64, 1<=C<=300)
Output
For each test case, print a line containing the test case number( beginning with 1) followed by a integer which is the value of G(N) mod C
Sample Input
1
17 18446744073709551615 1998 139
Sample Output
Case 1: 120
Author
AekdyCoin
Source
找循环节的思路。
以后要重写一次才行。
1 #include<iostream> 2 #include<stdio.h> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cstring> 6 using namespace std; 7 typedef unsigned __int64 LL; 8 9 bool Hash[303]; 10 LL tom[310],tlen; 11 LL f[3006],hlen; 12 LL sum_mod(LL a,LL n,LL p) 13 { 14 LL ans=0; 15 a=a%p; 16 n=n%p; 17 while(n) 18 { 19 if(n&1) ans=(ans+a)%p; 20 n=n>>1; 21 a=(a+a)%p; 22 } 23 return ans; 24 } 25 LL pow_mod(LL a,LL n,LL p) 26 { 27 LL ans=1; 28 a=a%p; 29 while(n) 30 { 31 if(n&1) ans=sum_mod(ans,a,p); 32 n=n>>1; 33 a=sum_mod(a,a,p); 34 } 35 return ans; 36 } 37 LL Euler(LL n) 38 { 39 LL temp = n,i; 40 for(i=2;i*i<=n;i++) 41 { 42 if(n%i==0) 43 { 44 while(n%i==0) 45 n=n/i; 46 temp=temp/i*(i-1); 47 } 48 } 49 if(n!=1) temp=temp/n*(n-1); 50 return temp; 51 } 52 LL get(LL a,LL b,LL mod)/** F(a^b) % mod**/ 53 { 54 LL i; 55 f[0]=0; 56 f[1]=1; 57 for(i=2;i<3000;i++)//把i<3000去掉,居然RE。 58 { 59 f[i]=(f[i-1]+f[i-2])%mod; 60 if(f[i-1]==0 && f[i]==1) 61 { 62 hlen=i; 63 break; 64 } 65 } 66 hlen--; 67 LL ans = pow_mod(a,b,hlen); 68 if(ans==0)ans=ans+hlen; 69 return f[ans]; 70 } 71 LL solve(LL a,LL b,LL n,LL c) 72 { 73 LL phi = Euler(c); 74 LL AA = get(a,b,c); 75 LL BB = get(a,b,phi); 76 77 LL ans=pow_mod(BB,(n-1),phi)+phi; 78 AA = pow_mod(AA,ans,c); 79 return AA; 80 } 81 int main() 82 { 83 int T,t; 84 LL a,b,n,c; 85 scanf("%d",&T); 86 for(t=1;t<=T;t++) 87 { 88 scanf("%I64u%I64u%I64u%I64u",&a,&b,&n,&c); 89 if(c==1) 90 { 91 printf("Case %d: 0\n",t); 92 continue; 93 } 94 printf("Case %d: %I64u\n",t,solve(a,b,n,c)); 95 } 96 return 0; 97 }
