hdu 2815 Mod Tree

Mod Tree

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3543    Accepted Submission(s): 917


Problem Description

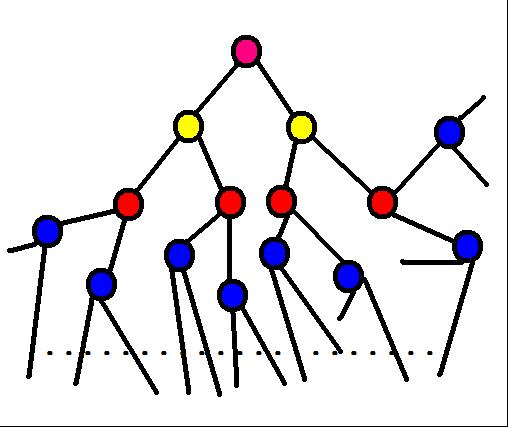
  The picture indicates a tree, every node has 2 children.
  The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
  Now out problem is so easy, give you a tree that every nodes have K children, you are expected to calculate the minimize depth D so that the number of nodes whose depth is D equals to N after mod P.
 

 

Input
The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)
 

 

Output
The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”
 

 

Sample Input
3 78992 453 4 1314520 65536 5 1234 67
 

 

Sample Output
Orz,I can’t find D! 8 20
 

 

Author
AekdyCoin
 

 

Source
HDU 1st “Old-Vegetable-Birds Cup” Programming Open Contest
 

 

Recommend
lcy
 
 
题目意思 k^x (mod P) =  N
1.当N>=P,显然无解。
2.当P=1  ,显然为0。
为什么上一题poj3243那题 没有讨论这个呢。
上一题的意思是 A^x % C = B % C ,所以没有1的判断
 
这道题的输出很坑的，要特别注意。
 
  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstdlib>
  4 #include<cstring>
  5 #include<cmath>
  6 using namespace std;
  7 const int MAX=499991;
  8 typedef __int64 LL;
  9 LL A,B,C;
 10 bool Hash[MAX];
 11 LL val[MAX];
 12 LL idx[MAX];
 13 
 14 LL gcd(LL a,LL b)
 15 {
 16     if(b==0)
 17     return a;
 18     return gcd(b,a%b);
 19 }
 20 
 21 void Ex_gcd(LL a,LL b,LL &x,LL &y)
 22 {
 23     if(b==0)
 24     {
 25         x=1;
 26         y=0;
 27         return ;
 28     }
 29     Ex_gcd(b,a%b,x,y);
 30     LL hxl=x-a/b*y;
 31     x=y;
 32     y=hxl;
 33     return ;
 34 }
 35 
 36 void Insert(LL id,LL num)//哈希建立
 37 {
 38     LL k=num%MAX;
 39     while(Hash[k] && val[k]!=num)
 40     {
 41         k++; if(k==MAX) k=k-MAX;
 42     }
 43     if(!Hash[k])
 44     {
 45         Hash[k]=true;
 46         val[k]=num;
 47         idx[k]=id;
 48     }
 49     return;
 50 }
 51 
 52 LL found(LL num)//哈希查询
 53 {
 54     LL k=num%MAX;
 55     while(Hash[k] && val[k]!=num)
 56     {
 57         k++;
 58         if(k==MAX) k=k-MAX;
 59     }
 60     if(Hash[k])
 61     {
 62         return idx[k];
 63     }
 64     return -1;
 65 }
 66 
 67 LL baby_step(LL a,LL b,LL c)
 68 {
 69     LL temp=1;
 70     for(LL i=0;i<=100;i++)
 71     {
 72         if(temp==b) return i;
 73         temp=(temp*a)%c;
 74     }
 75     LL tmp,D=1,count=0;
 76     memset(Hash,false,sizeof(Hash));
 77     memset(val,-1,sizeof(val));
 78     memset(idx,-1,sizeof(idx));
 79 
 80     while( (tmp=gcd(a,c))!=1 )
 81     {
 82         if(b%tmp) return -1;
 83         c=c/tmp;
 84         b=b/tmp;
 85         D=D*a/tmp%c;
 86         count++;
 87     }
 88     LL cur=1;
 89     LL M=ceil(sqrt(c*1.0));
 90     for(LL i=1;i<=M;i++)//初始的时候，i=0开始，错了。！！？
 91     {
 92         cur=cur*a%c;
 93         Insert(i,cur);
 94     }
 95     LL x,y;
 96     for(LL i=0;i<=M;i++)
 97     {
 98         Ex_gcd(D,c,x,y);
 99         x=x*b%c;
100         x=(x%c+c)%c;
101         LL k=found(x);
102         if(k!=-1)
103         {
104             return i*M+k+count;
105         }
106         D=D*cur%c;
107     }
108     return -1;
109 }
110 
111 int main()
112 {
113     while(scanf("%I64d%I64d%I64d",&A,&C,&B)>0)
114     {
115         if(B>=C)
116         {
117             printf("Orz,I can’t find D!\n");
118             continue;
119         }
120         if(C==1)
121         {
122             printf("0\n");
123             continue;
124         }
125         LL cur=baby_step(A,B,C);
126         if(cur==-1)
127         {
128             printf("Orz,I can’t find D!\n");
129         }
130         else printf("%I64d\n",cur);
131     }
132     return 0;
133 }

 

posted @ 2013-08-27 08:48  芷水  阅读(265)  评论(0)  编辑  收藏  举报