Python 基础第十五天(递归函数和二分查找)

今日主要内容

1.递归函数

2.二分查找

 

今日主要对以上内容进行初步的了解.下面简单介绍:

递归函数

1)初识递归

什么是递归函数:

递归函数：在一个函数里在调用这个函数本身

递归的最大深度：998

正如你们刚刚看到的，递归函数如果不受到外力的阻止会一直执行下去。但是我们之前已经说过关于函数调用的问题，每一次函数调用都会产生一个属于它自己的名称空间，如果一直调用下去，就会造成名称空间占用太多内存的问题，于是python为了杜绝此类现象，强制的将递归层数控制在了997(只要997！你买不了吃亏，买不了上当...).

拿什么来证明这个“998理论”呢？这里我们可以做一个实验：

由此我们可以看出，未报错之前能看到的最大数字就是998.当然了，997是python为了我们程序的内存优化所设定的一个默认值，我们当然还可以通过一些手段去修改它：

import sys
print(sys.setrecursionlimit(100000))

递归示例讲解

现在你们问我，alex老师多大了？我说我不告诉你，但alex比 egon 大两岁。

你想知道alex多大，你是不是还得去问egon？egon说，我也不告诉你，但我比武sir大两岁。

你又问武sir，武sir也不告诉你，他说他比太白大两岁。

那你问太白，太白告诉你，他18了。

这个时候你是不是就知道了？alex多大？

1	金鑫	18
2	武sir	20
3	egon	22
4	alex	24

你为什么能知道的？

首先，你是不是问alex的年龄，结果又找到egon、武sir、太白，你挨个儿问过去，一直到拿到一个确切的答案，然后顺着这条线再找回来，才得到最终alex的年龄。这个过程已经非常接近递归的思想。我们就来具体的我分析一下，这几个人之间的规律。

age(4) = age(3) + 2 
age(3) = age(2) + 2
age(2) = age(1) + 2
age(1) = 40

那这样的情况，我们的函数怎么写呢？

def age(n):
    if n == 1:
        return 40
    else:
        return age(n-1)+2

print(age(4))

 

二分查找法

举例说明:

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

你观察这个列表，这是不是一个从小到大排序的有序列表呀？

如果这样，假如我要找的数比列表中间的数还大，是不是我直接在列表的后半边找就行了？

 

 

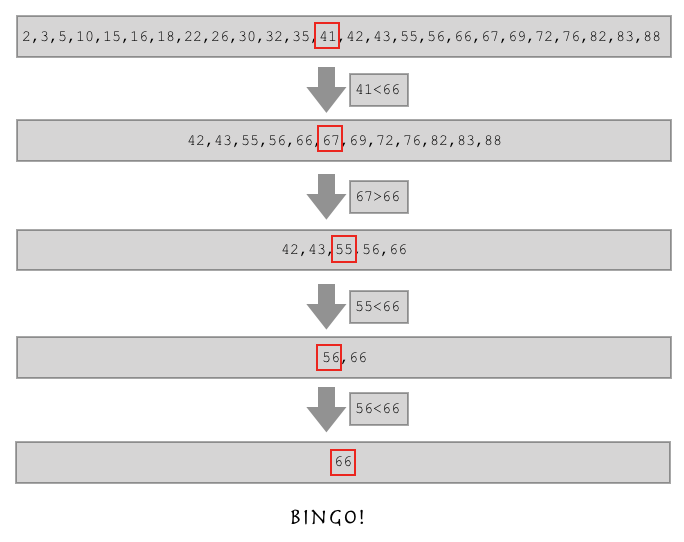
这就是二分查找算法！

那么落实到代码上我们应该怎么实现呢？ 

简单版二分法

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

def func(l,aim):
    mid = (len(l)-1)//2
    if l:
        if aim > l[mid]:
            func(l[mid+1:],aim)
        elif aim < l[mid]:
            func(l[:mid],aim)
        elif aim == l[mid]:
            print("bingo",mid)
    else:
        print('找不到')
func(l,66)
func(l,6)

升级版二分法

def search(num,l,start=None,end=None):
    start = start if start else 0
    end = end if end else len(l) - 1
    mid = (end - start)//2 + start
    if start > end:
        return None
    elif l[mid] > num :
        return search(num,l,start,mid-1)
    elif l[mid] < num:
        return search(num,l,mid+1,end)
    elif l[mid] == num:
        return mid