自动控制理论笔记
经典控制理论
动态系统建模
通过配置系统输入u(t),使u(s)G(s)的极点使系统满足一定特性
一阶系统特性
\(G(s) = \frac{a}{s+a}\)
\(\frac{1}{a}\)是时间常数\(\tau\),对应上升为0.63
\(4\tau\)对应阶跃响应0.98
二阶系统特性
\(m\ddot x+B\dot x+kx=F\)
\(\ddot x+2\omega_n\xi \dot x+\omega_n^2x=\frac{F}{m}\)
阻尼比固有频率:\(\omega_n\sqrt{1-\xi^2}\)
单位化:\(u(t)=\frac{F}{\omega_n^2}\)
\(H(s) = \frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2}\)

零极点图:
极点全部在左,系统稳定
虚轴长度代表振荡周期
实轴长度代表衰减速度
\(\cos \theta\)代表阻尼比
SISO system稳定性判据
特征多项式系数判断传递函数稳定性
- Hurwitz霍尔维兹判据:构建霍尔维兹行列式,全部为正
\(D1 = a_1\)
\(D2 = \begin{pmatrix}
a_1&a_3\\
a_0&a_2
\end{pmatrix}\)
\(D3 = \begin{pmatrix}
a_{1}& a_{3}& a_{5}\\
a_{0}& a_{2}& a_{4}\\
0& a_{1}& a_{3}
\end{pmatrix}\)
- Lienard-Chipard林纳德-齐帕特判据:系数都大于零,奇数或偶数阶次行列式
- Routh劳斯判据:
求\(e_{ss}\)时顺序,1判断稳定性、2求E(s),3应用终值定理\(e_{ss} = \lim \limits_{s\rightarrow0}sE(s)\) - 频率稳定判据:
H. Nyquist奈奎斯特判据,开环频率特性,判断闭环稳定性
\(F(s) = 1 +G(s)H(s)\)的p,极点,是开环传函极点
z零点,闭环传递函数的极点封闭曲线内\(R=P-Z\)
频率特性
- 只适用于线性定常模型,否则不能拉式变换
- 稳定条件下使用
bode图单位用dB:20log(Mo/Mi),表征了能量
- 幅值相应:magnitude response
\(\frac{M_o}{M_i} = \left | G(j\omega)\right |\) - 幅角响应:Phase response
\(\phi_o-\phi_i = \angle G(j\omega)\) 带阻尼比的共振频率:
\(\omega = \omega_n \sqrt{1-2\zeta^2}\\\)
此时的极值:\(\frac{1}{2\zeta\sqrt{1-\zeta^2}}\)幅值裕度h:相位为-π时,幅值距0dB的差值
相位裕度\(\gamma\):幅值为1(0dB)时,相位距-π的差
根据幅相图,(0,0)出发为开环,(-1,0)出发为闭环不同频段信息
- 低频段\(G(j\omega)\)反映了系统的稳态精度
0dB/sec->稳态精度 - 中频段:穿越0dB\(\omega_c\)
反映了系统的平稳性和快速性
-20dB/sec开环积分,闭环一阶,快速性
-40dB/sec开环双积分,闭环二阶,零阻尼,频率段不宜过宽,穿越频率取-20斜率 - 高频段反映了系统对高频干扰抑制能力
系统矫正
串联矫正
超前矫正
\(G_c(s)=\frac{1+aTs}{1+Ts},a>1\)滞后矫正
\(G_c(s)=\frac{1+bTs}{1+Ts},b<1\)滞后超前矫正
两个合起来PID矫正器
复合矫正
前置矫正:指令->Gc(s)->误差,一般补偿分母s,开环前向增益1
干扰前置补偿:干扰测量->Gc(s)->误差,误差->干扰端传函\(Gs^{-1}\)
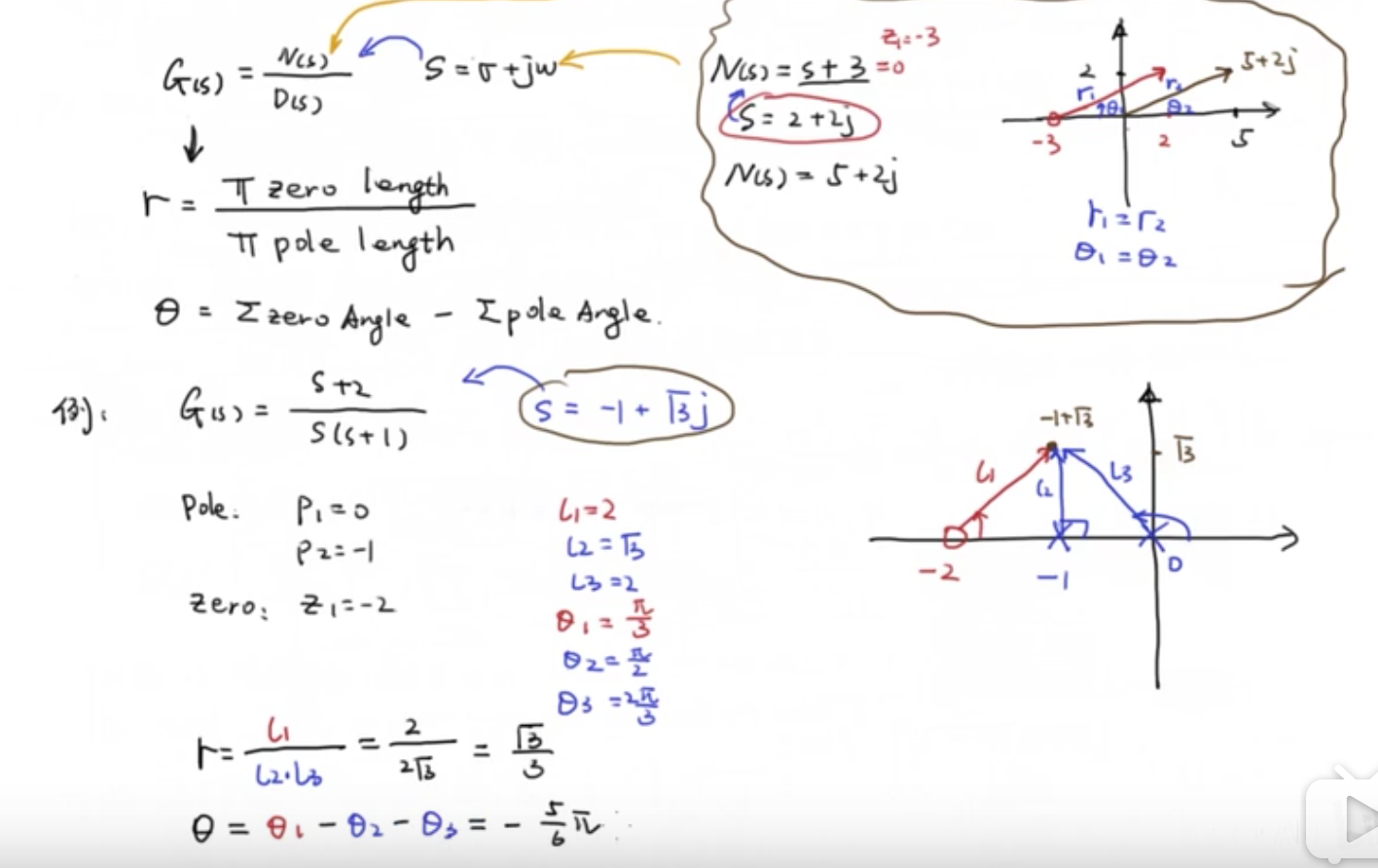
根轨迹
(开环->闭环稳定性):分析G(s)的N、P,看闭环系统稳定性
开环传递函数中开环增益K从0-无穷时,闭环特征根的移动轨迹
单位负反馈闭环传递函数
\(\phi(s) = \frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}\)
G(s)是一个
非线性系统
叠加原理不适用
常规分类:
死区
饱和
间隙-滞环
系统收敛:消耗系统能量
系统发散:从外界获取能量
相关词汇
\(X_{ss}(t)\):ss-steady state
\(T_s\)Delay time
\(T_r\)Rise time
\(M_p\)Max Overshoot
\(T_{ss}\)Setting time调节时间
BIBO:输入稳定,输出稳定bounded input-bounded output
Real:实轴
Im:虚轴
Proportional:比例
Integral:积分
Differential:微分
bounded input-bounded output:稳定性
\(\forall\)for all :任意
\(\exists\) at least one :存在
\(\left \| \cdot \right \|\)norm:范数
工程数学基础
1. 特征值,特征向量,过渡矩阵\(\rightarrow\)矩阵对角化
特征值\(\lambda\)有\(\lambda v=Av\)
\(\ | \lambda I-A\ | = 0\)
特征值
解法:将\(\lambda\)代回\(( \lambda I - A)* v = 0\)
\(\lambda_1 、\lambda_2\)对应特征向量\(v_1 、v_2\)
过渡矩阵:特征向量组成的矩阵
\(P =
\begin {pmatrix} v_1&v_2
\end {pmatrix}\)
\(AP=A[v_1 v_2] = [Av_1 Av_2]=[\lambda_1v_1 \lambda_2 v_2]=
\begin{bmatrix}
\lambda_1v_{11} & \lambda_2v_{21}\\
\lambda_1v_{12} & \lambda_2v_{22}
\end{bmatrix}
=P\Lambda
\)
所以有,单位向量矩阵P将A特征值对角化矩阵
\(P^-1AP = \Lambda\)
2. 线性化 Linearization
非线性:\(1/x,\sqrt{x},x^n等\)
用泰勒级数展开
在平衡点(Fixed point)\(x_0\)附近线性化
- 令导数项为0,求得平衡点x的值\(x=x_0\)
- 把\(x_\sigma = x_0 + x_d\)代入\(f(x_\sigma)=f(x_0)+f'(x_0)(x_\sigma-x_0)\)
- 把\(x = x_\sigma\)代入微分方程
将\(\sigma\)的x用x_0和x_d替换,然后
得到了关于x_d的线性化微分方程
\(\dot x = A x + b u\)求A的雅可比矩阵
行是函数,列为对变量的偏导;
求平衡点,代入偏导雅可比矩阵;
展开得到线性化后的微分方程
3. 卷积与LTI冲激响应(LTI:linear time invariant system)
卷积:\(x(t) = f(t)*h(t)=\int_0^t f(\tau)h(t-\tau)d\tau\)
\(f(t)\)=输入
\(h(t)\)=单位冲激响应
\(L_{卷积}\)=L乘积
4. 欧拉公式Euler's Formula
\(e^{i\theta}=\cos(\theta)+i\sin(\theta)\)
5. 复数Complex Number
\(\sin(x) = C\rightarrow x = \pi/2+2k\pi + \ln(C\pm\sqrt{C^2-1})i\)
\(Z = a + b i \)
\(Re(Z) =a \)
\(Im(Z)=b \)
\(\left | Z \right | = \sqrt{a^2+b^2}\)
\(Z = \left | Z \right | \cdot (\cos\theta+i\sin\theta)= \left | Z \right | \cdot e^{i\theta}\)
\(Z_1 \cdot Z_2 = \left | Z_1 \right | \left | Z_2 \right | e^{\theta_1+\theta_2}\)
\(Z+\bar Z = 2a\)
\(Z- \bar Z = 2bi\)
6. 阈值选取
Normal Distribution正态分布、高斯分布
\(X = (\mu,\sigma^2)\)
漏检False Dismissal
误警False Alarm
Advanced控制理论
状态空间:State-Space,包含输入、输出、状态,写成一阶微分方程的形式
\(\dot x = A x + B u\)
\(y = Cx+Du\)
稳定性
两种类型
Lyapunov稳定性:有界
\(\forall t_0, \forall \epsilon >0, \exists \delta (t_0, \epsilon):\left \| x(t_0)\right \|<\delta(t_0,\epsilon)\Rightarrow \forall t \geqslant t_0, \left \| x(t) \right \| < \epsilon\)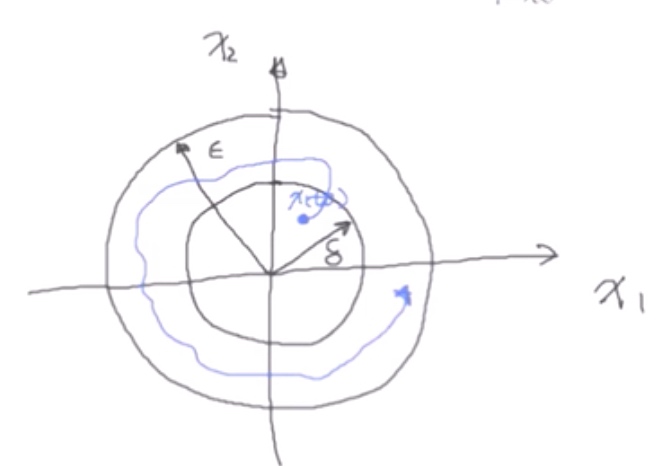
\(a \, of\, \lambda_i \leqslant 0\)实部
判断方法:渐进稳定性:
\(\exists \delta(t_0)>0: \left \|x(t_0)\right \|<\delta(t_0) \Rightarrow
\lim \limits_{t \rightarrow \infty }
\left \| x(t)\right \| = 0
\)
\(a \, of\, \lambda_i < 0\)实部
判别方法
- 直接方法:解微分方程(Direct method)
求解λ的值,判断正负 - 第二方法:(2nd method)
\((i)V(0) = 0\)
\((ii) V(x) \geqslant 0 , in\, D-{0}\) PSD:postive semi definit
\((iii)\dot V(x) \leqslant 0 , in\, D-{0}\)NSD:negative semi definit
\(\Rightarrow x = 0\)
3. 不稳定
存在至少一个特征值实部大于零
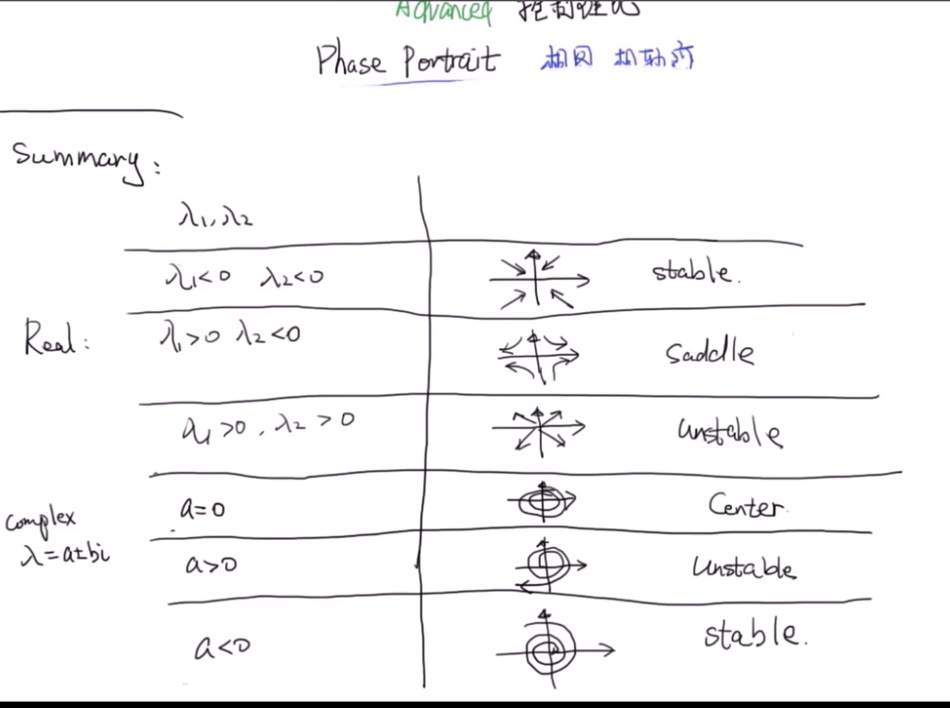
相图分析-phase-portrait
plot(x,\(\dot x\)),通过x初值,分析点在轨迹上的移动,判断稳不稳定
matlab绘制实例
% 画解微分方程组的相图
clear;cla;clc;
[x,y]=meshgrid(linspace(-5,5));
streamslice(x,y,0 * x + 2 * y,-3 * x + 0 * y );
xlabel('x');ylabel('y');
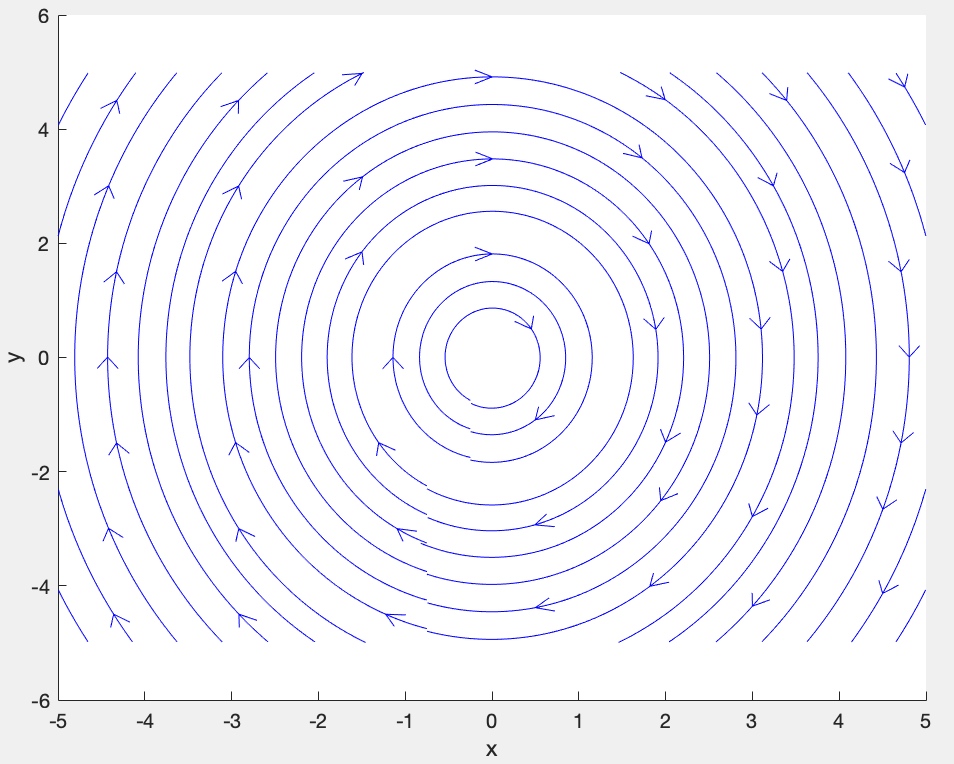
特征值和相图的关系
齐次状态方程解\(\dot x = A x\)
\(\dot x = a x\rightarrow x(t) = e^{at}x(0)\)
同理,多元线性方程
\(\dot x = a x\rightarrow x(t) = e^{At}x(0)\)
其中,状态转移矩阵\(\Phi(t)\)解法
- 数值法:
\(\Phi(t) = e^{At}=I+At+\frac{1}{2!}A^2t^2+...+\frac{1}{k!}A^kt^k\) - 解析法:
\(\Phi(t) = L^{-1}[sI-A]^{-1}\)
性质:
\(\Phi(0) = I\)
\(x(t) = \Phi(t-t_0)x(t_0)\)
\(\Phi ^{-1}(t) = \Phi(-t)\)
非齐次状态方程\(\dot x = A x + B u\)
\(x(t) = \Phi (t)x(0)+ \int_0^t\Phi(t-\tau)Bu(\tau)d\tau\)
初始状态x(0)响应+输入项u(t)响应
线性系统可控性与可观测性
可控性:\(\forall x(0),x(t_f), \exists t_f < +\infty , u[0,t_f], st. x(0)\rightarrow x(t_f)\)
充要条件:
\(S = [b\, Ab\, A^2...\, A^{n-1}b]\)
理论可行,但是实际物理不一定
以离散系统为例证明:
\(x_ 0 = 0\\
x_1 = Ax_0 + Bu_0 = Bu_0\\
x_2 = Ax_1 + Bu_1 = ABu_0 + B u_1\\
x_3 = Ax_2 + Bu_2 = A^2Bu_0 + AB u_1 + B u_2\\
\)
Matlab 求解,Co矩阵 "ctrb(A,B)"\(rank[S] = n, det \, S \neq 0\)
可观性:\(\forall t \in [t_0,t_f],已知y(t),u(t),可求x(t_0)\)
\(rank
\begin{bmatrix}
C\\
CA\\
CA^2\\
...\\
CA^{n-1}
\end{bmatrix}
=n
\)
引理
\(f(\lambda) = \sum_{i=0}^{n}a_i\lambda ^i\)
\(f(A) = 0 \rightarrow A^n = \sum_{i=0}^{n-1}a_iA^i\)
求解\(\left | \lambda I - A\right |\)的特征多项式
将\(\lambda = A \)代入,得到递推公式,解算\(A^n\)
状态反馈与状态观测器
取\(u=v-kx\),其中,v为参考输入,系统闭环矩阵由A变为A-Bk
- 不改变可控性,有可能改变可观性
- 闭环特征值
状态观测器
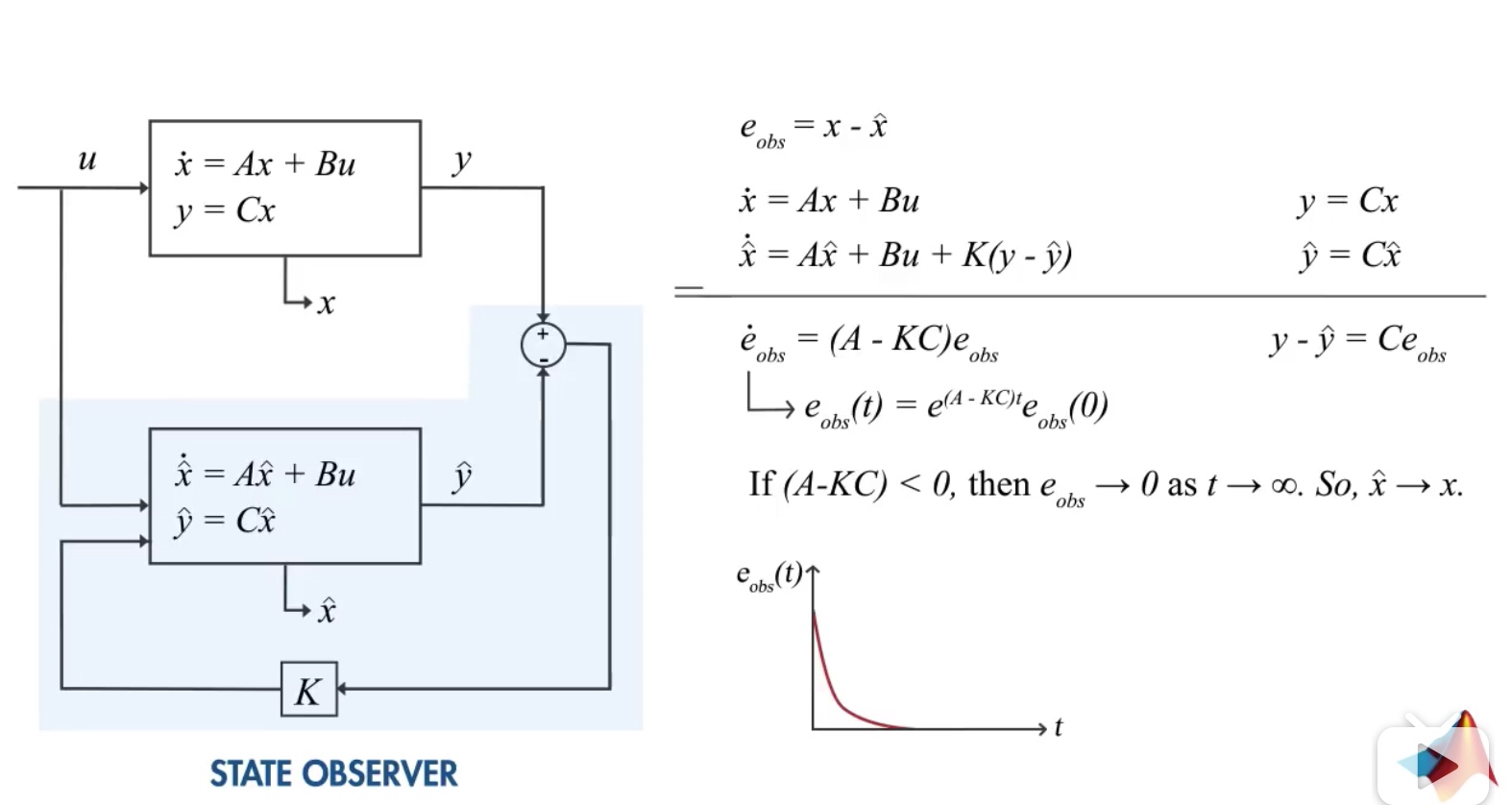
Kalman滤波器原理以及在matalb中的实现
状态转移矩阵:
这里要改一下,改成估计量
\(x_t^- = F_t x_{t-1} + B_t u_t\)
状态转移矩阵:\(P_t^-=FP_{t-1}F^T+Q\)
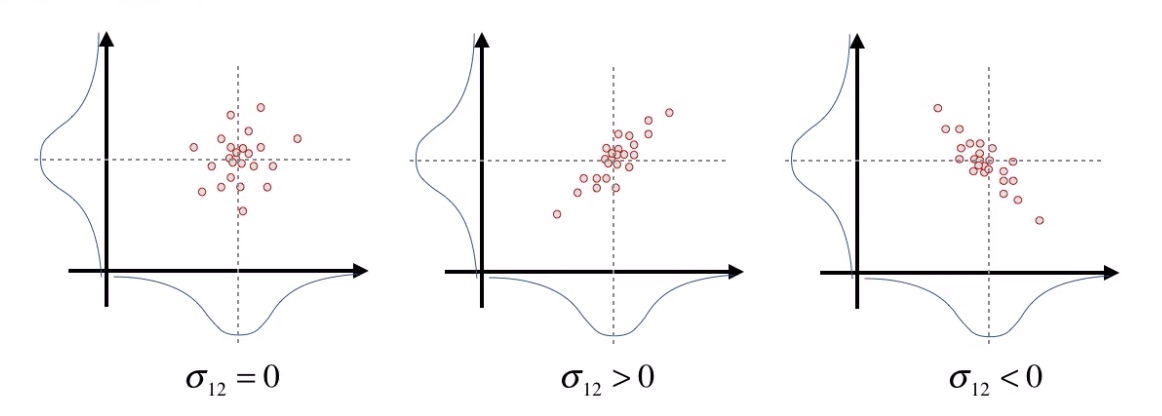
协方差矩阵:
\(
\begin{bmatrix}
\sigma_{11}&\sigma_{12}\\
\sigma_{12}&\sigma_{22}\\
\end{bmatrix}
\)
卡尔曼方程≠状态观测器
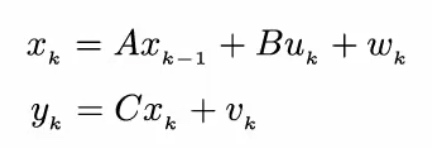
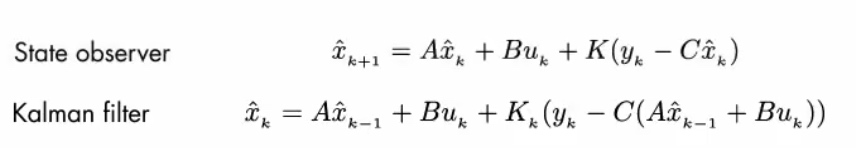
以小车为例,讲卡尔曼滤波最优状态估计
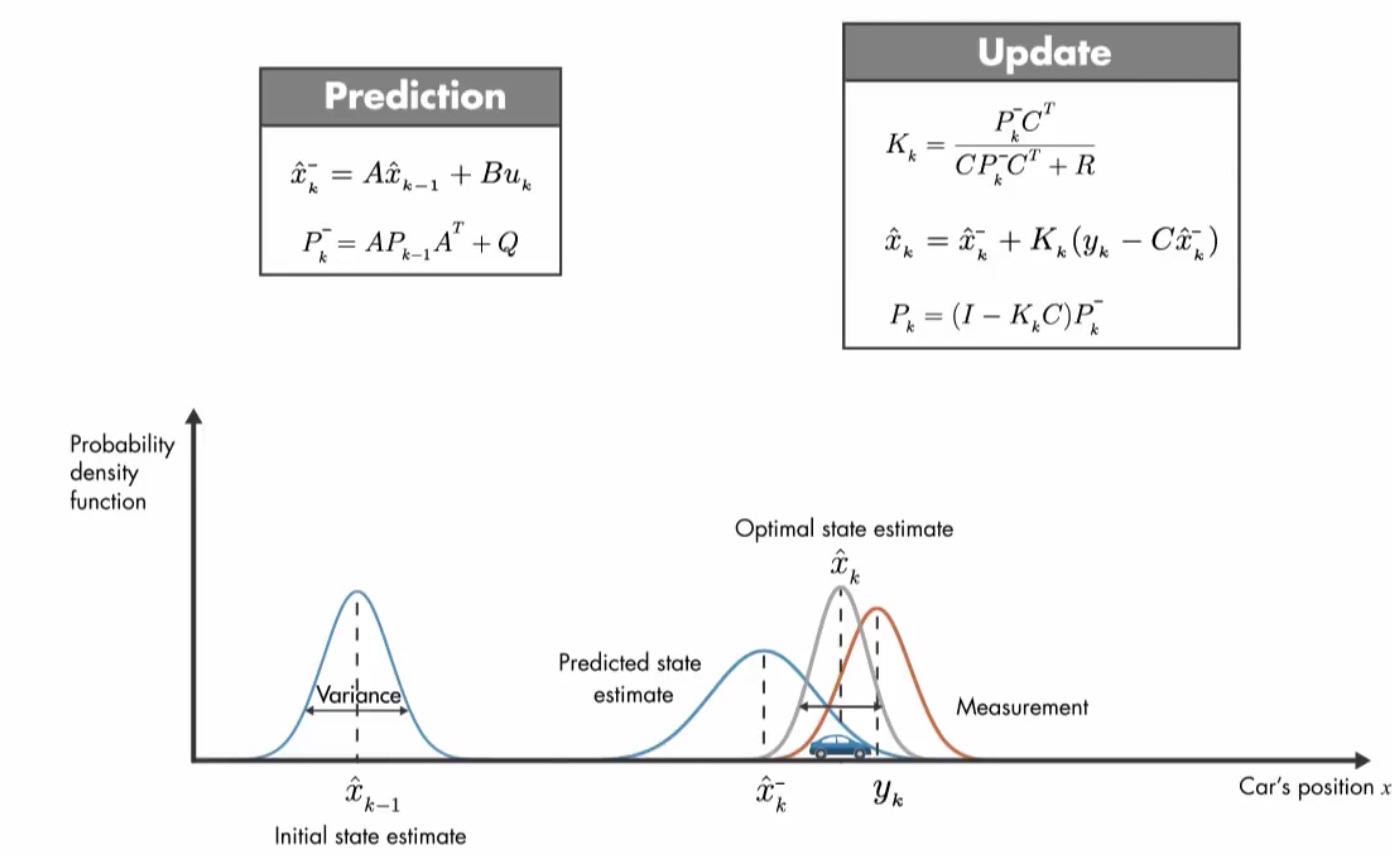
在上图中,P是观测值\(\hat x\)的方差
R是观测器中,来自预估值的比例
概率函数相乘,多传感器信息融合
非线性控制理论
ARC
Barbalat’s 引理 lemma
- \(V\geq0\)
- \(\dot{V} \leq -g(t)\), where \(g(t)\geq 0\)
- \(\dot{g}(t)\in L_{\infty}\), if\(\dot{g}(t)\) is bounded the g(t) is uniformly continous.
Then, \(\lim_{t->\infty} g(t)=0\)
Consquently, \(\lim_{t->\infty} e = 0 (k\neq0)\)

