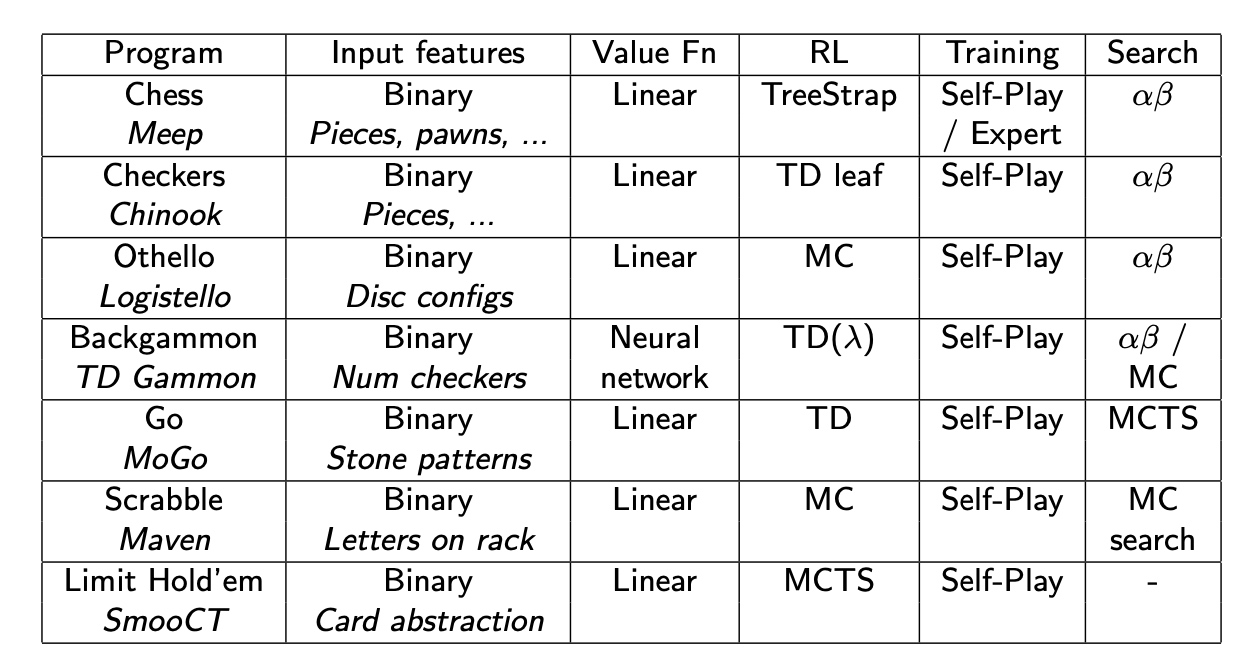
强化学习笔记10：经典游戏示例 classic games

1、前沿 state of art

学习经典游戏的原因

  • 规则简单，细思又很深入
  • 历史悠久，已经被研究了几百年
  • 对IQ测试有意义
  • 是现实世界的问题的缩影

已经有很多RL案例，战胜了人类，例如

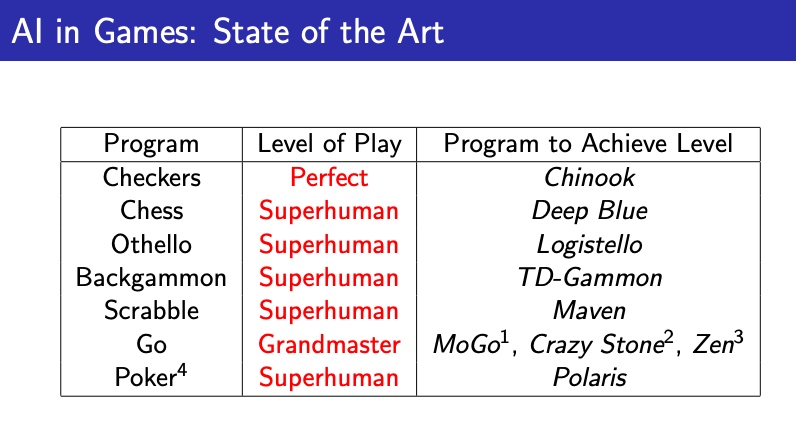
2、游戏理论 game theory

游戏的最优性

对于石头剪刀布来说，最优策略，显然和对手agent策略相关，我们期望找到一种一致的策略策略，对所有对手都有效
什么是第i个玩家的最优策略\(\pi\)

  • 最佳响应 best response \(\pi^i_*(\pi^{-i})\) 是针对其他agent的最优策略
  • 纳什平衡点 Nash equilibrium是针对所有对手的联合策略 \[
    \pi^i = \pi^i_*(\pi^{-i})\]

对于agent来说的最优策略，是一种general 的 策略，对大多数情况，都适用一致的策略去action.

单agent 自驱动 强化学习

  • 最佳响应 是 单代理RL问题的解决方案
    • 其他玩家 变成环境的一部分
    • 将游戏 抽象为MDP
    • 最佳策略是 最佳响应
  • 纳什平衡点 在 自学习RL问题中是 不动点
    • 学习的经验是 代理玩游戏产生的
      \[a_{1} \sim \pi^{1}, a_{2} \sim \pi^{2}, \ldots\]
    • 每个代理学习针对其他玩家的最佳响应
    • 代理的策略决定了其他代理的环境
    • 所有的代理适应其他代理

二人零和博弈游戏

收益来自其他agent，一方受益，意味着其他亏损

\[R^1 + R^2 = 0\]

methods for finding 纳什平衡点

  • Game tree search （i.e. planning）
  • 自驱动RL

perfect and imperfect information games

  • 完美信息或者 马尔科夫游戏是 完全可观的
    • 象棋
    • 围棋
    • 跳棋
    • 五子棋
  • 不完全信息游戏是部分可观的
    • 扑克
    • 拼图

3、最小、最大搜索

introduction

  • 价值函数定义了策略\(\pi\)下的价值
    \[
    v\pi(s) = \mathcal E_\pi [G_t|S_t= s]\]

  • 最小、最大化价值函数，是在降低其他代理表现的同时，最大化自己的价值

\[
v_{*}(s)=\max _{\pi^{1}} \min _{\pi^{2}} v_{\pi}(s)
\]

  • 最小、最大搜索存在纳什平衡点

  • 通过深度优先树搜索，找到极值


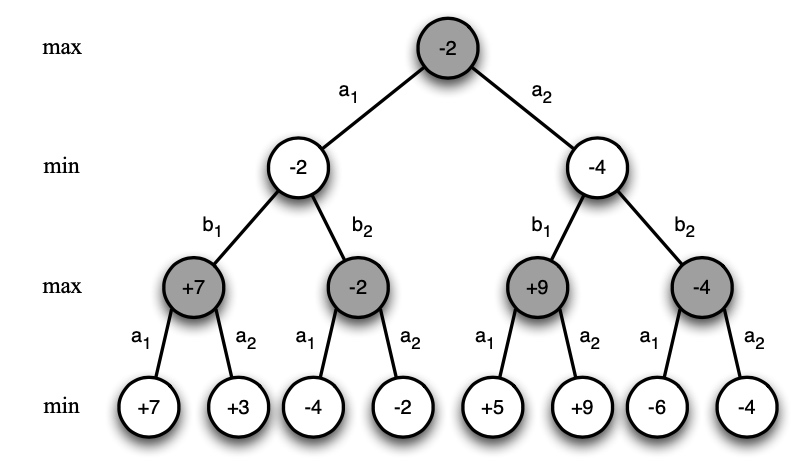
从下往上找：
一步找max，一步找min
缺点是，运算量指数增长，不能求解整个树的分支
Solution：

  • 用值函数估计器，估计叶节点
  • 根据节点值，限制搜索深度

Example

二进制 线性组合 值函数

  • 每 个状态特征，只有0、1
  • 每个特征对应权重 w
  • 线性组合

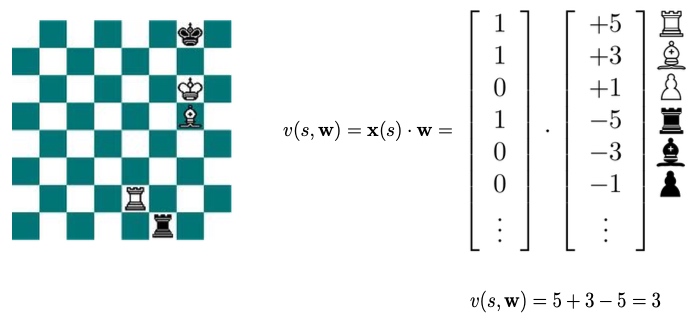
深蓝 Deep blue，并不是真正的学习，手动权重

  • 知识 Knowledge
    • 8k个手动特征
    • 二进制线性组合价值函数
    • 人工个调参 权重
  • 搜索 Search
    • 高性能平行字母搜索
    • 40步预测
    • 每秒
  • 结果 Results
    • 击败了世界冠军

Chinook

  • 知识 Knowledge
    • 二进制线性组合价值函数
    • 21个经验权重（位置、流动性）
    • 四象限
  • 搜索 Search
    • 高性能平行字母搜索
    • 逆向搜索
      • 从赢的位置从后向前搜索
      • 存储所有决胜点位置在 lookup 表中
      • 在最后n步，表现完美
  • 结果 Results
    • 击败了世界冠军

4、自驱动强化学习 self-play reinforcement learning

Introduction

应用 Value-based RL，完成游戏自学

  • MC 向\(G_t\)更新
    \[\Delta \mathbf{w}=\alpha\left(G_{t}-v\left(S_{t}, \mathbf{w}\right)\right) \nabla_{\mathbf{w}} v\left(S_{t}, \mathbf{w}\right)\]

  • TD（0）向\(v(s_t +1)\)更新
    \[\Delta \mathbf{w}=\alpha\left(v\left(S_{t+1}, \mathbf{w}\right)-v\left(S_{t}, \mathbf{w}\right)\right) \nabla_{\mathbf{w}} v\left(S_{t}, \mathbf{w}\right)\]

  • TD（\(\lambda\)）向\(\lambda\)-return \(G_t^\lambda\)更新
    \[\Delta \mathbf{w}=\alpha\left(G_{t}^{\lambda}-v\left(S_{t}, \mathbf{w}\right)\right) \nabla_{\mathbf{w}} v\left(S_{t}, \mathbf{w}\right)\]

策略提升 Policy improvement

规则的定义决定了后继者的状态 \(succ(s,a)\)

对于确定性的游戏，估计价值函数是足够的
\[
q_*(s,a) = v_*(succ(s,a))\]

同样采用最小最大优化

\[ A_{t}=\underset{a}{\operatorname{argmax}} v_{*}\left(\operatorname{succ}\left(S_{t}, a\right)\right)
\ for\ white\\
A_{t}=\underset{a}{\operatorname{argmin}} v_{*}\left(\operatorname{succ}\left(S_{t}, a\right)\right)
\ for\ black\]

Self-play TD in Othello： logistello

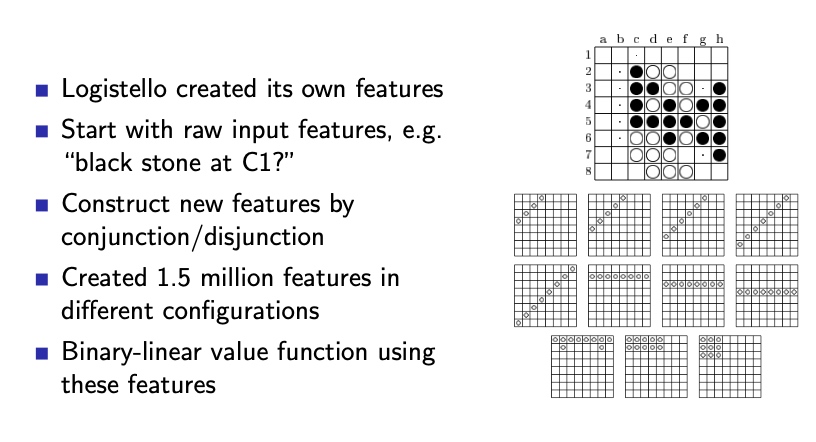
使用了策略迭代的方法：

  • 用2个代理进行对抗
  • 用MC 评估 策略
  • Greedy 策略优化

6：0战胜世界冠军

TD Gammon: 非线性价值函数估计

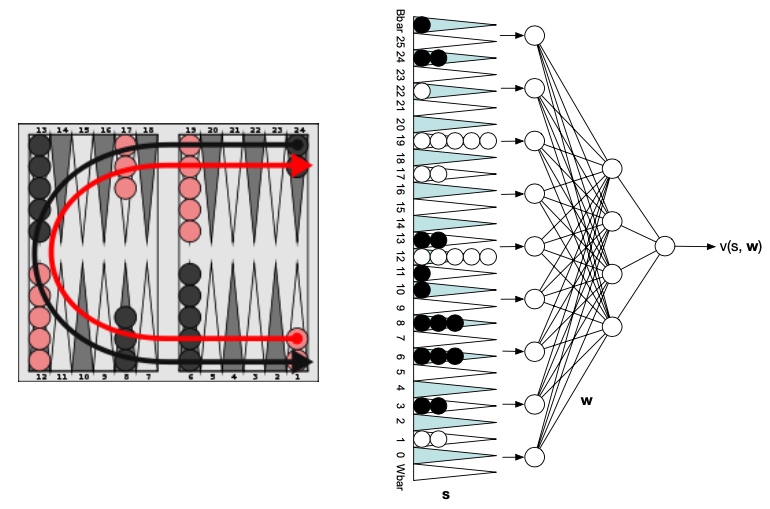
自学习 TD 在西洋双陆棋 Backgammon

  1. 权重随机初始化
  2. 自学习训练
  3. 使用非线性TD 学习算法
    \[\begin{aligned}
    \delta_{t} &=v\left(S_{t+1}, \mathbf{w}\right)-v\left(S_{t}, \mathbf{w}\right) \\
    \Delta \mathbf{w} &=\alpha \delta_{t} \nabla_{\mathbf{w}} v\left(S_{t}, \mathbf{w}\right)
    \end{aligned}\]
  4. Greedy 策略优化

TD gammon 的几个层级：

  • zero 专家经验
  • 人造特征
  • n层极小极大搜索

隐藏层个数、 训练代数，直接影响模型表现

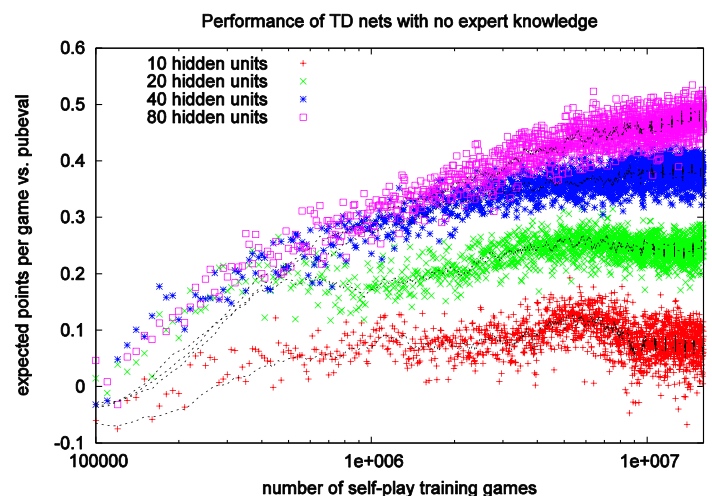
5、联合强化学习和最大化搜索

简单 TD Simple TD

TD：向继承者的方向更新价值函数

分为两步

  • 用TD learning 学习价值函数
  • 用价值函数 进行 最小最大搜索

\[v_{+}\left(S_{t}, \mathbf{w}\right)=\operatorname{minimax}_{s \in \text {leaves}\left(S_{t}\right)} v(s, \mathbf{w})\]

在有些情景表现优异，有些糟糕

TD root

TD root：从继承者 搜索值更新 价值函数

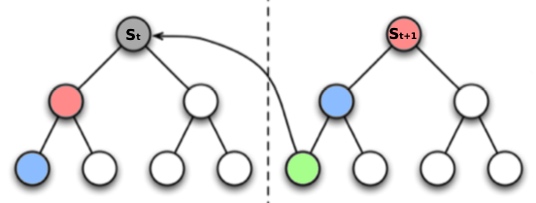
  • 搜索值 根据 根节点计算得到
    \[v_{+}\left(S_{t}, \mathbf{w}\right)=\underset{s \in \text { leaves }}{\operatorname{minimax}} \left(S_{t}\right) v(s, \mathbf{w})\]
  • 从下一个状态的 搜索值 备份 值函数
    \[v\left(S_{t}, \mathbf{w}\right) \leftarrow v_{+}\left(S_{t+1}, \mathbf{w}\right)=v\left(l_{+}\left(S_{t+1}\right), \mathbf{w}\right)\]
  • \(I_+(s)\)是 从状态s 进行极小极大搜索后 的 叶节点值

TD leaf

TD leaf：从继承者的 搜索值 更新 搜索值

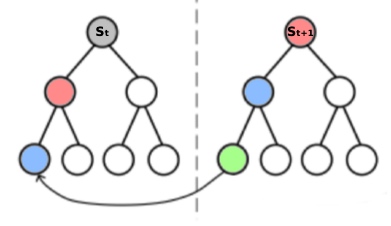
  • 搜索值 由当前和 下一个状态计算得到

这个公式无法显示

v_{+}\left(S_{t}, \mathbf{w}\right)=\underset{{s \in \text { leaves }\left(S_{t}\right)}}{\rm{minimax}} v(s, \mathbf{w})\\
v_{+}\left(S_{t+1}, \mathbf{w}\right)=\underset{{s \in \text { leaves }\left(S_{t+1}\right)}}{\rm{minimax}} v(s, \mathbf{w})

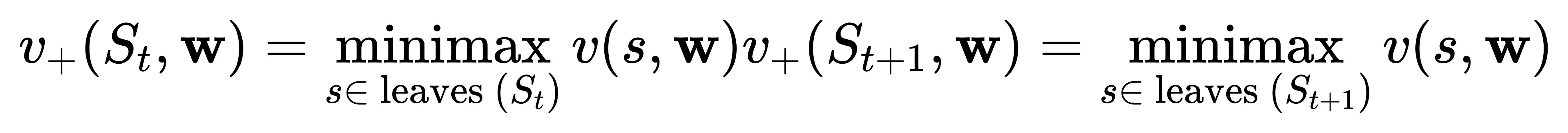
MommyTalk1599040691831
MommyTalk1599040691831

  • t时刻的搜索值 由 t+1时刻的搜索值备份得到
    \[
    \begin{aligned}
    v_{+}\left(S_{t}, \mathbf{w}\right) & \leftarrow v_{+}\left(S_{t+1}, \mathbf{w}\right) \\
    \Longrightarrow v\left(l_{+}\left(S_{t}\right), \mathbf{w}\right) & \leftarrow v\left(l_{+}\left(S_{t+1}\right), \mathbf{w}\right)
    \end{aligned}
    \]

examples：

TD leaf in chess： knightcap

  • learning
    • 训练专家对手
    • 使用TD leaf 学习权重
  • 搜索
    • alpha-beta search
  • Results
    • master level 完成少数的游戏之后
    • 不够高效 in 自学习
    • 不够高效，受初始权重影响较大

TD leaf in Checkers： Chinook

  • 初始的chinook采用手动调优的权重
  • 后来的版本自训练
  • 采用Td leaf 调整权重
    • 固定了专家
  • 自学习权重的表现 ＞ 人工调优权重的表现
  • 超过人类水平

TreeStrap

  • TreeStrap：用深层的搜索值 更新 浅层的 搜索值

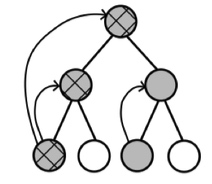
  • 在所有节点 计算 极小、极大搜索
  • 价值从搜索值备份得到，在同一个step，对所有节点

\[\begin{aligned}
v\left(s, \mathbf{w}\right) & \leftarrow v_{+}\left(s, \mathbf{w}\right) \\
\Longrightarrow v\left( s, \mathbf{w}\right) & \leftarrow v\left(l_{+}\left(s \right), \mathbf{w}\right)
\end{aligned}\]

Treestrap in chess ：meep

  • 2k个特征，二进制线性组合价值函数
  • 随机初始权重
  • 权重调节方式：Treestrap
  • 自驱动学习过程表现高效：利用率高
  • 随机权重情况下表现良好

Simulation-based Search

  • 自驱动RL 可以替代 搜索
  • 基于仿真的游戏从根节点 \(s_t\)开始
  • 应用RL 到 仿真经验
    • MC control \(\Rightarrow\) MC tree search
    • 最高效的变体算法是 UCT 算法
      • 使用置信上界UCB 来平衡探索和利用
    • 自驱动 UCT 收敛于 极小极大价值函数
    • 在完美信息游戏、不完美信息游戏均表现良好

MCTS蒙特卡洛树搜索 表现in games

简单蒙特卡洛搜索 in Maven（拼字游戏）

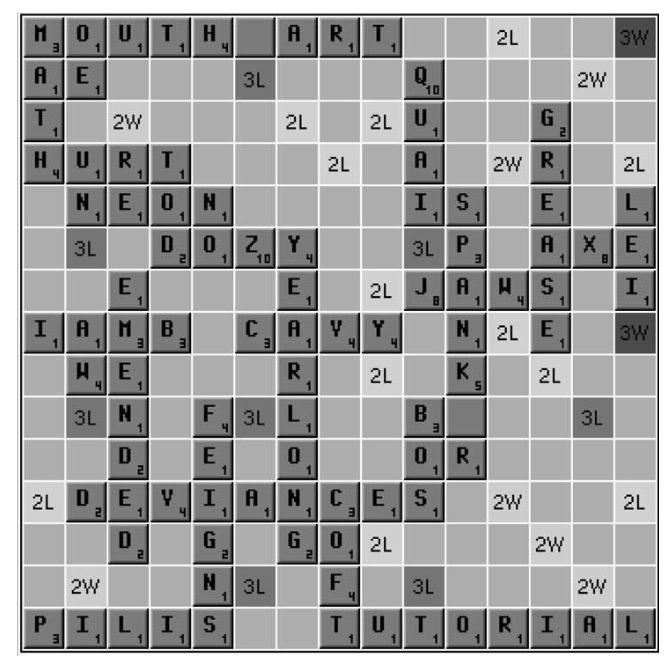
  • 学习 价值函数

    • 二进制价值函数
    • MC policy iteration

  • 搜索 价值函数，

    • 搜索n步
    • 使用学到的价值函数评价 当前状态
    • x
    • 选择高分动作
    • 特定的endgame 用\(B^*\)

6、在非完整信息中的强化学习

Game tree search 在不完美信息游戏中

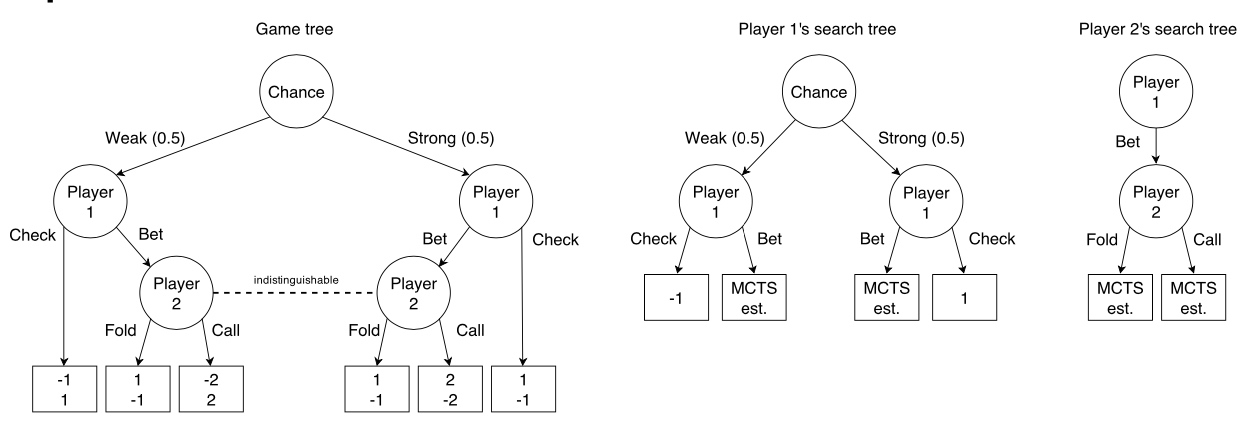
真实的状态可能共享相同的信息状态空间

Solution：

  • Iterative forward-search mehtods
    • e.g. 反事实的 后悔值最小化
  • 自驱动RL
  • e.g. smooth UCT

Smooth UCT search

  • 应用 MCTS 到 信息状态游戏树
  • UCT的变种，由博弈论的虚拟play启发
    • 代理agent根据对手的平均行为作出 动作 并 学习

  • 从节点的动作计数中 提取 平均策略
    \[\pi_{a v g}(a \mid s)=\frac{N(s, a)}{N(s)}\]

  • 对每个节点，根据UCT概率选择动作
    \[A \sim\left\{\begin{array}{ll}
    \text { UCT }(S), & \text { with probability } \eta \\
    \pi_{\text {avg}}(\cdot \mid S), & \text { with probability } 1-\eta
    \end{array}\right.\]

  • 经验

    • Naive MCTS 发散
    • Smooth UCT 收敛到纳什平衡点

7、结论

posted @ 2020-09-08 14:58  Tolshao  阅读(677)  评论(0)  编辑  收藏  举报