强化学习笔记7：策略梯度 Policy Gradient

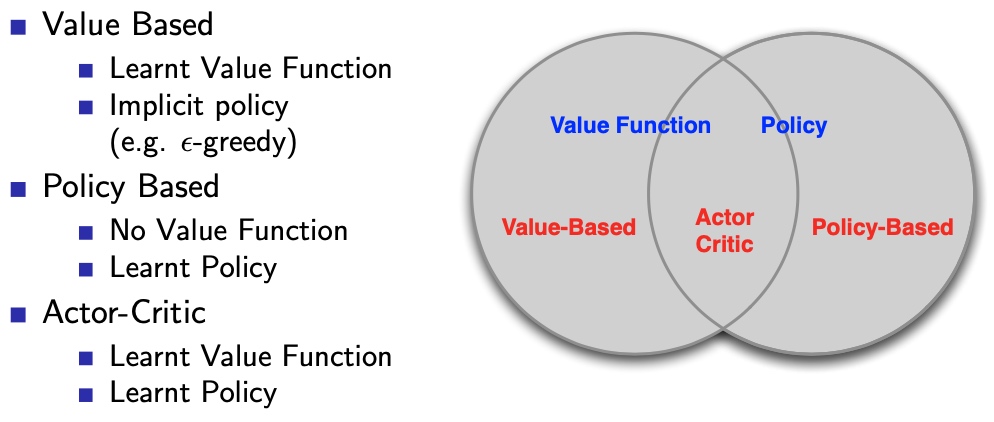
之前的策略优化，用的基本都是\(\epsilon\)-greedy的policy improve方法，这里介绍policy gradient法，不基于v、q函数

1. introduction

策略梯度是以\(P(a|s)\)入手，概率\(\pi(s,a)\)的形式，同样是model free的

\[
\pi_{\theta}(s, a)=\mathbb{P}[a \mid s, \theta]
\]
调整策略的概率分布，寻找最优策略\(\pi_*\)

特点

• 优点：
  • 更好收敛性
  • 高维、连续动作空间高效
  • 从随机策略中学习
• 缺点：
  • 会限于局部最优，而不是全局最优
  • 评价策略的过程：低效、高方差
• 随机策略有时是最优策略，基于价值函数的策略有时会限于局部最优

Policy Objective function 策略目标函数

对于不同的任务，需要建立针对性的3种目标函数

• 1.Start Value：任务有始有终
  \[
  J_{1}(\theta)=V^{\pi_{\theta}}\left(s_{1}\right)=\mathbb{E}_{\pi_{\theta}}\left[v_{1}\right]
  \]
• 2.Average Value：连续任务，不停止。对所有状态求平均，d是状态s在策略\(\pi\theta\)下的分布函数。根据V值求P
  \[
  J_{a v V}(\theta)=\sum_{s} d^{\pi_{\theta}}(s) V^{\pi_{\theta}}(s)
  \]

• 3.Average reward per time-step：连续任务，不停止。d是状态s在策略\(\pi\theta\)下的分布函数。根据R值求P
  \[
  J_{a v R}(\theta)=\sum_{s} d^{\pi_{\theta}}(s) \sum_{a} \pi_{\theta}(s, a) \mathcal{R}_{s}^{a}
  \]

• Objective：优化目标函数
  find \(\theta\) 最大化 \(J(\theta)\)

2. Finite Difference PG 有限差分策略梯度

对每个维度的权重，分别进行查分求梯度，然后迭代权重，至最优

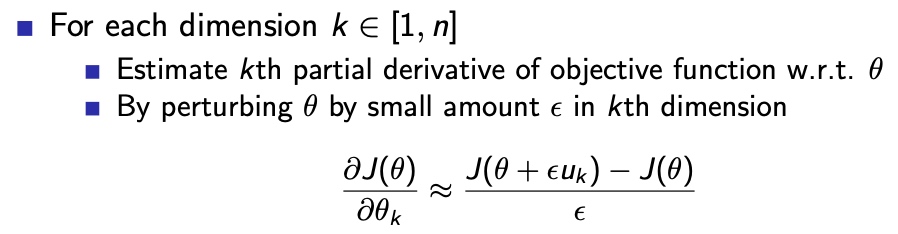
特点：

• n次运算，求得n维的梯度
• 简单、噪声、偶尔高效
• 通用性好，任意策略可用，即使策略目标函数不可微

3. MC PG 蒙特卡洛策略梯度

要求：策略目标函数可微分，梯度可计算
引入了似然比概念

Likelihood ratios

Score function（not value function）

• Trick here： 用似然比 Likelihood ratios
  将\(\pi\)梯度，变为\(\pi\) 乘以 log 的梯度
  函数在某个变量θ处的梯度等于该处函数值与该函数的对数函数在此处梯度的乘积 \(d log(y) = dy/y\)，默认底数为\(e\)
  \[
  \begin{aligned}
  \nabla_{\theta} \pi_{\theta}(s, a) &=\pi_{\theta}(s, a) \frac{\nabla_{\theta} \pi_{\theta}(s, a)}{\pi_{\theta}(s, a)} \\
  &=\pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta}(s, a)
  \end{aligned}
  \]

• Score function: \(\nabla_{\theta} \log \pi_{\theta}(s, a)\)

Softmax policy：策略概率按照指数分配

线性组合 -> softmax = \(\pi\) 是状态s下，采取每个a的概率

通过取对数，拆分为加法，进而表示为

Gaussian polisy：策略概率按照距离分配

• In continuous action spaces, a Gaussian policy is natural
• Mean is a linear combination of state features \(μ(s) = φ(s)^{T}θ\)
• Variance may be fixed σ , or can also parametrised Policy is Gaussian, a ∼ N (μ(s), σ2)
• The score function is
  \[
  \nabla_{\theta} \log \pi_{\theta}(s, a)=\frac{(a-\mu(s)) \phi(s)}{\sigma^{2}}
  \]

在实际应用中，要注意梯度消失现象，可以利用代数方法求解

Policy Gradient theorem 策略梯度定理

One-step MDPs

没有序列，整个任务过程只有一步

• 状态s~d(s)
• r = R_{s,a}

用似然比，计算策略梯度：
先给出奖励函数，三种形式一样如下：
\[
\begin{aligned}
J(\theta) &=\mathbb{E}_{\pi_{\theta}}[r] \\
&=\sum_{s \in \mathcal{S}} d(s) \sum_{a \in \mathcal{A}} \pi_{\theta}(s, a) \mathcal{R}_{s, a} \\
\end{aligned}\]

相应梯度表示为：
\[
\begin{aligned}
\nabla_{\theta} J(\theta) &=\sum_{s \in \mathcal{S}} d(s) \sum_{a \in \mathcal{A}} \pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta}(s, a) \mathcal{R}_{s, a} \\
&=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) r\right]
\end{aligned}
\]

对于多步的标准MDPs

用Q函数，替代R函数，即可表征序列到End的奖励
对于下列都适用：

• 初始价值函数：\(J = J_1\)
• 平均奖励函数： \(J_{avR}\)
• 平均价值函数： \(\frac{1}{1-\gamma}J_{avV}\)

对任意可微策略，梯度都为
\[
\nabla_{\theta} J(\theta)=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) Q^{\pi_{\theta}}(s, a)\right]
\]

MCPG 蒙特卡洛策略梯度法

• 采样 替代 期望
  上节式子表示为Score function 和 Q 值在策略\(\pi\)下的期望
  在MC中，在每个episode在\(\pi\)下，产生的序列就满足分布，整个过程都迭代完后的值，自然就是期望，因此梯度前没有概率分布函数，用常值替代。

• 特点：
  • 动作平滑
  • 收敛性好，但是慢
  • 方差大

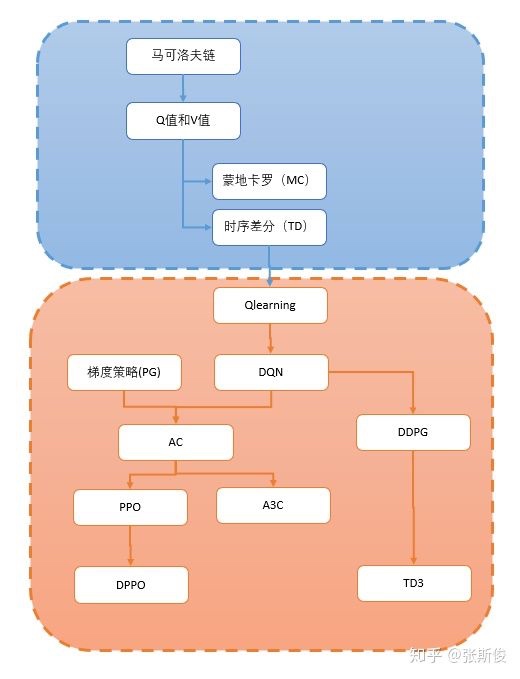
4. Actor-Critic PG AC策略梯度

ACPG提出，解决PG方差大的问题
为了加快更新速度，我们希望把回合更新变为，每步更新，需要Q的估计值（指导策略更新），引入函数逼近器，取代PG中的Q采样
\[
Q_W(s,a) \approx Q^{\pi \theta}(s,a)
\]
AC算法的主要部分

• Critic：用来估计价值函数，（更新q(s,a,w)的参数w）
• Actor：生成动作，（在critic的指引下，更新\(\pi_\theta\)的参数\(\theta\)）

AC算法遵循， 近似策略梯度法
\[
\begin{aligned}
\nabla_{\theta} J(\theta) & \approx \mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) Q_{w}(s, a)\right] \\
\Delta \theta &=\alpha \nabla_{\theta} \log \pi_{\theta}(s, a) Q_{w}(s, a)
\end{aligned}
\]

例子：简单线性价值函数的AC算法

• Critic 线性组合，TD(0)
• Actor PG更新

• 逐步更新，在线实时
  

• AC算法中的偏差

  • 对PG的估计引入了偏差
  • 正确选择价值函数，有利于减小、消灭偏差，but how？？？

Compatible function approximation 兼容函数估计

上节线性近似的价值函数引入了偏差，小心设计的Q函数满足：

1.近似价值函数的梯度完全等同于策略函数对数的梯度，即不存在重名情况：
\[
\nabla_{w} Q_{w}(s, a)=\nabla_{\theta} \log \pi_{\theta}(s, a)
\]
2.价值函数参数w使得均方差最小：
\[
\varepsilon=\mathbb{E}_{\pi_{\theta}}\left[\left(Q^{\pi_{\theta}}(s, a)-Q_{w}(s, a)\right)^{2}\right]
\]
此时策略梯度是准确的，满足
\[
\nabla_{\theta} J(\theta)=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) Q_{w}(s, a)\right]
\]

• 证明过程，（参数梯度 = 0）

Tricks——Advantage function critic

核心思想：减去一个baseline，将MSE的减数和被减数都 往 0 方向拉，减小偏差
Advantage function = PG减去B(s)，好的B(s)是状态价值函数，V(s)是和策略无关的值，所以不改变梯度的期望的值

实现方法

• 通过两个估计函数 和 两套参数，分别估计V、Q，进而估计A
  

• 直接用v值运算
  但是并不需要用2个估计函数，因为TD误差是Q-V的无偏估计

不同时间尺度下——Eligibility Traces

几种时间尺度下的更新算法

• 针对Critic过程使用TD(λ)
  

• 针对Actor过程使用TD(λ)
  

将TD(λ)的后向视角算法应用于实际问题时，可以在线实时更新，而且不需要完整的Episode。

PG是理论上是基于真实价值函数V(s)的
但是critic给PG提供了V的估计值，进而PG用估计的梯度去更新参数θ
结论是梯度也能使Actor更新到最优策略\(\pi\)

Natural policy gradient

高斯策略：按照期望和概率执行动作
缺点：对梯度估计不利，收敛性不好

Solution：Natural PG

• 参数化独立

• 估计值与真值近似

• 对目标函数改写（噪声为0下）
  \[
  \nabla_{\theta}^{\text {nat}} \pi_{\theta}(s, a)=G_{\theta}^{-1} \nabla_{\theta} \pi_{\theta}(s, a)
  \]

• Fisher information matrix 费雪信息矩阵
  G反应了对估计值的准确程度，值越大，梯度更新越小，抑制噪声
  \[
  G_{\theta}=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta}(s, a)^{T}\right]
  \]

• Compatible function approximation
  \[
  \nabla_{w} A_{w}(s, a)=\nabla_{\theta} \log \pi_{\theta}(s, a)
  \]

• 简化为
  \[
  \begin{aligned}
  \nabla_{\theta} J(\theta) &=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) A^{\pi_{\theta}}(s, a)\right] \\
  &=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta}(s, a)^{T} w\right] \\
  &=G_{\theta} w \\
  \nabla_{\theta}^{n a t} J(\theta) &=w
  \end{aligned}
  \]

• 用Critic参数，更新Actor参数

总结PG