强化学习笔记5:无模型控制 Model-free control
适用于:
- MDP model 未知:经验的采样可以获取
- MDP model 已知:无法使用(e.g.原子级动力学),采样可以使用
策略、非策略学习:
- On-policy:动作采样来自policy \(\pi\)
- Off-policy:采样来自采样μ 或 来自于其他策略\(\pi\),
On-policy MC control
贪婪策略梯度法如果用V(s),需要MDP已知
对于已知MDP,可以通过策略迭代的方法,DP到最优策略
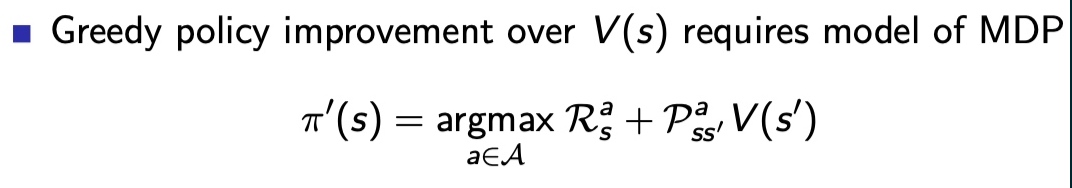
要实现不基于模型的控制,需要满足两个条件:
- 引入q(s,a)函数,而不是v(s)
- 探索,避免局部最优,引入\(\epsilon\),使\(\pi\)以小概率随机选择剩余动作,避免每次都选择已知较优动作
model-free policy using action-value function
用Q(s,a),不需要已知MDP

每个箭头对应一个段,Prediction一次,Control一次
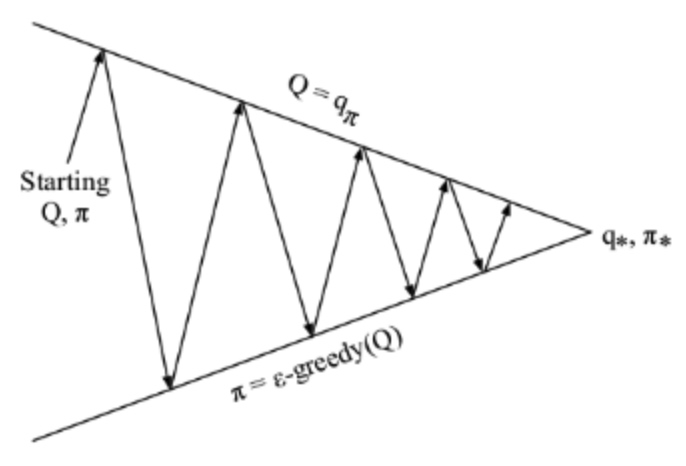
GLIE MC control(Greedy in the Limit with Infinite Exploration)
保证试验进行一定次数是,所有a-s状态都被访问到很多次

随实验次数进行,减小\(\epsilon\)值

ON-policy TD learning
- TD与MC control 区别,希望引入TD的特性到on-policy learning

Sasra
Sasra(one-step)
由贝尔曼公式推导
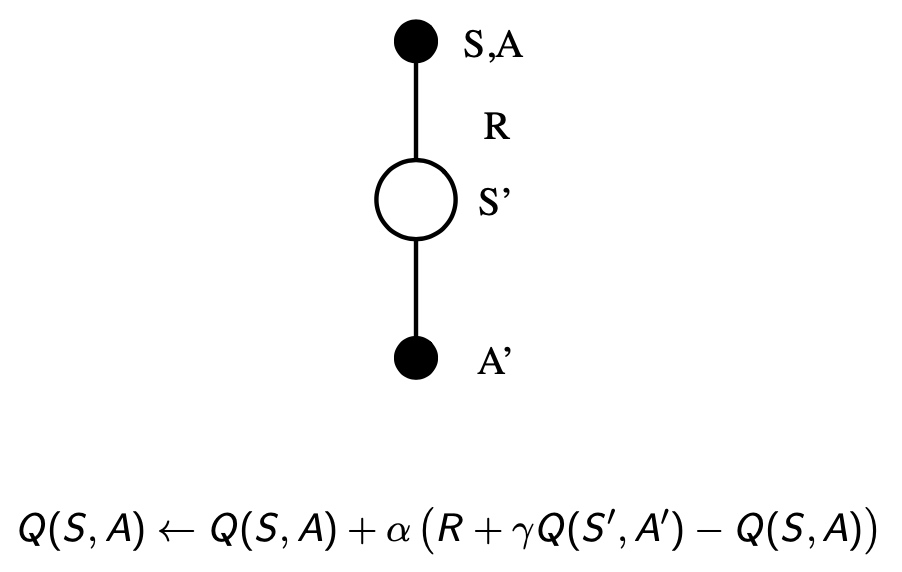
算法实现过程

要保证Q值收敛,需要服从下列2个条件
- 策略符合GLIE特性
- 计算步长满足如图:

n-step Sarsa
与TD(λ)类似,扩展q的视野

Forward view Sarsa(λ)
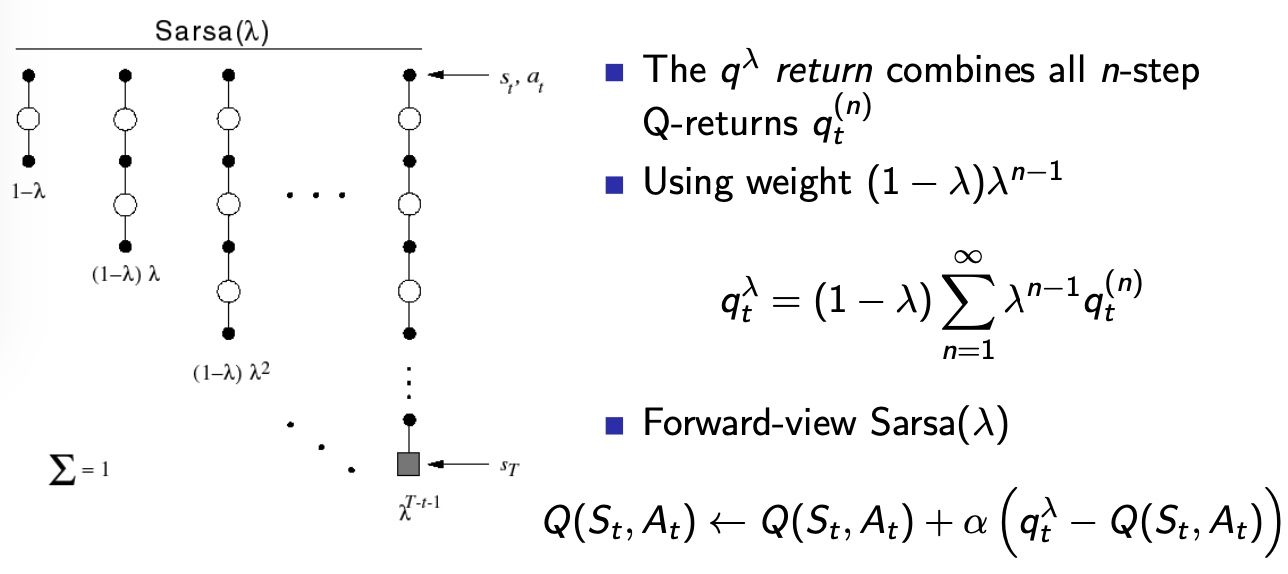
Backward view Sarsa(λ)
在正向视角中,迭代一次Q值,需要完整的一次episode
为了解决这个问题,引入迹的概念,实现incremental update

算法流程

Attention:迹E是属于episode的,切换episode后,E要归零
Off-policy learning
需求
- 从人类和其他agents的表现中学习
- 从old policies \(\pi_1, \pi_2...\)中学习
- 从随机策略中,学习到最优策略
- 从一个策略中,学习到多个策略
采样不同分布
\[
\begin{aligned}
\mathbb{E}_{X \sim P}[f(X)] &=\sum P(X) f(X) \\
&=\sum Q(X) \frac{P(X)}{Q(X)} f(X) \\
&=\mathbb{E}_{X \sim Q}\left[\frac{P(X)}{Q(X)} f(X)\right]
\end{aligned}
\]
off-policy MC learning
引入了概率缩放系数,判断两个策略动作概率函数

- 缺点:
- 方差会增加
- \(\mu =0\)无法计算
off-policy TD learning
利用期望分布的概念,在更新目标前x一个系数,对当前策略的置信度
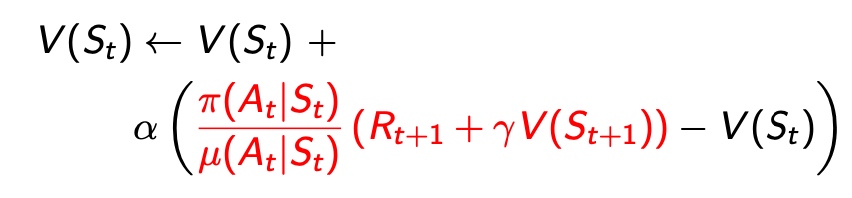
- 优点:
- 低方差
- 单步策略需要相似
Q-learning
特点
- 采用Q(s,a) instead of V(s)
- 不需要重要性采样 系数
- 下次动作用 \(A_{t+1} ∼ μ(·|S_t)\)
- 动作服从策略 as \(A′ ∼ π(·|S_t)\)
更新方程如下
\[
Q\left(S_{t}, A_{t}\right) \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left(R_{t+1}+\gamma Q\left(S_{t+1}, A^{\prime}\right)-Q\left(S_{t}, A_{t}\right)\right)
\]
off-policy control with Q-learning
在学习过程中:
- Q值的Update Target 被优化,target policies是\(\epsilon-greedy\)的
- Actor 执行的策略\(\pi\)被优化,执行\(\epsilon-greedy\)
采用下式更新策略:
\[
\pi\left(S_{t+1}\right)=\underset{a^{\prime}}{\operatorname{argmax}} Q\left(S_{t+1}, a^{\prime}\right)
\]
Q-learning target 简化为:
\[
\begin{aligned}
& R_{t+1}+\gamma Q\left(S_{t+1}, A^{\prime}\right) \\
=& R_{t+1}+\gamma Q\left(S_{t+1}, \underset{a^{\prime}}{\operatorname{argmax}} Q\left(S_{t+1}, a^{\prime}\right)\right) \\
=& R_{t+1}+\max _{a^{\prime}} \gamma Q\left(S_{t+1}, a^{\prime}\right)
\end{aligned}
\]
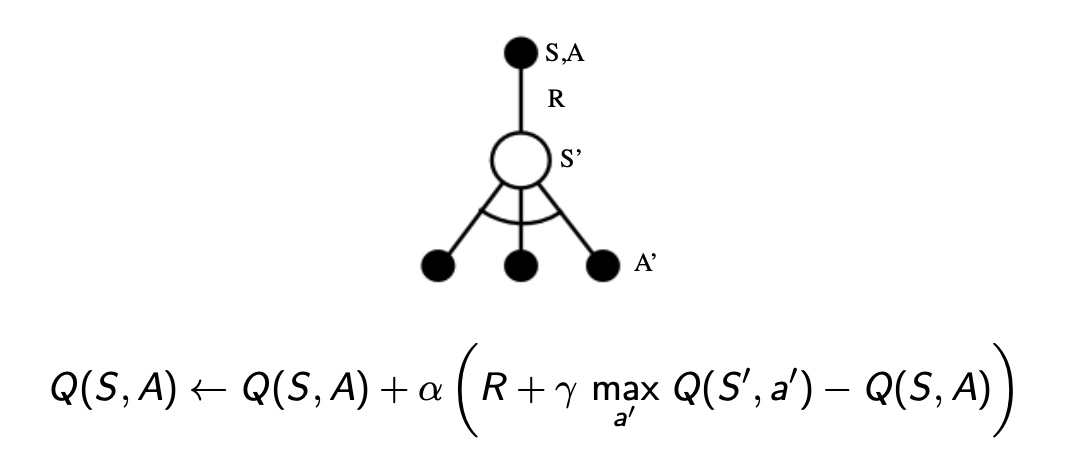
迭代使\(Q(s,a) \rightarrow q_* (s,a)\)
Attention:在迭代过程中,动作采用\(\epsilon-greedy\)策略,保证对位置环境的探索
算法流程
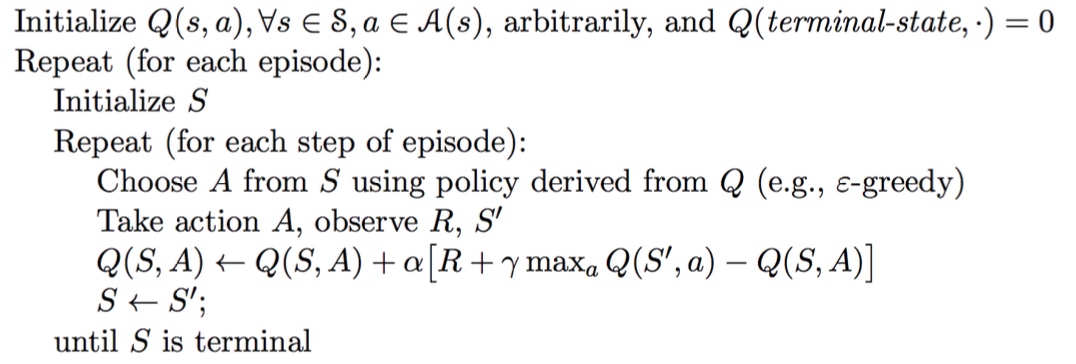
总结
DP TD的关系
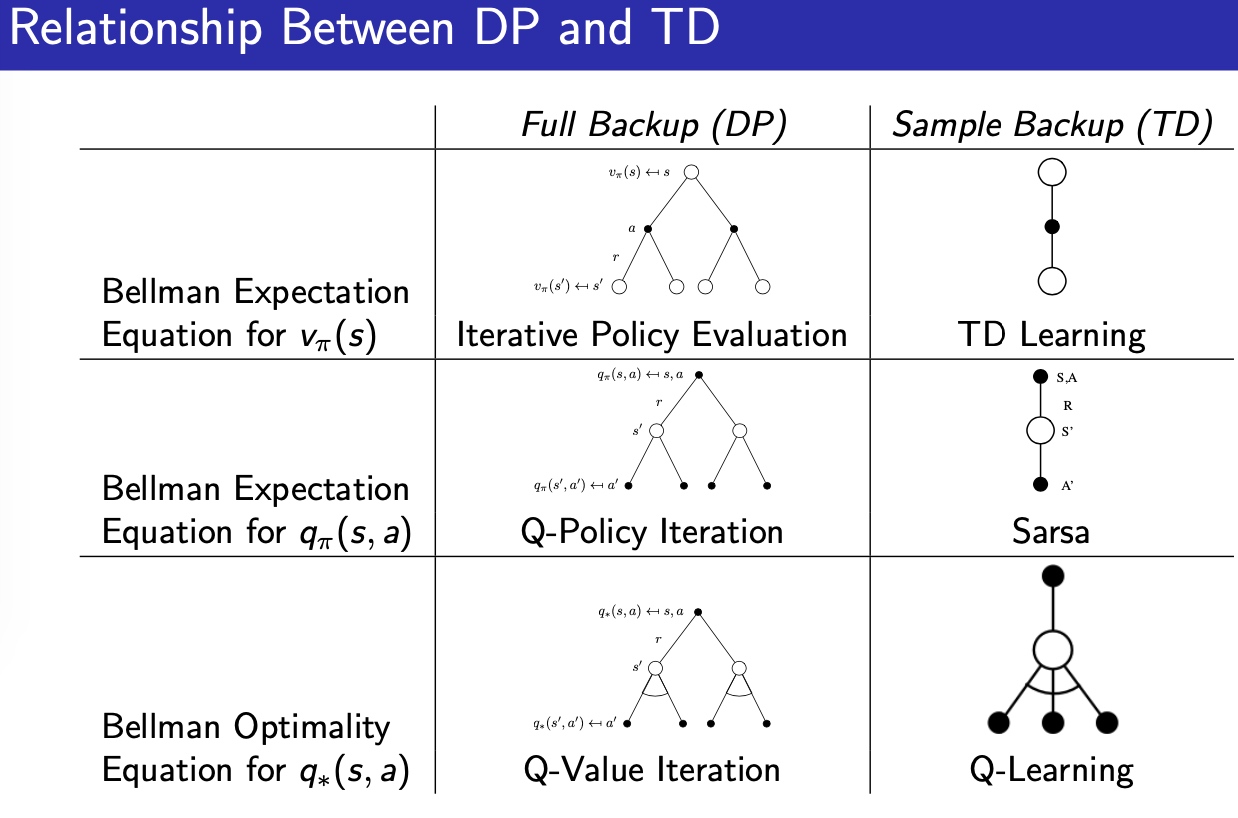

Q-learning 和 SARSA区别
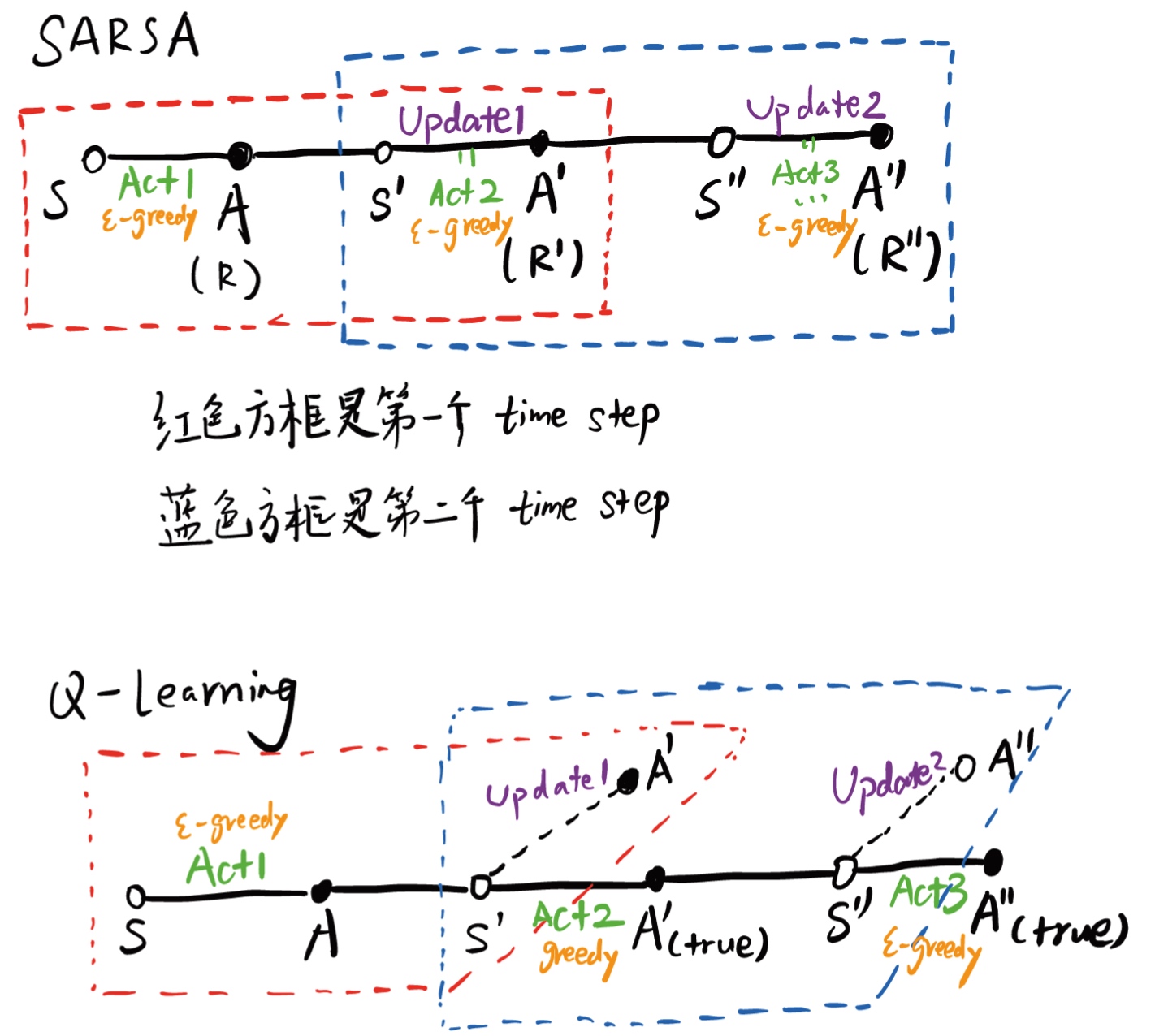
区别在于:
Q-learning:
- update: \(greedy\)策略,评估过程的A'没有实际执行
- control:\(\epsilon-greedy\)策略
SARSA:更新和执行都用\(\epsilon-greedy\)策略