强化学习笔记4:无模型预测 model-free prediction
Introduction
这一章,解决的是用prediction的方法,来评估策略\(\pi\)的问题。
对于Env来说,不是参数已知的MDP
比如元组中a、s、P的关系不确定 or 未知
Prediction -> Control
Evaluation -> Optimization
蒙特卡洛法 Monte-Carlo learning
- 定义:在不清楚MDP状态转移及即时奖励的情况下,直接从经历完整的Episode来学习状态价值,通常情况下某状态的价值等于在多个Episode中以该状态算得到的所有收获的平均。
适用于MDP参数未知,回合制更新,遍历了所有状态s
MC是基于大数定律的:
当采样足够多时,就可以代表真值
\[ N(s)->\infty \Rightarrow V(s) -> V_\pi(s)\]
- 说明:
- 均值累计计算可以用\(v = sum/N\)
- 也可以用累进更新 Incremental Mean
\[
\begin{aligned}
\mu_{k} &=\frac{1}{k} \sum_{j=1}^{k} x_{j} \\
&=\frac{1}{k}\left(x_{k}+\sum_{j=1}^{k-1} x_{j}\right) \\
&=\frac{1}{k}\left(x_{k}+(k-1) \mu_{k-1}\right) \\
&=\mu_{k-1}+\frac{1}{k}\left(x_{k}-\mu_{k-1}\right)
\end{aligned}
\]
类似于PID的P 增益随着N增大,在逐步缩小
为了简化计算,改写方程,用\(\alpha\)代替\(\frac{1}{N(s_t)}\)
这样可以用固定步长来替代变步长\(\frac{1}{k}\)
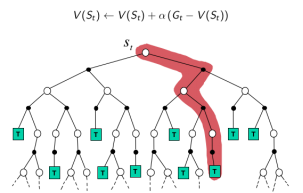
\[V(S_t) \leftarrow V(S_t)+\alpha(G_t - V(S_t))\]
可以看做是,\(v_{new} = v_{old} + \alpha(v_{target} - v_{old})\),括号里面是误差
可以看到这里的\(\alpha\)和机器学习里面用的学习率是一个符号
差分法Temporal-Difference learning
MC 在 episode遍历完之后,回合更新,效率低
TD 实现边走边更新
引入时间t的概念
- 直接从episodes 的经验学习
- model-free:不知道MDP的Transition转移和Reward回报
- Bootstrapping自举学习,从部分例子学习
Goal:学习\(v_{\pi}\) 的值,under policy \(\pi\)
时序分析法 TD(0):
\[
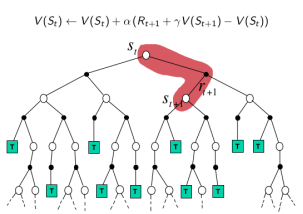
V\left(S_{t}\right) \leftarrow V\left(S_{t}\right)+\alpha\left(R_{t+1}+\gamma V\left(S_{t+1}\right)-V\left(S_{t}\right)\right)
\]
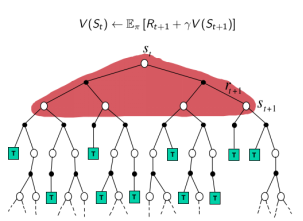
- TD target 是 下一个时刻的\(R_{t+1}+\gamma V\left(S_{t+1}\right)\)
- TD误差:\(\left(R_{t+1}+\gamma V\left(S_{t+1}\right)-V\left(S_{t}\right)\right)\)
Bootstrapping:根据episode表现来更新V值,自举(依靠自己努力获得)
与MC方法区别
| 项目 | MC | TD |
|---|---|---|
| 不完整片段学习能力 | 无 | 有 |
| 在线学习(every step)能力 | update until the end | 有 |
| loop环境学习能力 | 无,必须terminating | 有 |
| 收敛性好 | 是 | |
| 初值敏感 | 否 | 是 |
| 偏差bias | zero | some |
| 方差variance | high | low |
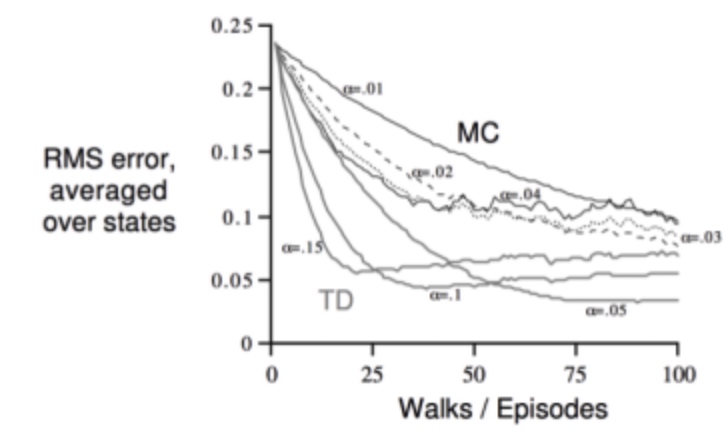
估计方法背后的理论
- MC方法:最小化均方根MSE
\[
\sum_{k=1}^{K} \sum_{t=1}^{T_{k}}\left(G_{t}^{k}-V\left(s_{t}^{k}\right)\right)^{2}
\] - TD(0)方法:最大似然估计 max likelihood Markov model
Solution to the MDP \(\langle\mathcal{S}, \mathcal{A}, \hat{\mathcal{P}}, \hat{\mathcal{R}}, \gamma\rangle\) that best fits the data
\[
\hat{\mathcal{P}}_{s, s^{\prime}}^{a} =\frac{1}{N(s, a)} \sum_{k=1}^{K} \sum_{t=1}^{T_{k}} 1\left(s_{t}^{k}, a_{t}^{k}, s_{t+1}^{k}=s, a, s^{\prime}\right)
\]
\[
\hat{\mathcal{R}}_{s}^{a} =\frac{1}{N(s, a)} \sum_{k=1}^{K} \sum_{t=1}^{T_{k}} 1\left(s_{t}^{k}, a_{t}^{k}=s, a\right) r_{t}^{k}
\]
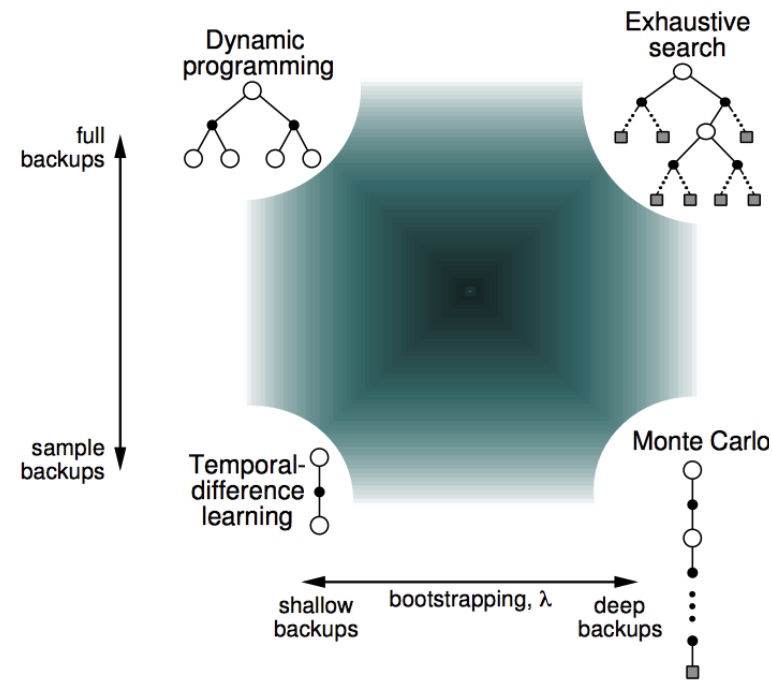
总结:DP、MC、TD
- Bootstrapping自举:利用自己估计值update
- Sampling采样 :更新样本期望
| 项目 | 动态规划DP | 蒙特卡洛MC | 差分TD |
|---|---|---|---|
| 自举Bootstrapping | 1 | 0 | 1 |
| 采样Sampling | 0 | 1 | 1 |
- TD用了Markov特性,因此在MP过程高效
- MC相反,统计规律,非MP过程同样有效
MC: 采样,一次完整经历,用实际收获更新状态预估价值
TD:采样,经历可不完整,用喜爱状态的预估状态价值预估收获再更新预估价值
DP:没有采样,根据完整模型,依靠预估数据更新状态价值
TD(λ)法
视野(深度)影响TD算法的稳定性,但是视野去多深,不知道
因此,综合不同深度的视野,加权求和,即TD\((\lambda)\)
扩展TD(0),视野扩展到N个step,N=全过程时,变为MC
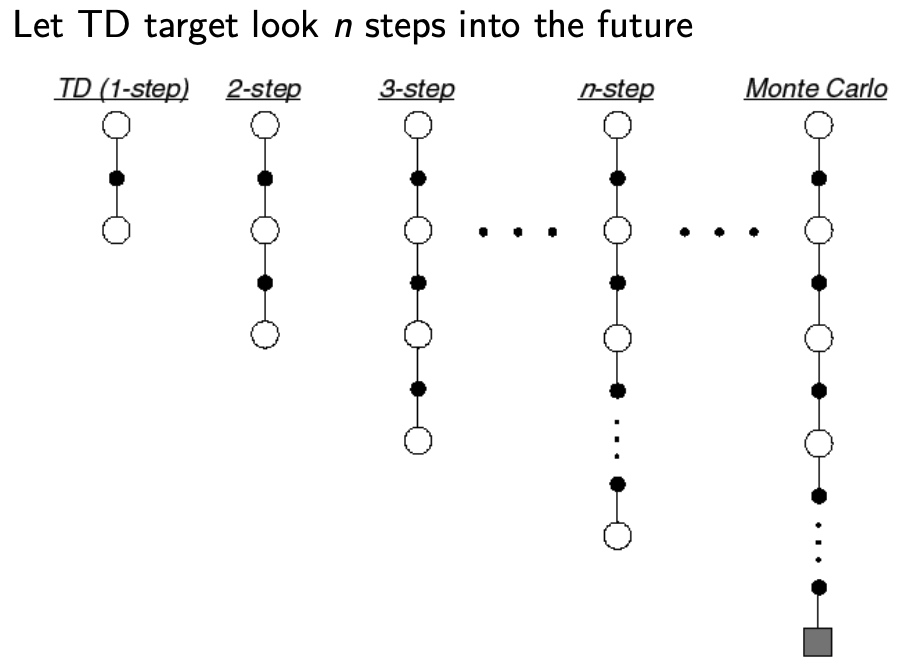
TD(N)推导

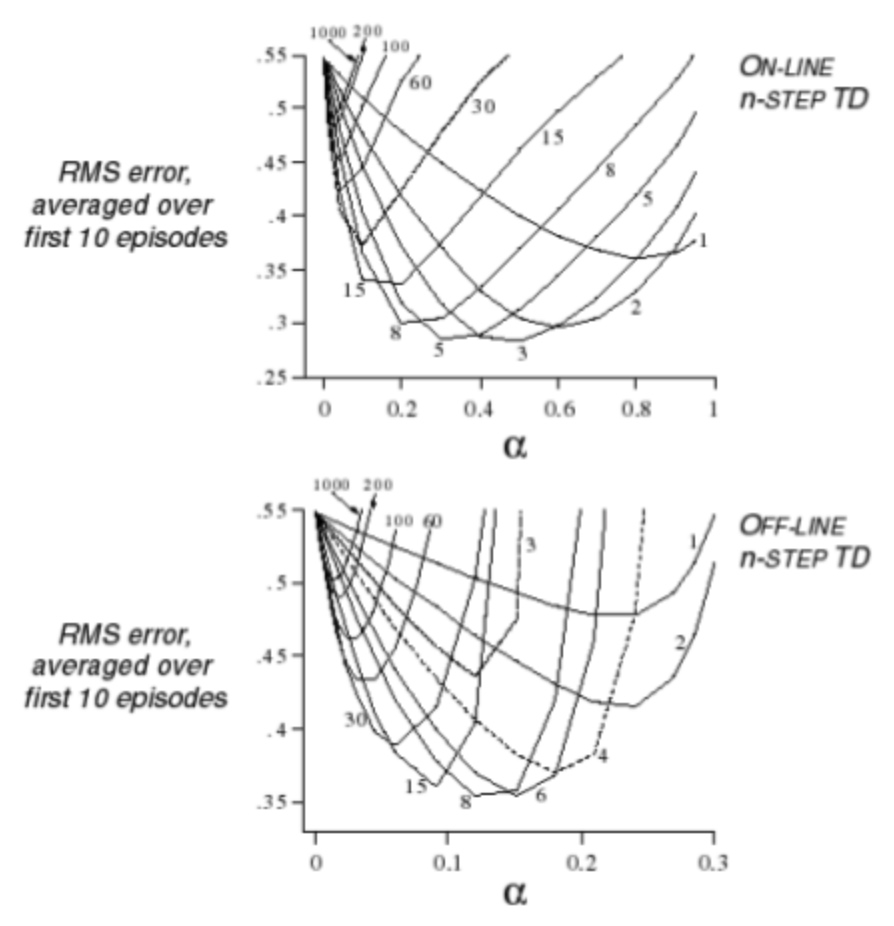
对于某个问题来说,没有那个N值是最优的
因此,用几何加权的方法来对视野做平均
Forward 前向视角认知 \(TD(\lambda)\)
例子:
老鼠在连续接受了3次响铃和1次亮灯信号后遭到了电击,那么在分析遭电击的原因时,到底是响铃的因素较重要还是亮灯的因素更重要呢?

两个启发:
- 出现频率高的状态
- 出现频率低的状态
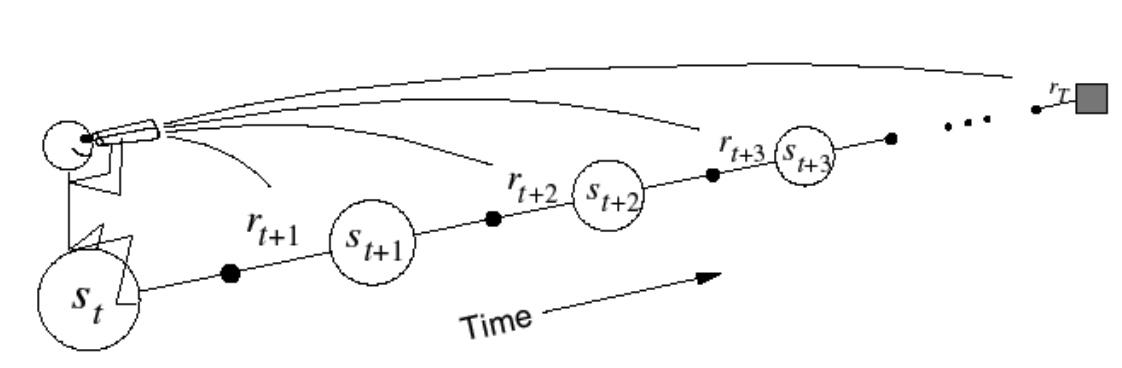
\(\lambda\):对视野的平均
for iteration: t -> t+1
update value function

引入权重概念,前面的重要,指数衰减
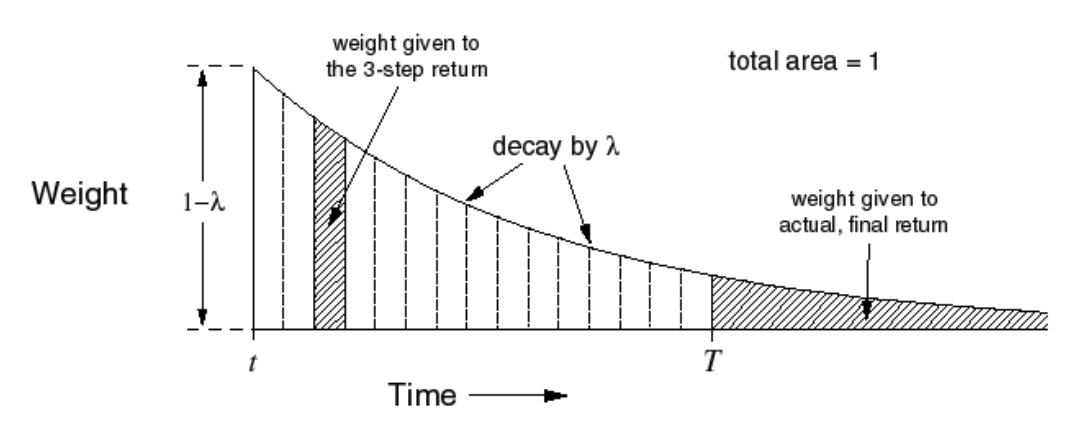
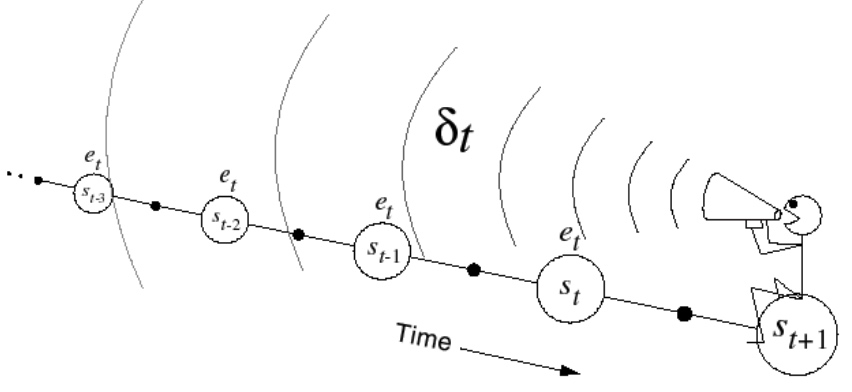
Backward 反向认知TD(λ):提供了单步更新的机制
Credit assignment:
引入 Eligibility Traces:状态s的权重,是一个时间序列
当s重复出现,E值升高,不出现,指数下降
\(E_{0}(s)=0\)
\(E_{t}(s)=\gamma \lambda E_{t-1}(s)+\mathbf{1}\left(S_{t}=s\right)\)
Backward步骤:
- 对每个状态s 创建 迹值
- 对每个状态s 更新 V(s)
- 与 TD-error(\(\delta_t\)) 和 Eligibility trace \(E_t(s)\) 成比例
\[
\begin{aligned}
\delta_{t} &=R_{t+1}+\gamma V\left(S_{t+1}\right)-V\left(S_{t}\right)\\
V(s) & \leftarrow V(s)+\alpha \delta_{t} E_{t}(s)
\end{aligned}
\]
\[
\sum_{t=1}^{T} \alpha \delta_{t} E_{t}(s)=\sum_{t=1}^{T} \alpha\left(G_{t}^{\lambda}-V\left(S_{t}\right)\right) 1\left(S_{t}=s\right)
\]

总结
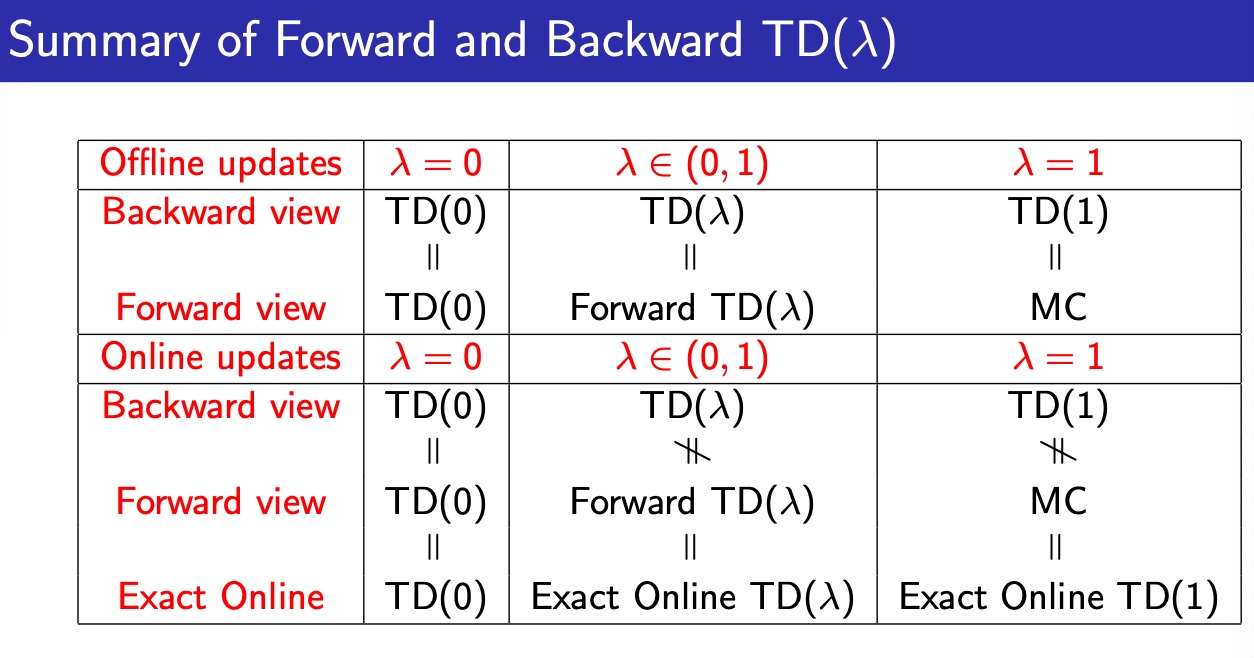
- Offline update:TD(0) = TD(\(\lambda\)) = TD(1)
- Online update: TD(\(\lambda\))前后向视图不一致,引入Exact online TD(\(\lambda\))可以解决这个问题
- TD(0) 向后看一步
- TD(\(\lambda\)) 视野距离按\(\lambda\)指数衰减,叠加
- TD(1) 视野不按指数衰减
- 能在RL中被应用,看中了TD的自举特性