强化学习笔记3：动态规划 planning by dynamic programming（DP）

规划，适用于MDP模型参数已知
学习，适用于Env未知或部分未知

概述

动态规划分为两步，Prediction、Control

• （Prediction）Value:是对策略\(\pi\)的评价
  \[<s,P^\pi,R^\pi,\gamma>, \pi \rightarrow V_\pi\]
• （Control）Policy \(\pi\):是对Value的选择
  \[<s,P^\pi,R^\pi,\gamma>, V \rightarrow \pi \]

方法：

• prediction：迭代法
  对所有状态s，应用贝尔曼公式
  \[
  v_{k+1}(s)=\sum_{a \in A} \pi(a \mid s)\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{k}\left(s^{\prime}\right)\right)
  \]

右边的\(v_k\)不确定，但是迭代下去，因为\(R^a_s\)确定，所以收敛到真值\(v_\pi\)

• Control：greedly，每次都选基于上次预测最好的那个a

例子

问题：每走一步，r = -1，走到出口可以停止
在随机策略下，迭代k，最使v收敛
得到\(v^{\pi}(s)\)

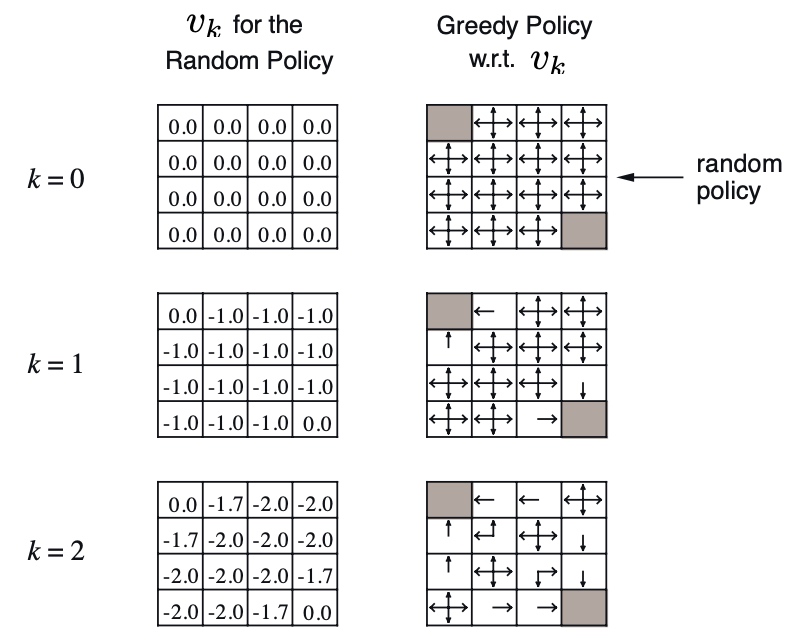
然后最简单的策略，greedy，往v值高的地方走。

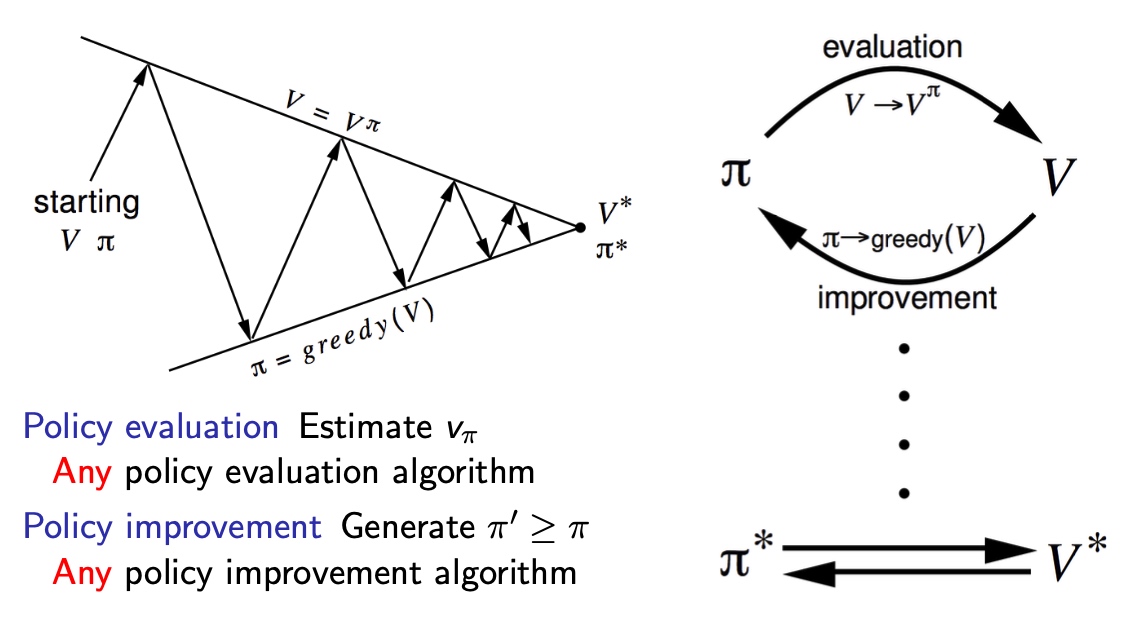
Policy iteration：\(O(mn^2)\)

每一步，遍历动作A

Find optim policy：
以Greedy为例，迭代：\(\pi' = greedy(v_{\pi})\)
策略更新为：
\[
\pi^{\prime}(s)=\underset{a \in \mathcal{A}}{\operatorname{argmax}} q_{\pi}(s, a)
\]
值函数更新为：
\[
v_{\pi}(s)=\max _{a \in \mathcal{A}} q_{\pi}(s, a)
\]
主动改变策略，策略改变之后进行评估
根据q值，从集合A中选a，更新策略\(\pi\)，使新q大于之前一步
\[
q_{\pi}\left(s, \pi^{\prime}(s)\right)=\max _{a \in \mathcal{A}} q_{\pi}(s, a) \geq q_{\pi}(s, \pi(s))=v_{\pi}(s)
\]

证明：
\[
\begin{aligned}
v_{\pi}(s) & \leq q_{\pi}\left(s, \pi^{\prime}(s)\right)=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] \\
& \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, \pi^{\prime}\left(S_{t+1}\right)\right) \mid S_{t}=s\right] \\
& \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} q_{\pi}\left(S_{t+2}, \pi^{\prime}\left(S_{t+2}\right)\right) \mid S_{t}=s\right] \\
& \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\ldots \mid S_{t}=s\right]=v_{\pi^{\prime}}(s)
\end{aligned}
\]
所以保证了每次迭代，价值函数 与 策略 增长

Value iteration：\(O(m^2n^2)\)

每一步，遍历了状态S和动作A

最优策略：

• 当前状态s下，所有动作a产生回报的最大值
• 采取动作a后，状态由s -> s'的期望
  公式：
  \[
  v_{*}(s)=\max _{a} \mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{*}\left(s^{\prime}\right)
  \]

根据值函数，选择策略

值迭代和policy迭代的区别

• policy iteration每次迭代v(s)都会变大；而value iteration则不是。
• 价值迭代不需要策略参与，依据MDP 模型，直接迭代，需要P矩阵、r 等已知
  • policy iteration： policy->value->policy
  • value iteration：value->value

Trick:

三种值迭代方法:
常规的值迭代，要遍历过所有s之后，才进行一次迭代，因此存在old、new两个v(s)

• in-place DP：新值直接替换旧值，只存储一个v(s)，
  • 异步更新，提高效率
  • 缺点：更新顺序影响收敛性
• Prioritised sweeping：state的影响力排序
  • 比较贝尔曼误差绝对值，大的更新，小的忽略
• Real-time DP：遍历过的才更新
  • 省去了agent 未遍历的状态s，对于稀疏任务效率提升极大