机器学习-Coursera笔记

AI->机器学习分类图

矩阵补课

特征值分解EVD，奇异值分解SVD

\(A\)是矩阵
\(x_i\) 是单位特征向量
\(\lambda_i\)是特征值
\(\Lambda\) 是矩阵特征值

EVD特征值分解（The eigenvalue value decomposition）

针对方阵，特征值

\(A = U\Lambda U^{-1} = U\Lambda U^T\)
进行矩阵运算时，Ax，先对x分解\(x =aU^T= a_1 x_1+...a_mx_m\)

则\(U\Lambda U^T x = U\Lambda U^T U a^T = U\Lambda a^T\)

\(U\Lambda a^T = U(\lambda a)^T\)

效果如下，将向量在单位特征向量上，伸长为\(\lambda\)倍

SVD奇异值分解（Singularly Valuable Decomposition）

矩阵A，mxn维，将n维的向量映射到m维空间中,k<=m
正交基，\((v_1,v_2...v_n)\)

\(A^T A = \lambda_j\)

应用

存储领域，选取u，v正交基矩阵，计算奇异值矩阵，使奇异值矩阵尽量集中，即可取到

机器学习

1、Introduction

E：经验
T：任务
P：概率

机器学习分类

• 监督学习(supervisor learning)：分类（classification）、回归（regression）
• 无监督学习(unsupervisor learning)：
• 强化学习Reinforcement learning

2、Linear regression线型回归

Cost funciton-代价函数

矩阵表达
\(J(\theta) = \frac{1}{2m}(X\theta-Y)^T(X\theta-Y)\)

• 梯度下降法（Gradient Descent）
  \(\theta_{i+1} =\theta_i - \alpha\nabla J(\theta) \)
  \(\frac{\partial J(\theta)}{\partial\theta} = \frac{1}{m}X^T(X\theta-Y)\)
  推导过程
  
  

• 正规方程法（Normal Equation）
  
  图中公式，theta的维是n，不是m
  另一种理解方式
  相当于求解\(Y = X\theta\)
  

b相当于y，a相当于x组成的矩阵，

求导过程

线性代数回顾

矩阵、向量使用规范

加速梯度下降方法，让\(x_i\)尺度一致

• Feature Scaling
  将输入值归一化，缩放到[-1,1]之间，梯度下降法更快收敛
• Mean Normalization
  \(x_i = \frac{x_i - \mu_i}{s_i}\),其中\(\mu_i\)是input的平均值，\(s_i\)是取值的范围，或者标准偏差

回归问题方法选择

正规方程法行不通：

• \(X^TX\)不可逆
• 元素中有redundant features,linearly dependent
• 过多的features，导致input维度n>m

回归问题的矩阵表达

3、Logistic Regression逻辑回归

分类classification

函数表达式

\(z = \theta^T x\)
\(h(z) = sigmoid(z)\)
处理regression函数：连续变离散->Hypothesis

作用

h(z)代表着一个边界，将值分为>0和<0
由于sigmoid函数的特性，程序最终会优化到z取值远离零点

Cost function 的选择

不能选择最小二乘法，因为目标是一个非凸函数
凸函数才能最好利用梯度下降法
所以对于，y-0，1的分类问题，改写cost function为

进一步改写为一个式子

推导过程中，利用了sigmoid的求导法则
\(\sigma'(x) = \sigma(x)(1-\sigma(x))\)

特殊设计过的sigmoid函数 和 cost function
使得，满足\(\theta\)参数更新可以矢量化
\(\theta_{i+1} = \theta_i - \alpha \nabla J(\theta)=\theta_i - \alpha X^T(g(X\theta) - Y)\)
\(g(X\theta)\)是sigmoid函数对\(\X\theta\)矩阵每个元素进行操作
特征缩放，

其他参数优化方法

• Conjugate gradient 共轭下降法
• BFGS
• L_BFGS
  优点：
• 不需要选择学习速率\(\alpha\)
• 收敛速度快
  缺点：复杂
  可以直接调用

1.设置优化参数 optimset = 初始参数，方法，强制结束迭代次数
2.设置初始条件，Initialpara = 
3.[Jval, theta'] = Cost_function (X,Y)
4.调用优化函数[Jval，theta'] = (@Cost_function,Initialpara,optimset)，

多类别分类

构建i个分类器，利用i个h(z)，处理
分别给出属于某个分类的几率值

X 特征矩阵

3.2回归遇到的问题，解决方案，正则化

• 过拟合
  拟合特征数>>样本量，

• 欠拟合
  特征数不够<<样本量，不能正确预测，回归

  办法

  1、 减少无关特征

• 手动减少无关特征

• 模型选择算法，自动选择相关变量
  2、 regularization 正则化
  
  正则化参数，使特征拟合参数减小权重

线性回归正则化

对于逻辑回归正则化，式子一样

4、神经网络——Nonlinear Hypotheses

输入层、隐藏层、输出层
g 激活函数\(\in[0,1]\)：
h 输出函数

• 阶跃
• 逻辑函数，sigmoid，无限可微
• 斜坡函数
• 高斯函数 ### multiclass classification
  输出层y不是一个数字，[1;0;0;0] [0;1;0;0]instead
  ### Forward propagation
  \(a^{(j+1)} = g(\Theta ^ {(j})a^{(j)})\)

Backpropagation

Cost function
符号约定

传播计算推导

BP神经网络——算法步骤

调用函数的时候 unroll矩阵->Vector

gradient check
引入 \(\epsilon\)，数值计算，缺点太慢，只用于编程时的校验

\(\Theta\)初始化
随机初始化，零值代入会有问题，权重难更新
我们将初始化权值 \(\Theta_{ij}^{(l)}\) 的范围限定在 \([-\Phi ,\Phi ]\) 。

6、Advice for applying machine learning

评价拟合函数hypothesis

1. 分类数据集（training set、test set）
2. 用训练集的theta 计算测试集的误差（分类问题，误差定义为0/1，最终统计结果表现为错误率）
   ### 模型选择——（Train/ Validation/ Test sets）
3. 训练多个模型，在测试集中找到表现最优
4. 偏差和方差（Bias/ Variance）
   关于 模型种类 关于 正则化参数

学习曲线

High bias

High Variance

6.2 设计神经网络

1. 快速部署、设计简单网络
2. plot 学习曲线，发现问题
3. 误差分析（验证集）：数值被错误分类的特征，度量误差

误差度量 for skewed classes 偏斜类

precision/recall

针对最后一级h(x)，
防止错判，阈值提高，设定逻辑判断阈值0.9 instead of 0.5
防止漏过1，阈值放低

综合评定标准

7、支持向量机SVM（support vector machine）

7.1 SVM 大间距分类器（Large Margin Classification）

重写了cost function 和 h（z）

支持向量机的代价函数为：
\[min_{\theta} C[\sum_{i=1}^{m}{y^{(i)}}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})]+\frac{1}{2}\sum_{j=1}^{n}{\theta_j^2}\]

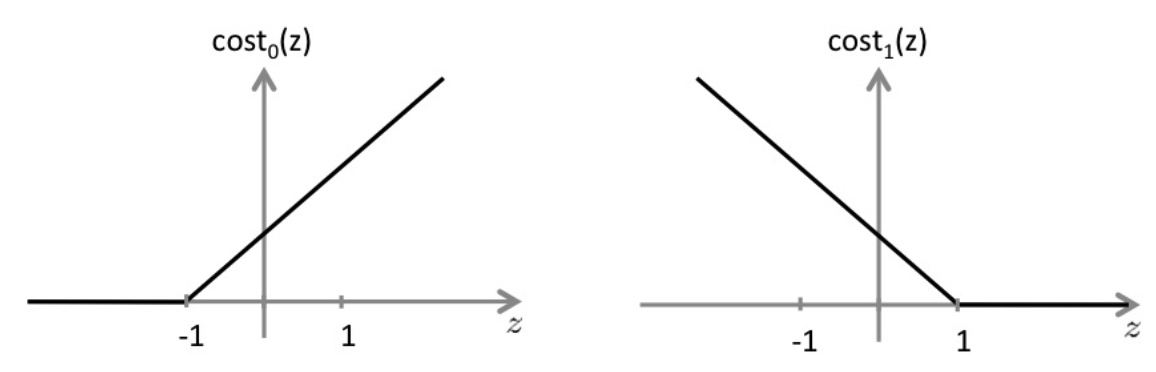
有别于逻辑回归假设函数输出的是概率，支持向量机它是直接预测 y 的值是0还是
假设函数
\[h_{\theta}(x)=\left\{\begin{matrix}
1,\;\;if\; \theta^{T}x\geqslant 0\\
0,\;\;otherwise
\end{matrix}\right.\]

最小化\(\theta\)的模，相当于最大化样本在\(\theta\)上的投影长度，图中直观表现为，绿色边界在\(\theta\)方向上距离样本距离最远。

7.2 kernels核函数

核函数满足\(κ(xi·xj)=φ(xi)T·φ(xj)\)
低维线性不可分（欠拟合）->映射到高维
避免维度灾难，引入核函数（Kernels），用样本去构造特征
适用于n<<m, 增加特征数量变为m

高斯核函数

参数：\(l(i),\sigma\)
\(f = exp^{(-\frac{||x-l^{(i)}||^2}{2\sigma^2})}\)
取值[0,1]

注意的点

核函数用于逻辑回归，运算很慢
核函数优化算法仅适用于SVM
使用前，一定归一化处理

分类模型的选择

7.3 分类模型的选择
目前，我们学到的分类模型有：
（1）逻辑回归；
（2）神经网络；
（3）SVM
怎么选择在这三者中做出选择呢？我们考虑特征维度 n 及样本规模 m ：

1. 如果 n 相对于 m 非常大，例如 n=10000 ，而 \(m\in(10,1000)\) ：此时选用逻辑回归或者无核的 SVM。
2. 如果 n 较小，m 适中，如 \(n\in(1,1000)\) ，而 \(m\in(10,10000)\) ：此时选用核函数为高斯核函数的 SVM。
3. 如果 n 较小，m 较大，如 \(n\in(1,1000)\) ，而 m>50000 ：此时，需要创建更多的特征（比如通过多项式扩展），再使用逻辑回归或者无核的 SVM。 神经网络对于上述情形都有不错的适应性，但是计算性能上较慢。

8、无监督学习（Unsupervised learning）

8.1 分类K-means algorithm(Clustering)

1. cluster 分类，计算到\(\mu_k\)距离将下表k分配给\(c_i\)的
2. 移动cluster central到，分类的平均点
   #### 优化目标
   Cost function
   找到\(c_i\) 和 \(\mu_k\)，使函数：
   \[J(c^{(1)},c^{(2)},\cdots ,c^{(m)};\mu_1,\mu_2,\cdots ,\mu_k)=\frac{1}{m}\sum_{i=1}^m\left \| x^{(i)}-\mu_c(i) \right \|^2\]

\(c_i\in[1,K]\)

\(\mu_k\)随机初始化，避免局部最优

1. k<m
2. 随机指定\(\mu_k = x(i)\)
3. 多次运算，找最优结果
   小k时，多次初始化进行运算
   #### 选择cluster 数量
   plot cluster 数量 为横坐标，找突变点

8.2 Dimensionality reduction

数据压缩 Data Compression

减少冗余特征变量

可视化

PCA主成分分析法（Principal Component Analysis）

PCA算法流程

1. 特征压缩
   假定我们需要将特征维度从 n 维降到 k 维。则 PCA 的执行流程如下：
   特征标准化，平衡各个特征尺度：
   \[x^{(i)}_j=\frac{x^{(i)}_j-\mu_j}{s_j}\]
   \(\mu_j\) 为特征 j 的均值，sj 为特征 j 的标准差。
   计算协方差矩阵 \(\Sigma \) ：
   \[\Sigma =\frac{1}{m}\sum_{i=1}{m}(x^{(i)})(x^{(i)})^T=\frac{1}{m} \cdot X^TX\]
   通过奇异值分解（SVD），求取 \(\Sigma \) 的特征向量（eigenvectors）：
   \[(U,S,V^T)=SVD(\Sigma )\]
   从 U 中取出前 k 个左奇异向量，构成一个约减矩阵 Ureduce :
   \[U_{reduce}=(\mu^{(1)},\mu^{(2)},\cdots,\mu^{(k)})\]
   计算新的特征向量： \(z^{(i)}\)
   \[z^{(i)}=U^{T}_{reduce} \cdot x^{(i)}\]

2. 特征还原
   因为 PCA 仅保留了特征的主成分，所以 PCA 是一种有损的压缩方式，假定我们获得新特征向量为：
   \[z=U^T_{reduce}x\]
   那么，还原后的特征 \(x_{approx}\) 为：
   \[x_{approx}=U_{reduce}z\]

3. 信息保留评价
   降维多少才合适？
   从 PCA 的执行流程中，我们知道，需要为 PCA 指定目的维度 k 。如果降维不多，则性能提升不大；如果目标维度太小，则又丢失了许多信息。通常，使用如下的流程的来评估 k 值选取优异：
   求各样本的投影均方误差:
   \[\min \frac{1}{m}\sum_{j=1}^{m}\left \| x^{(i)}-x^{(i)}_{approx} \right \|^2\]
   求数据的总方差variance：
   \[\frac{1}{m}\sum_{j=1}^{m}\left \| x^{(i)} \right \|^2\]
   评估下式是否成立:
   \[\frac{\min \frac{1}{m}\sum_{j=1}^{m}\left \| x^{(i)}-x^{(i)}_{approx} \right \|^2}{\frac{1}{m}\sum_{j=1}^{m}\left \| x^{(i)} \right \|^2} \leqslant \epsilon \]
   其中， \(\epsilon \) 的取值可以为 0.01,0.05,0.10,⋯，假设 \(\epsilon = 0.01 \) ，我们就说“特征间 99% 的差异性得到保留”。
   看\(\Sigma\)矩阵的二范数占比就知道
   

PCA-point

协方差矩阵\(\Sigma\)看主成分
取前k个u构成向量
\(U_{reduce}\in \mathbb{R}^{n\times k}\)
PCA 不能解决过拟合，要用正则化的方式

9、异常检测

9.1高斯分布(Gaussian normal distribution)

\(x\sim N(\mu,\sigma^2)\)
其分布概率为：
\[p(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})\]
其中 \(\mu\) 为期望值（均值）， \(\sigma^2\) 为方差。
在概率论中，对有限个样本进行参数估计
\[\mu_j = \frac{1}{m} \sum_{i=1}^{m}x_j^{(i)}\;\;\;,\;\;\; \delta^2_j = \frac{1}{m} \sum_{i=1}^{m}(x_j^{(i)}-\mu_j)^2\]
这里对参数 \(\mu\) 和参数 \(\delta^2\) 的估计就是二者的极大似然估计。
假定每一个特征 \(x_{1}\) 到 \(x_{n}\) 均服从正态分布，则其模型的概率为：
\[
\begin{align*}
p(x)&amp;=p(x_1;\mu_1,\sigma_1^2)p(x_2;\mu_2,\sigma_2^2) \cdots p(x_n;\mu_n,\sigma_n^2)\\
&amp;=\prod_{j=1}^{n}p(x_j;\mu_j,\sigma_j^2)\\
&amp;=\prod_{j=1}^{n} \frac{1}{\sqrt{2\pi}\sigma_{j}}exp(-\frac{(x_{j}-\mu_{j})^2}{2\sigma_{j}^2})
\end{align*}
\]
当 \(p(x)&lt;\varepsilon\)时，\(x\) 为异常样本。

算法评价

由于异常样本是非常少的，所以整个数据集是非常偏斜的，我们不能单纯的用预测准确率来评估算法优劣，所以用我们之前的查准率（Precision）和召回率（Recall）计算出 F 值进行衡量异常检测算法了。
真阳性、假阳性、真阴性、假阴性
查准率（Precision）与 召回率（Recall）
F1 Score
我们还有一个参数 \(\varepsilon\) ，这个 \(\varepsilon\) 是我们用来决定什么时候把一个样本当做是异常样本的阈值。我们应该试用多个不同的 \(\varepsilon\) 值，选取一个使得 F 值最大的那个 \(\varepsilon\) 。

异常检测与逻辑回归的区别

异常检测数据特点是：

1. 数据偏斜，y=1数据量极少
2. 异常数据特征不聚类（不稳定），难以预测

多元高斯函数

其概率模型为： \[p(x;\mu,\Sigma)=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))\]
（其中 \(|\Sigma|\) 是 \(\Sigma\) 的行列式，\(\mu\) 表示样本均值，\(\Sigma\) 表示样本协方差矩阵。）。

其中\(\Sigma\)参数估计：
\[\mu=\frac{1}{m}\sum_{i=1}^{m}{x^{(i)}}\]\[\Sigma=\frac{1}{m}\sum_{i=1}^{m}{(x^{(i)}-\mu)(x^{(i)}-\mu)^T}\]

算法流程-多元高斯分布异常检测

采用了多元高斯分布的异常检测算法流程如下：
选择一些足够反映异常样本的特征 \(x_j\) 。
对各个样本进行参数估计： \[\mu=\frac{1}{m}\sum_{i=1}^{m}{x^{(i)}}\]\[\Sigma=\frac{1}{m}\sum_{i=1}^{m}{(x^{(i)}-\mu)(x^{(i)}-\mu)^T}\]
当新的样本 x 到来时，计算 \(p(x)\) ：
\[p(x)=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))\]
如果 \(p(x)&lt;\varepsilon \) ，则认为样本 x 是异常样本。

相关性

一般高斯模型：
需要手动创建一些特征来描述某些特征的相关性
多元高斯模型：
利用协方差矩阵\(\Sigma\)获得了各个特征相关性

复杂度

一般高斯模型：
计算复杂度低，适用于高维特征
多元高斯模型：
计算复杂

效果¶

一般高斯模型：
在样本数目 m 较小时也工作良好
多元高斯模型：
需要 \(\Sigma\) 可逆，亦即需要 \(m&gt;n\) ，(通常会考虑 \( m \geqslant 10*n \)，确保有足够多的数据去拟合这些变量，更好的去评估协方差矩阵 \(\Sigma\) )且各个特征不能线性相关，如不能存在 \(x_2=3x_1\) 或者 \(x_3=x_1+2x_2\)

结论：

基于多元高斯分布模型的异常检测应用十分有限。

9、2 推荐器 Recommender system

Content based recommendations

\(y(i,j) = \theta_{j}^T x_i\)评分等于电影特征成分*用户喜好
前提：电影特征\(x_i\)已知，求解用户喜好\(\theta_j\)

为了对用户 j 打分状况作出最精确的预测，我们需要：
\[\min_{(\theta^{(j)})}=\frac{1}{2}\sum_{i:r(i,j)=1}^{}{((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2}+\frac{\lambda}{2}\sum_{k=1}^{n}{(\theta_k^{(j)})^2}\]
计算出所有的 \(\theta\) 为：
\[J(\theta^{(1)},\cdots,\theta^{(n_u)})=\min_{(\theta^{(1)},\cdots,\theta^{(n_u)})}=\frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}^{}{((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2}+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}{(\theta_k^{(j)})^2}\]
与前面所学线性回归内容的思路一致，为了计算出 \(J(\theta^{(1)},\cdots,\theta^{(n_u)})\)，使用梯度下降法来更新参数：
更新偏置（插值）：
\[\theta^{(j)}_0=\theta^{(j)}_0-\alpha \sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x^{(i)}_0\]
更新权重：
\[\theta^{(j)}_k=\theta^{(j)}_k-\alpha \left( \sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x^{(i)}_k+\lambda \theta^{(j)}_k \right),\;\;\; k \neq 0\]

协同过滤Collaborative filtering

电影特征成分\(x_i\)和用户喜好\(\theta_j\)均未知

算法实现

1. 目标优化
   当用户给出他们喜欢的类型，即 \(\theta^{(1)},\cdots,\theta^{(n_u)}\) ，我们可以由下列式子得出 \(x^{(i)}\) ：
   \[\min_{(x^{(i)})}=\frac{1}{2}\sum_{j:r(i,j)=1}^{}{((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2}+\frac{\lambda}{2}\sum_{k=1}^{n}{(x_k^{(i)})^2}\]
   可出所有的 x 则为：
   \[\min_{(x^{(1)},\cdots,x^{(n_m)})}=\frac{1}{2}\sum_{i=1}^{n_m}\sum_{j:r(i,j)=1}^{}{((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2}+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}{(x_k^{(i)})^2}\]
   只要我们得到 \(\theta\) 或者 x ，都能互相推导出来。
   协同过滤算法基本思想就是当我们得到其中一个数据的时候，我们推导出另一个，然后根据推导出来的再推导回去进行优化，优化后再继续推导继续优化，如此循环协同推导。
2. 协同过滤的目标优化
   推测用户喜好：给定\(x^{(1)},\cdots,x^{(n_m)}\) ，估计\(\theta^{(1)},\cdots,\theta^{(n_\mu)}\) ： \[\min_{(\theta^{(1)},\cdots,\theta^{(n_\mu)})}=\frac{1}{2}\sum_{j=1}^{n_\mu}\sum_{i:r(i,j)=1}^{}{((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2}+\frac{\lambda}{2}\sum_{j=1}^{n_\mu}\sum_{k=1}^{n}{(\theta_k^{(j)})^2}\]
   推测商品内容：给定\(\theta^{(1)},\cdots,\theta^{(n_\mu)}\) ，估计\(x^{(1)},\cdots,x^{(n_m)}\) ： \[\min_{(x^{(1)},\cdots,x^{(n_m)})}=\frac{1}{2}\sum_{i=1}^{n_m}\sum_{j:r(i,j)=1}^{}{((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2}+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}{(x_k^{(i)})^2}\]
   协同过滤：同时优化\(x^{(1)},\cdots,x^{(n_m)}\) ，估计\(\theta^{(1)},\cdots,\theta^{(n_\mu)}\)： \[\min \; J(x^{(1)},\cdots,x^{(n_m)};\theta^{(1)},\cdots,\theta^{(n_\mu)})\]
   即：
   \[\min_{(x^{(1)},\cdots,x^{(n_m)};\theta^{(1)},\cdots,\theta^{(n_\mu)})}=\frac{1}{2}\sum_{(i,j):r(i,j)=1}^{}{((\theta^{(j)})^T(x^{(i)})-y^{(i,j)})^2}+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}{(x_k^{(i)})^2}+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}{(\theta_k^{(j)})^2}\]
   因为正则化的原因在这里面不再有之前的 \(x_0=1\),\(\theta_0=0\) 。
3. 协同过滤算法的步骤为：
   随机初始化\(x^{(1)},\cdots,x^{(n_m)},\theta^{(1)},\cdots,\theta^{(n_\mu)} \)为一些较小值，与神经网络的参数初始化类似，为避免系统陷入僵死状态，不使用 0 值初始化。
   通过梯度下降的算法计算出\(J(x^{(1)},\cdots,x^{(n_m)},\theta^{(1)},\cdots,\theta^{(n_\mu)})\),参数更新式为： \[x^{(i)}_k=x^{(i)}_k-\alpha \left( \sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})\theta^{(j)}_k+\lambda x^{(i)}_k \right)\]\[\theta^{(j)}_k=\theta^{(j)}_k-\alpha \left( \sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x^{(i)}_k+\lambda \theta^{(j)}_k \right)\]
   如果用户的偏好向量为\(\theta\)，而商品的特征向量为 x ，则可以预测用户评价为 \(\theta^Tx\) 。
   因为协同过滤算法 \(\theta\) 和 x 相互影响，因此，二者都没必要使用偏置 \(\theta_0\) 和 \(x_0\)，即，\(x \in \mathbb{R}^n\)、 \(\theta \in \mathbb{R}^n\) 。
   #### 低秩分解（Low Rank Matrix Factorization）
   \(Y = X\Theta^T\)

正则化

1. \(\lambda\)正则化，使\(\theta\)趋向0
2. 平均值正则化(mean normalization)
   将平均值作为0点，让Y偏置

10、大数据集——提升运算速度

Stochastic Gradient Descent（随机梯度下降法）

不用全部数据集进行运算

1. 预处理，随机排序
2. 内循环，单个特征修改拟合参数
   每次使用一个样本
   #### SGD收敛性
   每隔1000个样本画cost函数
3. 小\(\alpha\)让曲线慢，准
4. 大样本采样间距->曲线更光滑
5. 随着迭代次数，减小α

Mini-Batch Gradient Descent

矢量化->并行计算，提高效率

在线学习Online learning

数据集连续，减少存储成本

Map reduce and data parallelism

代数计算库自动implement

12、Photo OCR pipeline

1. 文本检测
2. 特征分割
3. 特征识别
4. 修正C1eaning->cleaning
   ### Sliding window 滑窗分类器
   #### 文本检测
   步长step size
   不同大小，按照比例缩放

检测到特征，相邻互联

特征分割

获取数据，人造数据

1. 加背景噪音
2. 字体处理
3. 人工扭曲

加入高斯噪声没用

大量数据获取建议

Ceiling analysis上限分析

找到提升最大的Module

强化学习

连接

一些概念

• 向量机

• 核函数
  作用：
  减小计算量，解决多维输入问题
  无需知道非线性变换函数的形式和参数

核函数种类

• 贝叶斯滤波器：概率滤波器

处理微分的手段

1. 微分+一阶惯性环节，\(tf = s/(T_s s +1)\)
2. TD微分跟踪器
3. 状态观测器
4. 卡尔曼滤波器