循序渐进学习栈和队列

一、栈

1.栈的定义：

是限定仅在表尾进行插入或删除操作的线性表。因此，对栈来说，表尾端有其特殊含义称为栈顶，相应地，表头端称为栈底。栈的修改是按后进先出的原则进行的，因此又称后进先出表。

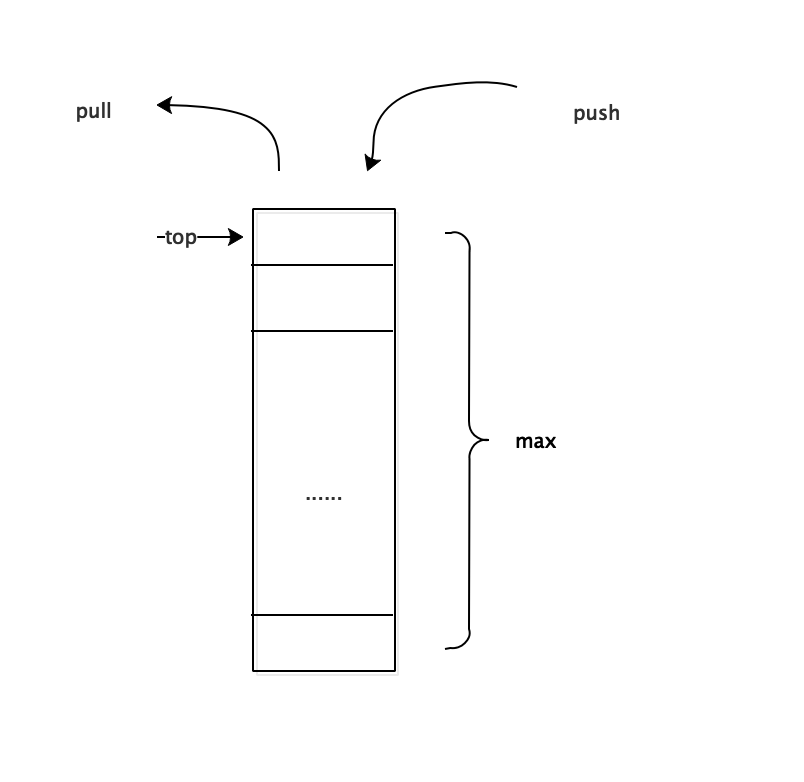
解释：栈是一个很简单的数据结构，但是好多人不能理解它的重要的特性，即只能在栈顶的位置进行操作，可以理解栈是一个水杯，只能在杯口倒水或者喝水。

2.栈的定义和特点：

1.定义：只能在表的一端（栈顶）进行插入和删除运算的线性表

2.逻辑结构：与线性表相同，仍为一对一关系

3.存储结构：用顺序栈或链栈存储均可，但以顺序栈更常见（本文探讨顺序栈）

4.运算规则：只能在栈顶运算，且访问结点时依照后进先出（LIFO）或先进后出（FILO）的原则

5.实现方式：关键是编写入栈和出栈函数，具体实现依顺序栈或链栈的不同而不同。

3.顺序栈的基本操作

1.初始化

typedef struct{
   int data[maxsize];
   int top;
}Sqstack;  // 顺序栈类型定义


void init(Sqstack &st){
  st.top = -1;
}

2.判断栈空

int isEmpty(Sqstack st){
 if (st.top == -1)
    return 1;
 else 
    return 0;
}

3.进栈

int push(Sqstack &st ,int x){
// 栈满，不能进栈
  if (st.top == maxSize - 1)
  return 0;
  // 先移动指针，再进栈
  ++ (st.top);
  st.data[st.top] = x;
  return 1;

}

4.出栈

int pop (Sqstack &st, int &x){
 // 空栈，不能出栈
  if (st.top == -1)
     return 0;
  // 先取出元素，再移动指针
  x = data[st.top];
  -- st.top;
    return 1;

}

三、队列

1.队列的定义：

是一种先进先出的线性表，它只允许在表的一端进行插入，而在另一端删除元素，在队列中，允许插入的一端称做队尾，允许删除的一端称做队头。

解释：队列是一个很简单的数据结构，从队尾插入，队头删除，可以理解队列是一个单行道，如图可知。

2.队列的定义和特点：

1.定义：只能在表的一端（队尾）进行插入，在另一端（队头）进行删除运算的线性表

2.逻辑结构：与线性表相同，仍为一对一关系

3.存储结构：用顺序队列或链队存储均可

4.运算规则：先进先出（FIFO）

5.实现方式：关键是编写入队和出队函数，具体实现依顺序队或链队的不同而不同

3.队列的基本操作

#define M  100   //最大队列长度
Typedef struct {
   QElemType *base;  //初始化的动态分配存储空间
   int  front;            //头指针   
   int  rear;             //尾指针
}SqQueue;

空队标志：front= =rear
入队：base[rear++]=x;
出队：x=base[front++];

4.循环队列

介绍循环队列之前首先来看看一种现象：

这种现象也是队列的弊端，发生假溢出现象。如果解决-----循环队列

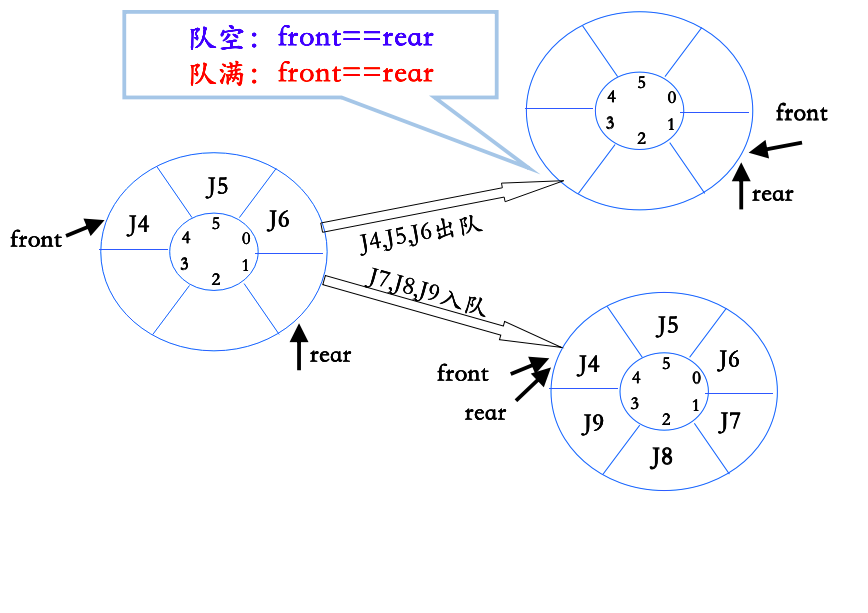
如上图可以知道，循环队列的入队和出队的条件一样。没办法区分。

解决方案：
1.另外设一个标志以区别队空、队满

2.少用一个元素空间：队空：frontrear；队满：(rear+1)%Mfront

5.循环队列的基本操作

#define MAXQSIZE  100  //最大长度
Typedef struct {
   QElemType *base;  //初始化的动态分配存储空间
   int  front;            //头指针   
   int  rear;             //尾指针
}SqQueue; 

1.循环队列初始化：

Status InitQueue (SqQueue &Q){
    Q.base =new QElemType[MAXQSIZE] 
   if(!Q.base) exit(OVERFLOW);
    Q.front=Q.rear=0;
    return OK;
}

2.求循环队列长度：

int  QueueLength (SqQueue Q){
    return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;                             
 }

3.循环队列入队：

Status EnQueue(SqQueue &Q,QElemType e){
    if((Q.rear+1)%MAXQSIZE==Q.front)  return ERROR;
    Q.base[Q.rear]=e;
    Q.rear=(Q.rear+1)%MAXQSIZE;
     return OK;
}

4.循环队列出队：

Status DeQueue (LinkQueue &Q,QElemType &e){
   if(Q.front==Q.rear) return ERROR;
   e=Q.base[Q.front];
   Q.front=(Q.front+1)%MAXQSIZE;
   return OK;
}

---

欢迎关注公众号coder辰砂，一个认认真真写文章的公众号。