循序渐进学习数据结构之线性表
一、思维导图
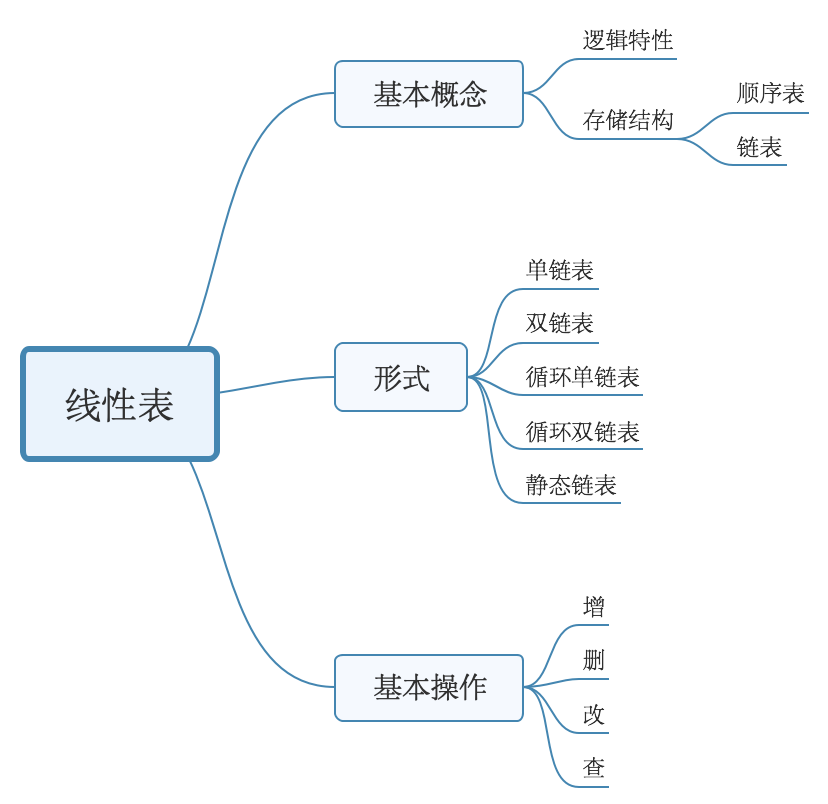
二、线性表的基本概念
1.名词解释:
线性表:由n个数据特性相同的元素构成的有限序列,有顺序存储和链式存储两种表示形式。

空表:线性表中元素的个数n=0的表。
线性表的链式存储结构:特点是用一组任意的存储单元存储线性表的数据元素,包括两个域,其中存储数据元素信息的域称为数据域,存储直接后继存储位置的域称为指针域。
循环单链表:是另一种形式的链式存储结构。它的特点是表中最后一个结点的指针域指向头结点,整个链表形成一个环。
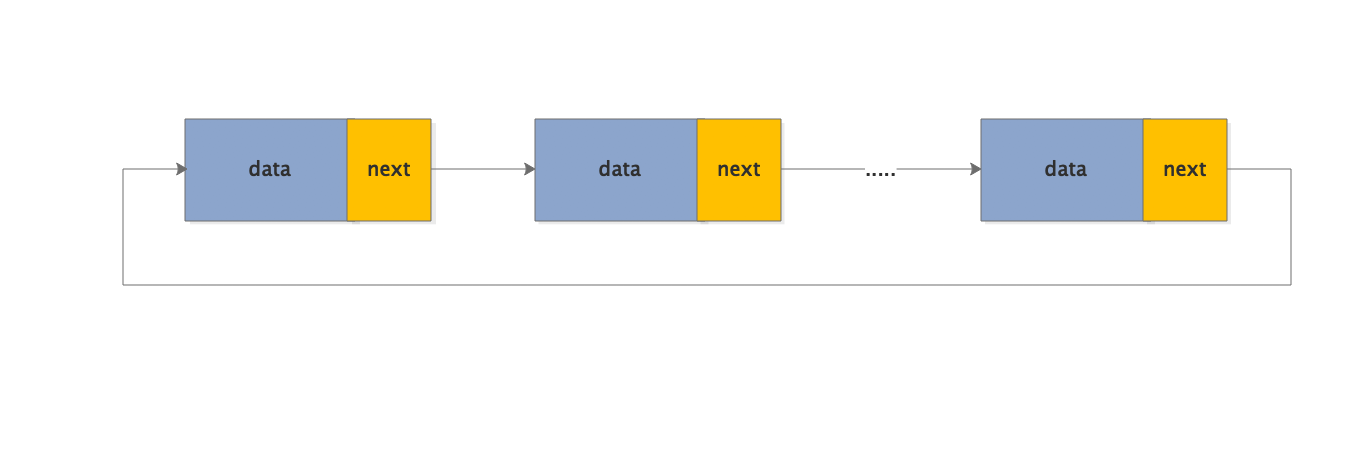
循环双链表:是另一种形式的链式存储结构。它的特点是表中最后一个结点的指针域指向头结点,头节点同时指向最后一个节点,整个链表形成一个环。(这个图画的太丑啦!!)

双向链表:是指有两个指针域,其一指向直接后继,另一指向直接前趋。
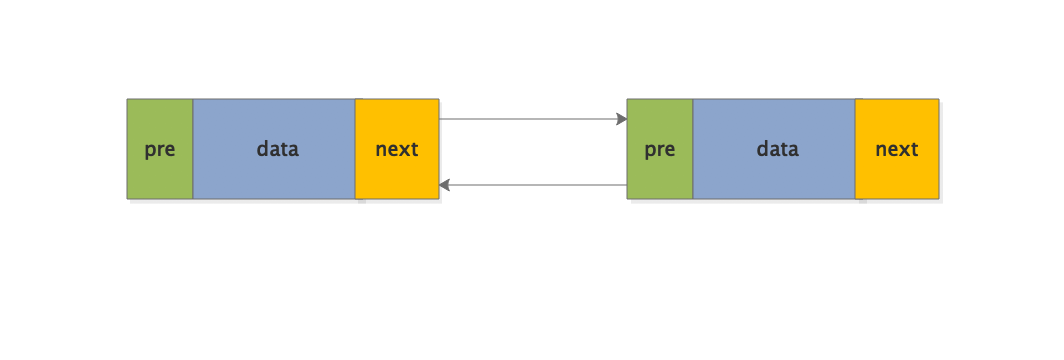
线性结构:若结构是非空有限集,则有且仅有一个开始结点和一个终端结点,并且所有结点都最多只有一个直接前趋和一个直接后继。
非空线性表或线性结构特点: 1.存在唯一的一个被称作“第一个”的数据元素;2.存在唯一的一个被称作“最后一个”的数据元素;3.除第一个之外,结构中的每个数据元素均只有一个前驱;4.除最后一个之外,结构中的每个数据元素均只有一个后继
2.存储结构
1.顺序表
1.特点
(一)利用数据元素的存储位置表示线性表中相邻数据元素之间的前后关系,即线性表的逻辑结构与存储结构一致
(二)在访问线性表时,可以快速地计算出任何一个数据元素的存储地址。因此可以粗略地认为,访问每个元素所花时间相等
这种存取元素的方法被称为随机存取法
2.优缺点
优点: 存储密度大(结点本身所占存储量/结点结构所占存储量);可以随机存取表中任一元素
缺点:在插入、删除某一元素时,需要移动大量元素;浪费存储空间;属于静态存储形式,数据元素的个数不能自由扩充。
为了克服这样的缺点---链表
2.链表
链表各结点由两个域组成:数据域:存储元素数值数据;指针域:存储直接后继结点的存储位置
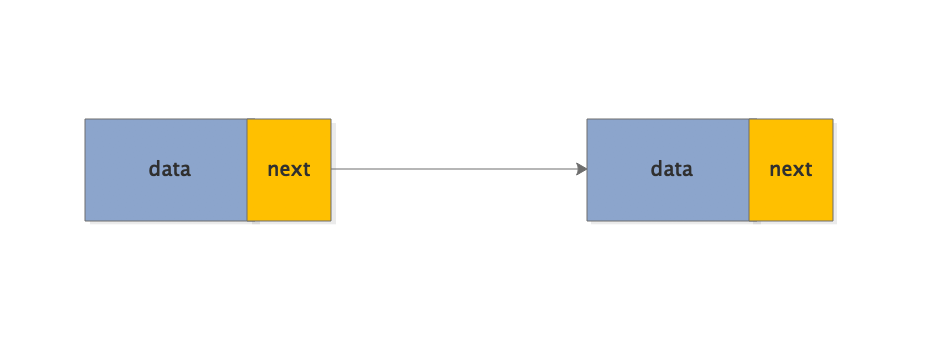
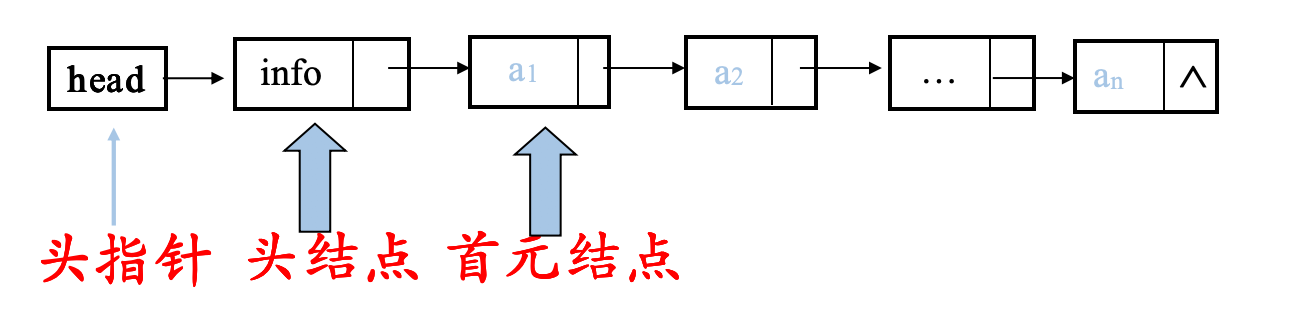
头指针:指向链表中第一个结点的指针
头结点:在链表的首元结点之前附设的一个结点;数据域内只放空表标志和表长等信息
首元结点:指链表中存储第一个数据元素a1的结点
链表中设置头结点的好处:
⒈便于首元结点的处理
首元结点的地址保存在头结点的指针域中,所以在链表的第一个位置上的操作和其它位置一致,无须进行特殊处理;⒉便于空表和非空表的统一处理
无论链表是否为空,头指针都是指向头结点的非空指针,因此空表和非空表的处理也就统一了。
头结点的数据域可以为空,也可存放线性表长度等附加信息,但此结点不能计入链表长度值。
1.特点
(一)结点在存储器中的位置是任意的,即逻辑上相邻的数据元素在物理上不一定相邻
(二)访问时只能通过头指针进入链表,并通过每个结点的指针域向后扫描其余结点,所以寻找第一个结点和最后一个结点所花费的时间不等
这种存取元素的方法被称为顺序存取法
2.优缺点
优点: 存储密度小(结点本身所占存储量/结点结构所占存储量);删除或者插入操作时间复杂度低
缺点:在查询的时候需要从头节点开始查找,时间复杂度高。
为了克服这样的缺点---双链表,循环链表等
三、线性表的基本操作
1.顺序表的基本操作:
1.初始化顺序表(参数用引用):
Status InitList_Sq(SqList &L){ //构造一个空的顺序表L
L.elem=new ElemType[MAXSIZE]; //为顺序表分配空间
if(!L.elem) exit(OVERFLOW); //存储分配失败
L.length=0; //空表长度为0
return OK;
}
1.初始化顺序表(参数用指针):
Status InitList_Sq(SqList *L){ //构造一个空的顺序表L
L->elem=new ElemType[MAXSIZE]; //为顺序表分配空间
if(!L->elem) exit(OVERFLOW); //存储分配失败
L->length=0; //空表长度为0
return OK;
}
2.取值(根据位置i获取相应位置数据元素的内容) :
int GetElem(SqList L,int i,ElemType &e)
{
if (i<1||i>L.length)
return 0; //判断i值是否合理,若不合理,返回0
e=L.elem[i-1]; //第i-1的单元存储着第i个数据
return 1;
}
3.查找(根据指定数据获取数据所在的位置 ) :
在线性表L中查找值为e的数据元素
int LocateELem(SqList L,ElemType e)
{
for (i=0;i< L.length;i++)
if (L.elem[i]==e) return i+1;
return 0;
}
4.插入(插入到第i个结点之前 ) :
Status ListInsert_Sq(SqList &L,int i ,ElemType e){
if(i<1 || i>L.length+1) return ERROR; //i值不合法
if(L.length==MAXSIZE) return ERROR; //当前存储空间已满
for(j=L.length-1;j>=i-1;j--)
L.elem[j+1]=L.elem[j]; //插入位置及之后的元素后移
L.elem[i-1]=e; //将新元素e放入第i个位置
++L.length; //表长增1
return OK;
}
5.删除(删除第i个结点) :
Status ListDelete_Sq(SqList &L,int i){
if((i<1)||(i>L.length)) return ERROR; //i值不合法
for (j=i;j<=L.length-1;j++)
L.elem[j-1]=L.elem[j]; //被删除元素之后的元素前移
--L.length; //表长减1
return OK;
}
2.单链表的基本操作:
1. 初始化
【算法步骤】
(1)生成新结点作头结点,用头指针L指向头结点。
(2)头结点的指针域置空。
Status InitList_L(LinkList &L){
L=new LNode;
L->next=NULL;
return OK;
}
2. 取值(根据位置i获取相应位置数据元素的内容)
Status GetElem_L(LinkList L,int i,ElemType &e){
p=L->next;j=1; //初始化
while(p&&j<i){ //向后扫描,直到p指向第i个元素或p为空
p=p->next; ++j;
}
if(!p || j>i)return ERROR; //第i个元素不存在
e=p->data; //取第i个元素
return OK;
}
3. 查找
根据指定数据获取数据所在的位置
// 在链表L中查找值为e的数据元素,并返回该结点
LNode *LocateELem_L (LinkList L,Elemtype e) {
//返回L中值为e的数据元素的地址,查找失败返回NULL
p=L->next;
while(p &&p->data!=e)
p=p->next;
return p;
}
4.插入
【算法步骤】
(一)找到ai-1存储位置p
(二)生成一个新结点*s
(三)将新结点*s的数据域置为x
(四)新结点*s的指针域指向结点ai
(五)令结点p的指针域指向新结点s
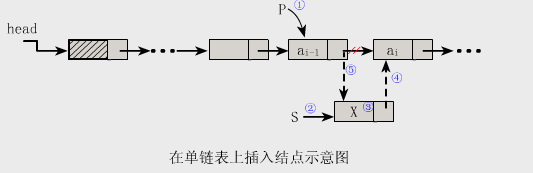
// 核心代码
s->next=p->next;
p->next= s;
//在L中第i个元素之前插入数据元素e
Status ListInsert_L(LinkList &L,int i,ElemType e){
p=L;j=0;
while(p&&j<i−1){p=p->next;++j;} //寻找第i−1个结点
if(!p||j>i−1)return ERROR; //i大于表长 + 1或者小于1
s=new LNode; //生成新结点s
s->data=e; //将结点s的数据域置为e
s->next=p->next; //将结点s插入L中
p->next=s;
return OK;
}//ListInsert_L
5.删除
【算法步骤】
(一)找到ai-1存储位置p
(二)保存要删除的结点的值
(三)令p->next指向ai的直接后继结点
(四)释放结点ai的空间
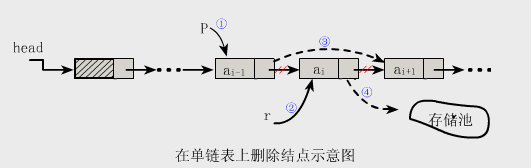
int ListDelete_L(LinkList &L,int i,ElemType &e){
p=L;j=0;
while(p->next &&j<i-1){ //寻找第i个结点,并令p指向其前驱
p=p->next; ++j;
}
if(!(p->next)||j>i-1) return 0; //删除位置不合理
q=p->next; //临时保存被删结点的地址以备释放
p->next=q->next; //改变删除结点前驱结点的指针域
e=q->data; //保存删除结点的数据域
delete q; //释放删除结点的空间
return 1;
}
3.双向链表的基本操作
1.双向链表的插入:

// 核心代码
1. s->prior=p->prior;
2. p->prior->next=s;
3. s->next=p;
4. p->prior=s;
Status ListInsert_DuL(DuLinkList &L,int i,ElemType e){
if(!(p=GetElemP_DuL(L,i))) return ERROR;
s=new DuLNode;
s->data=e;
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;
return OK;
}
2.双向链表的删除:
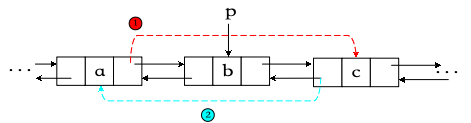
// 核心代码
1. p->prior->next=p->next;
2. p->next->prior=p->prior;
Status ListDelete_DuL(DuLinkList &L,int i,ElemType &e){
if(!(p=GetElemP_DuL(L,i))) return ERROR;
e=p->data;
p->prior->next=p->next;
p->next->prior=p->prior;
delete p;
return OK;
}
4.循环链表的基本操作
理解单链表和双向链表的操作,循环链表的操作也类似。这里不在赘述。
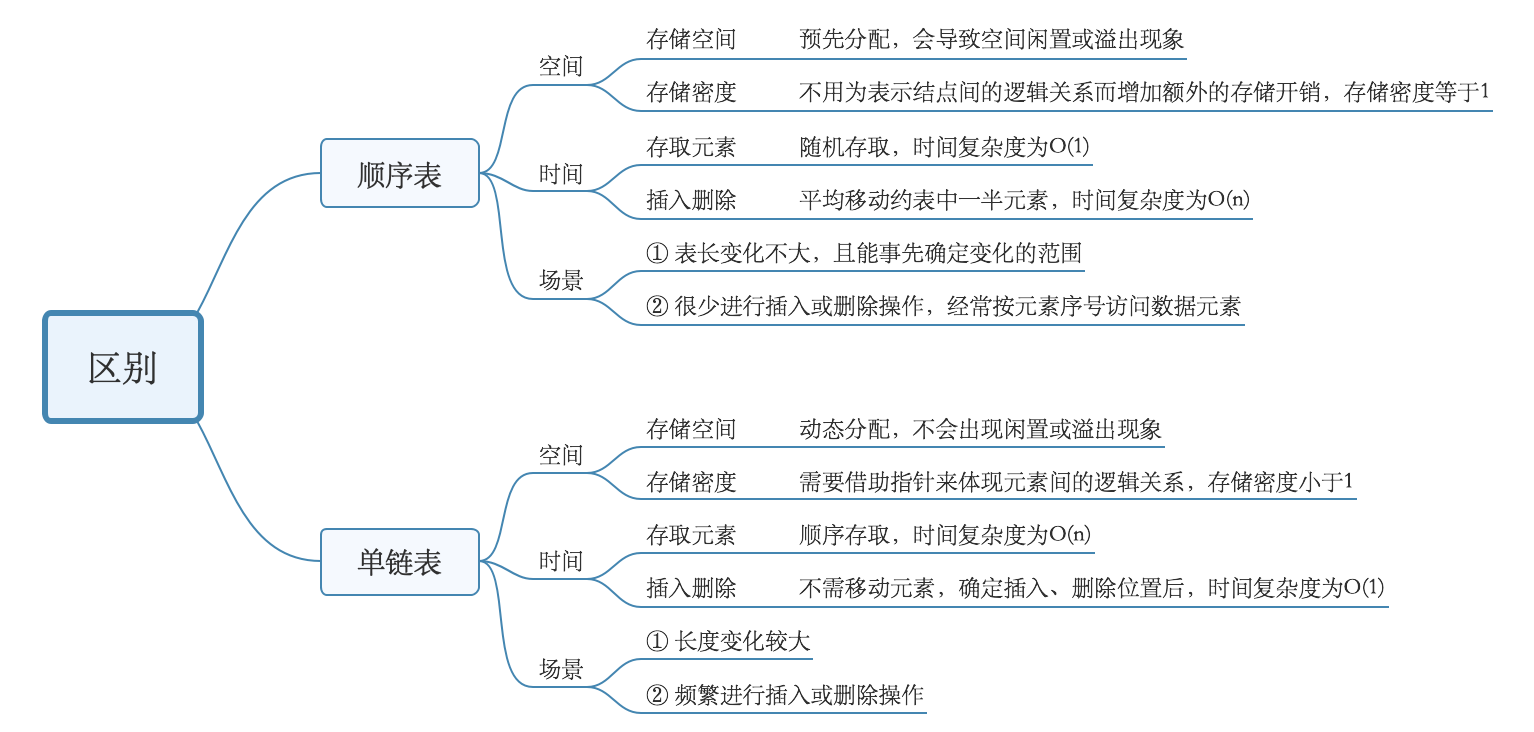
四、比较顺序表和单链表
欢迎关注公众号:coder辰砂 (一个认认真真写东西的公众号)



