[吴恩达深度学习课程笔记13]序列模型-循环序列模型
05. 序列模型
第一周 循环序列模型
1.1 序列数据
有大量的任务处理的都是序列数据,所以我们需要一个序列模型。(按吴恩达老是这么说,我做的视频任务应该也是序列数据)

1.2 符号表示
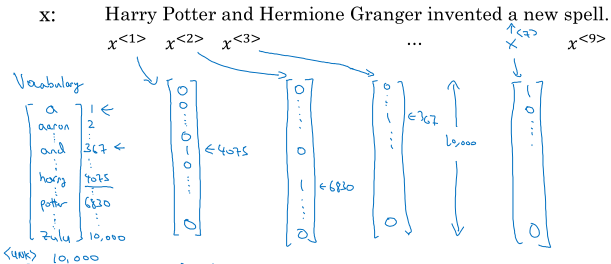
以自然语言处理(NLP)任务为例,一个句子记为一个样本\( x^{(i)} \),句子中的每个词记为\( x^{(i)<t>} \),句子的长度记为\( T_x^{(i)} \)。
怎么表示句子中的单词呢?首先我们要有一个词典,例如10000词,然后用one-hot形式表示一个单词出现在词典中的位置,所以一个单词可以用一个10000维的向量来表示,这个向量中只有一个非零元素1.
1.3 & 1.4 循环神经网络模型
不采用标准神经网络处理文本的原因:输入和输出的长度都不确定(其实可以填充到最大长度);在文本不同位置学习到的特征并不共享(重复的词)。
循环神经网络(recurrent neural network, RNN)的结构如下:

在处理文本时,每个时间步的输出不仅取决于当前时刻的词,还要利用前一时刻激活值。这也是循环神经网络的缺点,只能利用之前时刻的信息,看不到之后的信息。
前向传播的计算过程:
\( a^{<0>} = 0 \)
\( a^{<t>} = g_1(W_{aa}a^{<t-1>} + W_{ax}x^{<t>} + b_a) \)
\( \hat{y}^{<t>} = g_2(W_{ya}a^{<t>} + b_y) \)
RNN中常用tanh作为激活函数,其中\( g_1, g_2 \)可以不一样,\(g_2\)的选择要依赖于输出形式,可能是sigmoid或者softmax.
借助于矩阵运算的话,上述的算式可以简化为:
\( a^{<t>} = g_1(W_{a} \begin{bmatrix}a^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_a) \)
\( \hat{y}^{<t>} = g_2(W_{y}a^{<t>} + b_y) \)
\( W_a = [W_{aa} \vdots W_{ax}] \)
定义单步的损失函数:\( L^{<t>} (\hat{y}^{<t>}, y^{<t>}) = - y^{<t>} \log (\hat{y}^{<t>}) - (1 - y^{<t>}) \log (1 - \hat{y}^{<t>}) \)
整体的代价函数:\( \begin{gathered} L(\hat{y}, y) = \sum_{t = 1}^{T_x}L^{<t>}(\hat{y}^{<t>},y^{<t>}) \end{gathered}\)
完整的前向传播和反向传播流程:
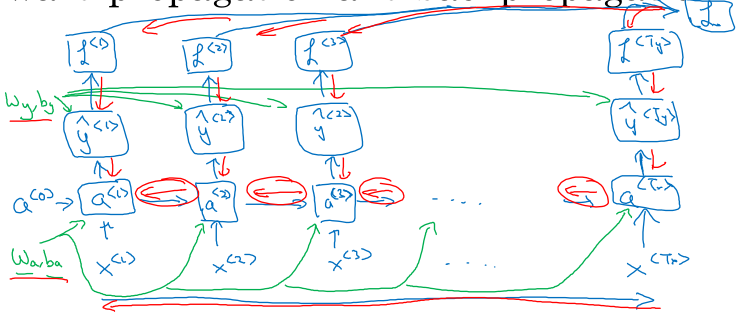
注意每个时间步的 \( a^{<t>} \),都要传给下个时间步,而网络参数其实只有一套,所以是有一个循环结构的,只不过这里按时间展开了。
反向传播则是按照相反的方向进行。
1.5 不同类型的循环神经网络
前面讲的RNN处理的是输入和输出长度相同的任务,对于不同的输入和输出长度有各种网络结构:
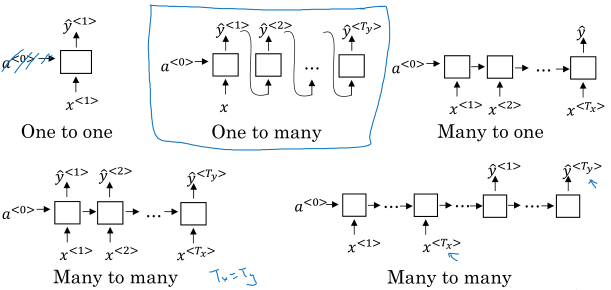
一对多:比如音乐生成;多对一:比如评论打分;多对多:机器翻译(输入和输出长度可能不同)。
1.6 & 1.7 语言模型
语言模型就是对于文本完整性或者正确性的理解,比如能够判断 "The apple and pair salad." 和 "The apple and pear salad." 两个句子的出现的概率哪个更高。
我们可以用RNN对文本进行建模,当输入一段文本时,模型能够给出每个词的概率,从而能够得到整个句子的概率。这其中包含很多工作:
- 要有一个用于训练的语料库(corpus),里面全是文本;
- 利用词典将文本转化为词向量,可能需要标记句子的结尾(EOS),以及词典中不存在的词(UNK);
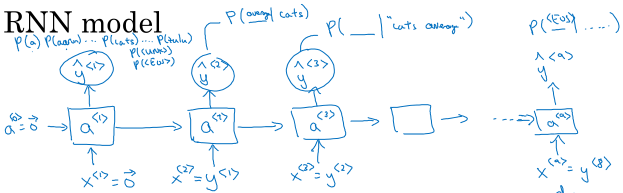
具体的步骤:
第一个时间步,输入\( x^{<1>} = 0, a^{<0>} = 0 \),输出softmax的结果表示文本第一个词可能为某一个词的概率,比如10002个概率(词典加特殊符号)。
第二个时间步,我们会告诉模型第一个词是什么,即\( x^{<2>} = y^{<1>} \),让它预测第二个词某个词的概率,依此类推。
最后整个文本的概率\( P(y^{<1>}, P^{<2>}, P^{<3>}) = P(y^{<1>})P(y^{<2>}|y^{<1>})P(y^{<3>}|y^{<1>}, y^{<2>}) \)
注意,在上面介绍的语言模型中,第一个时间步我们得到了词典中各种词的概率分布,可以自己选择一些词作为第二个时间步的输入,然后再对第二个时间步的输出进行采样作为第三个时间步的输出,以此类推,生成一个文本序列,这就得到了一个采样序列,通过这种方法我们可以用语言模型生成一段文本。
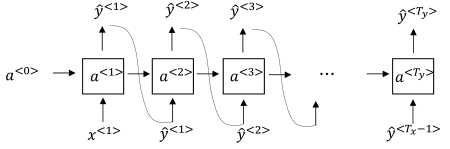
采样序列的结束可以是遇到EOS,也可以是固定长度。同时还要避免句子中出现不确定单词UNK。
这是基于单词的语言模型,还有基于字符的语言模型,在生成的时候需要一个字符一个字符的生成,比如a,p,p,l,e等,这种模型不用担心UNK,但是很难捕捉较长的语义,而且训练更加耗费资源。
1.8 RNN的梯度消失
我们知道神经网络越深越难训练,而且会出现梯度爆炸和梯度消失的问题,其中梯度消失是相对更难的问题。
RNN也有同样的问题,它无法捕捉长期依赖(long-term dependency),例如一个很长的句子:
The cat, which ..., ate ..., was full. 如果要模型能够根据之前的主语选择was/were就要解决这种长期依赖问题。
1.9 GRU
为了解决梯度消失的问题,引入记忆单元\( c^{<t>} \)和其候选值\( \tilde{c}^{<t>} \)。
记忆单元相当于之前的\( a^{<t>} \),不过通过一些门控机制来控制更新。这里的门控(gate)指的是一组介于0~1之间的数,观察下面记忆单元的更新公式,发现候选值和旧的记忆正是通过门控\( \Gamma_u \)来组合形成新的记忆,比如之前的例子中,cat可能会被一直保留在记忆中,能够正确输出was.
完整的GRU公式:
\( \Gamma_u = \sigma \left( W_u \begin{bmatrix}c^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_u \right) \)
\( \Gamma_r = \sigma \left( W_r \begin{bmatrix}c^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_r \right) \)
\( \tilde{c}^{<t>} = tanh(W_c \begin{bmatrix}\Gamma_r * c^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_c) \)
\( c^{<t>} = \Gamma_u * \tilde{c}^{<t>} + (1 - \Gamma_u) * c^{<t-1>} \)
*表示元素乘积,另一个门控\( \Gamma_r \)表示对候选值的控制,这个其实是经验之选。其中\( c^{<t>} \)保持不断更新,而网络的输出\( \tilde{y}^{<t>} \)则是基于\( c^{<t>} \)增加softmax层或者其它层得到的。
1.10 LSTM
LSTM和GRU很相似(其实是先有的LSTM),完整公式如下:
\( \Gamma_u = \sigma \left( W_u \begin{bmatrix}a^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_u \right) \)
\( \Gamma_f = \sigma \left( W_f \begin{bmatrix}a^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_f \right) \)
\( \Gamma_o = \sigma \left( W_o \begin{bmatrix}a^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_o \right) \)
\( \tilde{c}^{<t>} = tanh(W_c \begin{bmatrix}\Gamma_r * c^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_c) \)
\( c^{<t>} = \Gamma_u * \tilde{c}^{<t>} + \Gamma_f * c^{<t-1>} \)
\( a^{<t>} = \Gamma_o * c^{<t>} \)
注意一些不同点:
- 区分 \( a^{<t>}, c^{<t>} \);
- 使用两个门控 \( \Gamma_u, \Gamma_f \) 来控制 \( c^{<t>} \) 的更新。
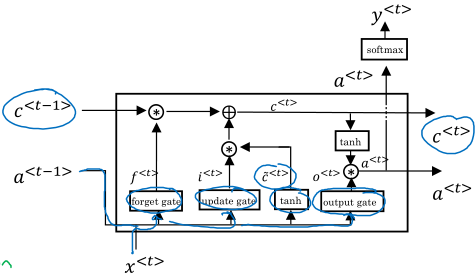
从整个时序上去看:

横贯多个时间步的那条线就是确保模型捕获长期依赖的关键。
LSTM比GRU更有效,门控更多,更复杂;GRU比较简单,可以构建更大的网络。大家的首选还是LSTM。
1.11 双向神经网络
前面讲RNN还有一个问题就是只能利用之前的信息,有些句子如果只看前面的话很难去理解,这时候可以采用双向的结构:
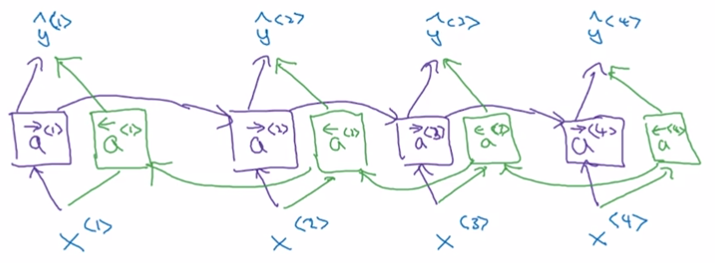
有了前面的标准RNN/GRU/LSTM结构,不仅从前往后计算一遍\( \overrightarrow{a}^{<t>} \),还要从后往前计算一遍\( \overleftarrow{a}^{<t>} \),最后网络的输出变成:
\( \hat{y}^{<t>} = g(W_y \begin{bmatrix}\overrightarrow{a}^{<t>} \\ \overleftarrow{a}^{<t>} \end{bmatrix} + b_y) \)
有个要求:你需要完整的文本才可以。
1.12 深层循环神经网络
前面已经说过了,图中横着那一长串其实不是我们以往理解的那种“深层”,真正的深层网络如下:
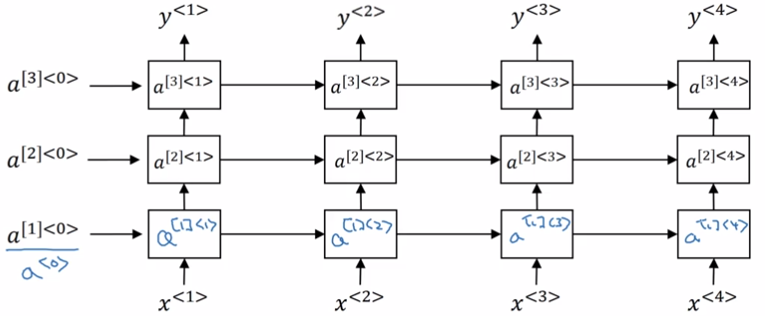
对于RNN来说,这样叠加三层已经够用了,由于时间维度上可能很长,所以网络的规模可能很大。
基本单元不一定是RNN,可以换成GRU,LSTM甚至构建双向网络。
另一种常见的结构是在上面每个时间步的后面加一个比较深的网络,但是这些深层网络没有时间维度上的连接。



