吴恩达深度学习课程笔记-4
02. 改善深度神经网络:超参数调试、正则化和优化
第一周 深度学习的实用层面
1.1 训练/验证/测试集
将全部的数据集分为三部分:训练集、验证集和测试集。其中训练集用于模型的学习,验证集用于确定模型的超参数,测试集用于对模型的性能做出无偏的评估。
传统机器学习的做法是,训练集:测试集=7:3,训练集:验证集:测试集=6:2:2。这一做法同样适用于数据集较小的情况,如100,1000,10000.
大数据时代做法不同,比如数据集规模1000000,只需要10000用作验证集,10000用作测试集即可。当数据规模更大的时候,验证集和测试集的比例可以更小。
在划分数据集时,要尽量确保训练集和测试集服从同一分布。
如果只有验证集没有测试集也是可以的,有的人叫做训练/验证集,有的人叫做训练/测试集。
1.2 & 1.3 偏差/方差
偏差和方差的均衡是非常重要的一个问题,可以用训练集和验证集误差进行衡量
| 验证集误差大 | 验证集误差小 | |
| 训练集误差大 | 偏差大,方差小 | 偏差大,方差大 |
| 训练集误差小 | 偏差小,方差大 | 偏差小,方差小 |
通过训练集和验证集误差,我们可以对偏差和方差进行评估,机器学习中常用的做法是:
- 首先在训练集上检查是否偏差过大,如果偏差过大可以尝试更加复杂的模型;
- 偏差降低之后在验证机上检查方差,如果方差过大可以尝试收集更多训练数据或者利用正则化手段。
通常来说我们需要不断反复尝试,直到找到一个同时降低偏差和方差的方法。
在机器学习时代,方差和偏差权衡的问题引起的讨论很多,因为有很多方法在降低其中一个的同时使另一个升高。而现如今深度学习和大数据时代,我们有办法同时降低方差和偏差,比如只要正则化合适,持续训练一个更加复杂的网络可以不显著影响方差的情况下降低偏差;而采用更多数据可以在不显著影响偏差的情况下降低方差。
1.4 & 1.5 & 1.6 & 1.7 & 1.8 正则化
防止过拟合的方法可以是采用更大的数据集,这比较困难,另一种就是正则化。
正则化可以选择 \( L_1, L_2 \) 正则等,\( L_1 \)正则项会产生更加稀疏的解,但现在 \( L_2\) 正则使用的更多。
加入 \(L_2\) 正则化项的神经网络代价函数为:
\( \begin{gathered} J = \frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m}\sum_{l=1}^{L}\| W^{[l]} \|^2_F \end{gathered} \)
其中\( \begin{gathered} \| W^{[l]} \|^2_F = \sum_{i=1}^{n^{[l]}} \sum_{j=1}^{n^{[l-1]}} (w_{ij}^{[l]})^2 \end{gathered} \) 称为Frobenius范数。
\( L_2 \) 正则又被称为权重衰减(weight decay),原因在于对应的梯度下降公式为:
\( W^{[l]} = W^{[l]} - \alpha [(\text{from backprop }) + \frac{\lambda}{m}W^{[l]}] \)
很容易想到,加入正则化项可以使得模型的参数值偏小,这相当于削弱了神经网络中各个神经元的作用,使模型趋于简单。极限情况就是大部分参数值都为0。
还有一种理解就是,比如使用tanh作为激活函数,参数值w减小会使z值减小,此时tanh函数近似于一个线性函数,同样使模型变得简单。
另一种正则化方法就是Dropout,这种方法随机使一部分神经元失活来增强网络。常用的实现方法就是“反向随机失活”(Inverted dropout),以第三层为例:
keep_prop = 0.8 d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prop a3 = np.multiply(a3, d3) a3 /= keep_prop
其中keep_prop是神经元存活的概率,可以看出对于每个样本失活的神经元都不同。
注意:
- 最后要除以keep_prop是为了保持a3的期望值不变,补偿因为神经元失活导致的激活值减小。
- 注意在测试阶段并不使用Dropout。
- Dropout的作用类似于 \( L_2 \) 正则化。直观地理解是,网络不能依赖于任何一个特征,而是要分散风险,这也会导致权重偏小。
- Dropout主要用在计算机视觉领域中,其他领域很少应用。除非出现过拟合,否则不要使用。
- 可以对不同层设置不同的keep_prop,在参数量过多,更有可能出现过拟合的层应用更小的keep_prop。
其它正则化的方法还有:数据扩增(data augmentation)和早停(early stopping)
对于图片可以通过旋转、水平翻转和裁剪等方法进行数据扩增,这样以较小的代价就可以得到较多数据。
训练过程中同时画出训练集和验证集误差随迭代次数变化的曲线,选择验证集误差的拐点提前停止迭代。
1.9 归一化输入
提升神经网络训练速度的重要方法是归一化输入:
\( \mu = \frac{1}{m} \sum_{i=1}^{m} x^{(i)}, \qquad x = x-\mu \)
\( \sigma^2 = \frac{1}{m} x^{(i)^2}, \qquad x = x / \sigma^2 \)
注意要保持测试集和训练集进行了同样的归一化。
归一化有利于代价函数的优化,如图:
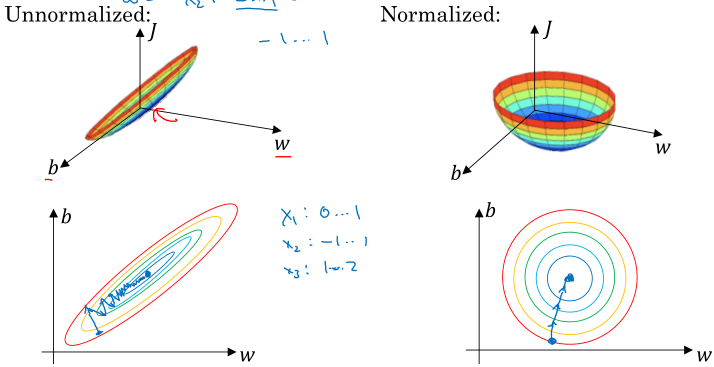
对于特征变量范围差异较大的,归一化很有必要;对于特征变量范围差异较小的,归一化不是必要的,但是做了并没有什么坏处。
1.10 & 1.11 梯度消失与梯度爆炸
这在深度学习中也是一个比较著名的问题,即 \( 0.9^n \) 和 \( 1.1^n \) 。梯度和变量的值都是随着网络深度指数级增长或减小,导致代价函数难以优化。
吴恩达老师给出了一种解决方法,就是初始化权重时采取:
\( W^{[l]} = \text{np.random.randn(W.shape)} * \text{np.sqrt} ( \frac{ 2 }{ n^{[l-1]} } ) \)
可以看到就是根据输入的特征数确定随机参数的方差,直观理解就是越大的 \( n \) 对应越小的 \( w \),相应的激活值既不会太大也不会太小。
1.12 & 1.13 & 1.14 梯度检验
梯度检验就是检查梯度的数值计算结果与推导公式结果是否相一致,目的是保证反向传播的正确。
具体实现时,要将网络所有参数展开组成一个长向量\( \theta \),然后对于向量的每一个分量计算:
\( \begin{gathered} d\tilde{\theta}[i] = \frac{J(\theta_1, \theta_2, \dots, \theta_i +\epsilon, \dots) - J(\theta_1, \theta_2, \dots, \theta_i - \epsilon, \dots)}{2\epsilon} \end{gathered} \)
\( \begin{gathered} d\theta[i] = \frac{\partial J}{\partial \theta_i} \end{gathered} \)
然后通过计算:
\( \begin{gathered} \frac{\| d\tilde{\theta} - d\theta \|_2}{ \| d\tilde{\theta} \|_2 + \| d\theta \|_2 } \end{gathered} \)
判断梯度表达式是否正确,如果在\( 10^{-7} \) 级别甚至更小,那基本没有问题;如果在 \( 10^{-3} \) 级别甚至更大,那么要仔细检查参数向量,可能推导或者程序有问题。
还要注意,梯度检验的开销较大,所以只在调试的时候开启梯度检验,正式训练的时候不再进行;不要漏了正则化项;不要和Dropout一起使用;可以在训练一段时间之后再次进行梯度检验。



