【贪心算法】NO134 加油站
134. 加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2] 输出: 3 解释: 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油 开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油 开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油 开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油 开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。 因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3] 输出: -1 解释: 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。 我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油 开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油 开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油 你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。 因此,无论怎样,你都不可能绕环路行驶一周。
提示:
gas.length == ncost.length == n1 <= n <= 1050 <= gas[i], cost[i] <= 104
暴力超时
public int canCompleteCircuit(int[] gas, int[] cost) { var len = gas.length; var diff = new int[len]; var sum = 0; for (var i = 0; i < len; i++) { diff[i] = gas[i] - cost[i]; sum += diff[i]; } if (sum < 0) { return -1; } for (var i = 0; i < len; i++) { if (diff[i] < 0) { continue; } var j = (i + 1) % len; var count = diff[i]; while (j != i) { count += diff[j]; j = (j + 1) % len; if (count < 0) { break; } } if (j == i) { return i; } } return -1; }
贪心算法解法一:
public int canCompleteCircuit(int[] gas, int[] cost) { var len = gas.length; var sum = 0; var min = Integer.MAX_VALUE; for (var i = 0; i < len; i++) { sum += gas[i] - cost[i]; min = Math.min(min, sum); } //System.out.print(min); if (sum < 0) { return -1; } if(min >= 0) { return 0; } for(var i = len - 1; i >= 0; i--) { min += gas[i] - cost[i]; if(min >= 0) { return i; } } return -1; }
- 首先,从0开始迭代,找出每日剩余(gas[i] - cost[i])的
最小值min和和sum - 如果sum<0则无论从哪个加油站开始都无法遍历全部
- 如果最小值min>=0则证明从0号站出发没有出现断油,返回0
- 否则则最小值为负数,从后
往前查找并累加每日消耗能够填平这个负数的值,返回这个值的下标
为什么是往前查找?min记录的是从0开始到某一下标(假设为i)的消耗总和的最小值,所以想要找能够填平这个负数的下标,需要从0的前面,也就是len-1的位置开始,不断向前累加,直到出现大于等于零的下标。
min区间后是不会出现负数的,因为如果后面出现负数的话,min就会得到更新从而变得更小
贪心算法解法二:
public int canCompleteCircuit(int[] gas, int[] cost) { var len = gas.length; var curSum = 0; var totalSum = 0; var ans = 0; for (var i = 0; i < len; i++) { curSum += gas[i] - cost[i]; totalSum += gas[i] - cost[i]; if(curSum < 0) { ans = i + 1; curSum = 0; } } //System.out.print(min); if (totalSum < 0) { return -1; } return ans; }
算法核心思想:
如果当前从0到i的累加和curSum小于零,则说明从0到i的下标均不能作为开始加油站下标,那么就让i+1尝试作为初始下标,并重置curSum为0.验证贪心算法的正确性最好的就是列举一些反例:
-
i+1后会不会出现更大的负数?和前面一样,如果出现再使curSum小于0的话,就会又更新为i+1了
-
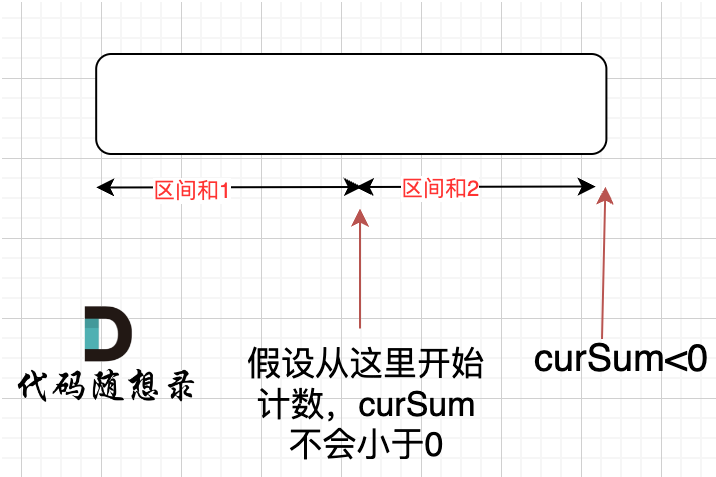
如果[0, i]区间选某一个中间点作为起点到i,累加到curSum是不小于零呢?
不会的,如下图:按照上面的假设,总体curSum<0即 区间和1 + 区间和2 < 0,而区间和2>0,那么区间和1 < 0,这是不可能的,如果区间和1小于零,意味着早就该更新curSum为0了
分类:
数据结构与算法 / 贪心
, 数据结构与算法





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步