Codeforces 938 D. Buy a Ticket

D. Buy a Ticket

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Musicians of a popular band "Flayer" have announced that they are going to "make their exit" with a world tour. Of course, they will visit Berland as well.

There are n cities in Berland. People can travel between cities using two-directional train routes; there are exactly m routes, i-th route can be used to go from city v_i to city u_i (and from u_i to v_i), and it costs w_i coins to use this route.

Each city will be visited by "Flayer", and the cost of the concert ticket in i-th city is a_i coins.

You have friends in every city of Berland, and they, knowing about your programming skills, asked you to calculate the minimum possible number of coins they have to pay to visit the concert. For every city i you have to compute the minimum number of coins a person from city i has to spend to travel to some city j (or possibly stay in city i), attend a concert there, and return to city i (if j ≠ i).

Formally, for every 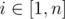you have to calculate 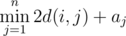, where d(i, j) is the minimum number of coins you have to spend to travel from city i to city j. If there is no way to reach city j from city i, then we consider d(i, j) to be infinitely large.

Input

The first line contains two integers n and m (2 ≤ n ≤ 2·10⁵, 1 ≤ m ≤ 2·10⁵).

Then m lines follow, i-th contains three integers v_i, u_i and w_i (1 ≤ v_i, u_i ≤ n, v_i ≠ u_i, 1 ≤ w_i ≤ 10¹²) denoting i-th train route. There are no multiple train routes connecting the same pair of cities, that is, for each (v, u) neither extra (v, u) nor (u, v) present in input.

The next line contains n integers a₁, a₂, ... a_k (1 ≤ a_i ≤ 10¹²) — price to attend the concert in i-th city.

Output

Print n integers. i-th of them must be equal to the minimum number of coins a person from city i has to spend to travel to some city j (or possibly stay in city i), attend a concert there, and return to city i (if j ≠ i).

Examples

Input

4 2
1 2 4
2 3 7
6 20 1 25

Output

6 14 1 25 

Input

3 3
1 2 1
2 3 1
1 3 1
30 10 20

Output

12 10 12 

 

【题意】

给$$$n$$$个城市，$$$m$$$条无向边，以及所有的点权$$$a_i$$$，边权$$$w_{(i,j)}$$$，对每个结点$$$i$$$，求一个结点$$$j$$$，使得$$$2*d(i,j)+a_j$$$最小 -d(i,j)表示i到j的一条最短路径的花费

【思路】

可以这样理解点权：假想所有结点再走$$$a_i$$$可以到达一个最终点，把点权转化为这个结点到最终点的这条边的边权。再来看$$$2*d(i,j)+a_j$$$，如果抽象地看，把$$$2*d(i,j)$$$当做$$$i$$$到$$$j$$$的距离，而$$$a_j$$$是j到最终点的距离，就赋予了新的含义，要求的值可以看作从$$$i$$$到最终点的最短路，于是问题就转化为了单源最短路问题，用Dijkstra可以求解。

【注意】

为了方便Dijkstra的求解，可以预先把输入的边权直接翻倍

【代码】

#include<stdio.h>
#include<vector>
using std::vector;
#include<queue>
#include <functional>
using std::priority_queue;
using std::greater;
using std::pair;
using std::make_pair;
typedef long long LL;
#define N_max 200005
#define  mp(x,y) make_pair(x,y)

typedef pair<LL, int> PLi;
vector<PLi> node[N_max];

LL dis[N_max];
int vis[N_max] = { 0 };
int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    int fr, to;
    LL val;
    for (int i = 0; i < m; ++i) {
        scanf("%d %d %lld", &fr, &to, &val);
        node[fr].push_back(mp(2*val, to));
        node[to].push_back(mp(2*val, fr));
    }
    for (int i = 1; i <= n; ++i) {
        scanf("%lld", &val);
        dis[i] = val;
    }
    priority_queue<PLi,vector<PLi>,greater<PLi>> help;
    for (int i = 1; i <= n; i++) 
        help.push(mp(dis[i], i));
    while (!help.empty())
    {
        PLi    cur = help.top(); help.pop();
        if (vis[cur.second] == 1)continue;
        vis[cur.second] = 1;

            int nadd = cur.second;
            int sz = node[nadd].size();
            for (int i = 0; i < sz; ++i) {
                PLi next = node[nadd][i];
                if (dis[nadd] + next.first < dis[next.second]) {
                    dis[next.second] = dis[nadd] + next.first;
                    help.push(mp(dis[next.second], next.second));
                }
            }
    }
    for (int i = 1; i <= n; i++)
        printf("%lld ", dis[i]);
    return 0;
}