4.K均值算法--应用
1. 应用K-means算法进行图片压缩
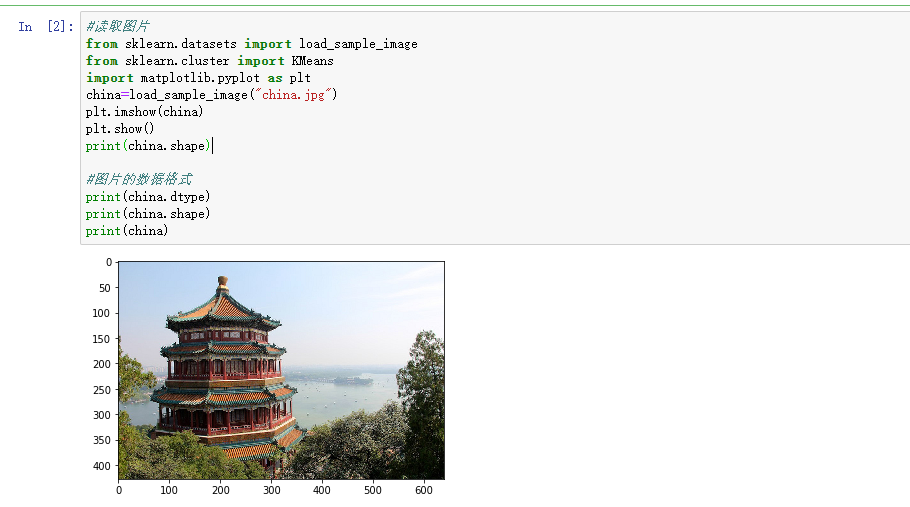
读取一张图片
观察图片文件大小,占内存大小,图片数据结构,线性化
用kmeans对图片像素颜色进行聚类
获取每个像素的颜色类别,每个类别的颜色
压缩图片生成:以聚类中收替代原像素颜色,还原为二维
观察压缩图片的文件大小,占内存大小
#读取图片 from sklearn.datasets import load_sample_image from sklearn.cluster import KMeans import matplotlib.pyplot as plt china=load_sample_image("china.jpg") plt.imshow(china) plt.show() print(china.shape) #图片的数据格式 print(china.dtype) print(china.shape) print(china)
#导入处理图片和绘制图片的库 from sklearn.datasets import load_sample_image from sklearn.cluster import KMeans import matplotlib.pyplot as plt import numpy as np #图片处理前 china=load_sample_image('china.jpg') plt.imshow(china) plt.show() image=china[::3,::3] image.shape plt.imshow(image) plt.show() #把二维的变成线性的 x=image.reshape(-1,3) #图片处理后 #255*255*255 model=KMeans(n_clusters=64) #一维数组 b=model.fit_predict(x) #二维(64,3) a=model.cluster_centers_ a[b]

观察占用内存的大小
import sys sys.getsizeof(china)

sys.getsizeof(image)

import matplotlib.image as img img.imsave('D://zzj-01.jpg',china) img.imsave('D://zzj-02.jpg',image)
观察文件的大小

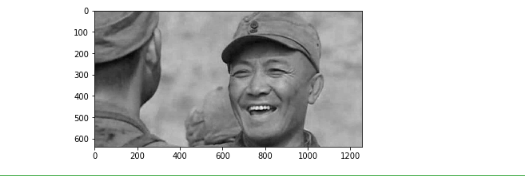
在生活中K均值的实际应用是实现彩色图片和黑白图片的转化。
#准备处理的图片
import matplotlib.image as img
S=img.imread('d:\\zzj083.jpeg')
plt.imshow(S)
plt.show()
#查看图片的数据特点
print (S.shape)
S

#把图像变为黑白
plt.imshow(S[:,:,0],plt.cm.gray)
plt.show()
2. 观察学习与生活中可以用K均值解决的问题。
从数据-模型训练-测试-预测完整地完成一个应用案例。
这个案例会作为课程成果之一,单独进行评分。
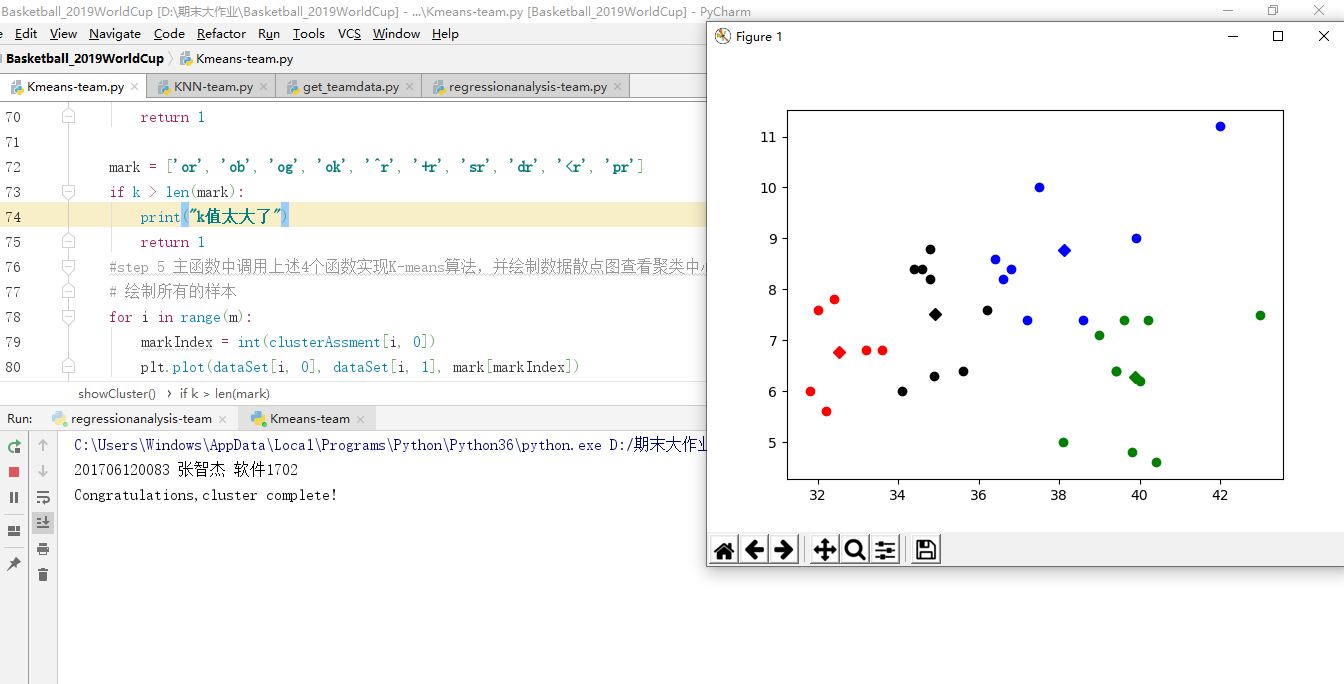
K-means算法,也称为K-平均或者K-均值,一般作为掌握聚类算法的第一个算法。这里的K为常数,需事先设定,通俗地说该算法是将没有标注的 M 个样本通过迭代的方式聚集成K个簇。在对样本进行聚集的过程往往是以样本之间的距离作为指标来划分。该算法读取预处理过的TXT文件,引用三分球命中率和篮板球的数据,将k值设为4,绘出有四个质点的散点图,可以看出这组数据的聚集程度。具体代码如下:
print("201706120083 张智杰 软件1702") import numpy as np import matplotlib.pyplot as plt # step 1 加载数据 def loadDataSet(fileName): data = np.loadtxt(fileName, delimiter='\t') return data # step 2 欧氏距离计算 def distEclud(x, y): return np.sqrt(np.sum((x - y) ** 2)) # 计算欧氏距离 # step 3 构建k个随机质心 def randCent(dataSet, k): m, n = dataSet.shape centroids = np.zeros((k, n)) for i in range(k): index = int(np.random.uniform(0, m)) # centroids[i, :] = dataSet[index, :] return centroids # step 4 K-means函数实现算法。 def KMeans(dataSet, k): m = np.shape(dataSet)[0] # 行的数目 # 第一列存样本属于哪一簇 # 第二列存样本的到簇的中心点的误差 clusterAssment = np.mat(np.zeros((m, 2))) clusterChange = True # 初始化centroids centroids = randCent(dataSet, k) while clusterChange: clusterChange = False # 遍历所有的样本(行数) for i in range(m): minDist = 100000.0 minIndex = -1 # 遍历所有的质心 #找出最近的质心 for j in range(k): # 计算该样本到质心的欧式距离 distance = distEclud(centroids[j, :], dataSet[i, :]) if distance < minDist: minDist = distance minIndex = j # 更新每一行样本所属的簇 if clusterAssment[i, 0] != minIndex: clusterChange = True clusterAssment[i, :] = minIndex, minDist ** 2 # 更新质心 for j in range(k): pointsInCluster = dataSet[np.nonzero(clusterAssment[:, 0].A == j)[0]] # 获取簇类所有的点 centroids[j, :] = np.mean(pointsInCluster, axis=0) # 对矩阵的行求均值 print("Congratulations,cluster complete!") return centroids, clusterAssment def showCluster(dataSet, k, centroids, clusterAssment): m, n = dataSet.shape if n != 2: print("数据不是二维的") return 1 mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr'] if k > len(mark): print("k值太大了") return 1 #step 5 主函数中调用上述4个函数实现K-means算法,并绘制数据散点图查看聚类中心 # 绘制所有的样本 for i in range(m): markIndex = int(clusterAssment[i, 0]) plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex]) mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb'] # 绘制质心 for i in range(k): plt.plot(centroids[i, 0], centroids[i, 1], mark[i]) plt.show() dataSet = loadDataSet('201706120083张智杰.txt') k = 4 centroids, clusterAssment = KMeans(dataSet, k) showCluster(dataSet, k, centroids, clusterAssment)