(科普) 颜色

Color Matching Function 的确立

人眼的实质不是光谱仪而是色度计，对颜色的感知是由三种锥细胞的感受所合成的。人视觉谱中每个波长的光对视锥细胞的刺激能力记为L(lambda),M(lambda),S(lambda),分别对应LMS三种视锥细胞。
这样，我们被给定一个光谱 P(lambda)，我们可以构造出一个三通道色彩表示 (P.L,P.M,P.S)，其中 . 表示点积(连续函数的点积被定义为 a.b=\(\int_R a(x)b(x)\mathrm{d}x\)). LMS三个的刺激值长这样：

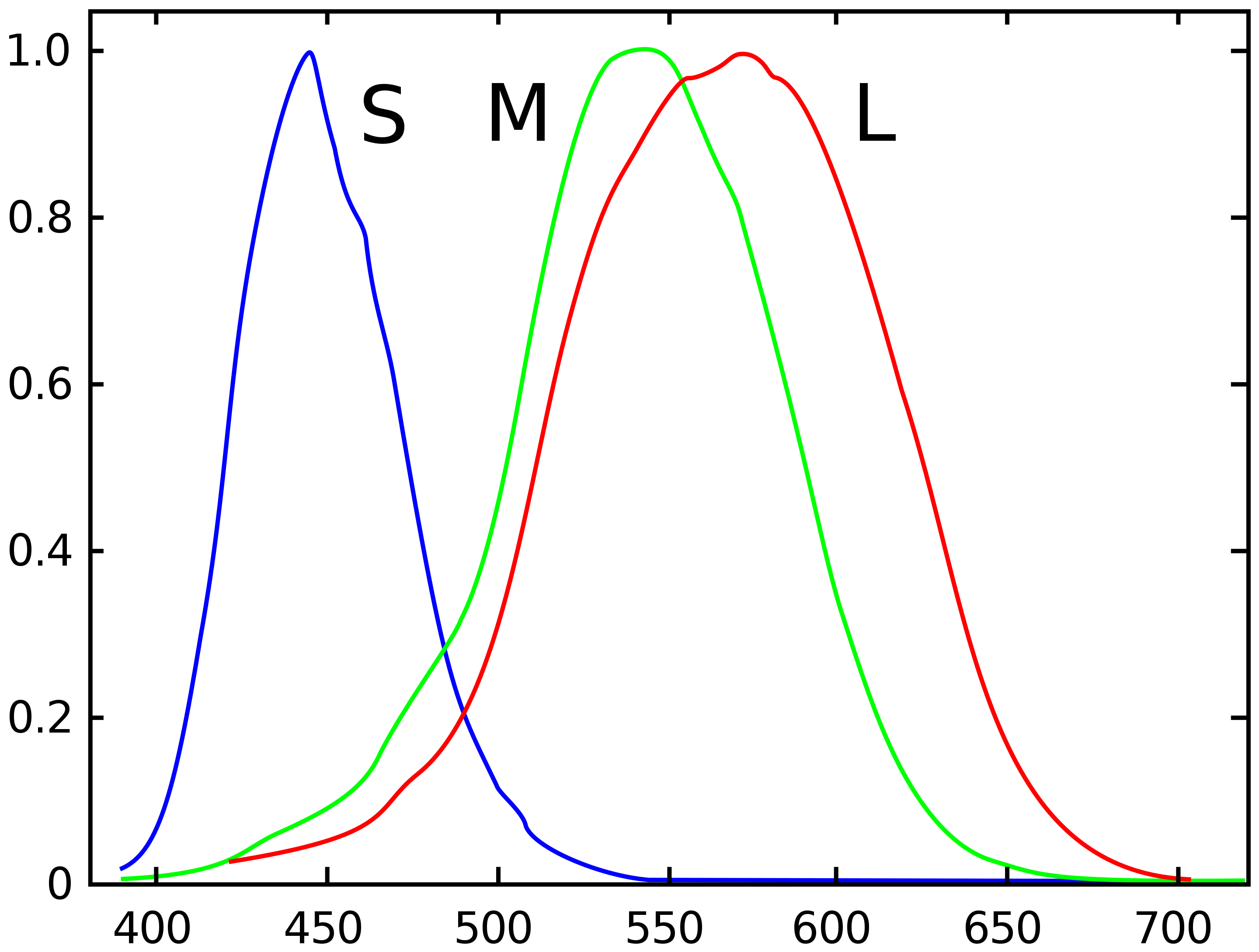
至于这些值是如何计算出来的并不是很关键。

CIE XYZ 是从 Wright-Guild Experiment 的数据中导出的色彩表示。事实上，XYZ 三个分量是 LMS 的线性组合（基于颜色线性混合的事实，这是一定的）。XYZ 的确定比 LMS 更简单，因为它并不涉及细胞本身刺激值的确定。

确定了 XYZ 的是 Wright-Guild 实验，大体上是这样的：

每个观察者被给定了一个颜色，然后试图调整三种标准色的混合色来匹配这个颜色。这三种标准色有时并不能混合出这个颜色，在这时可以对指定色混合上这三种标准色来达到。

C + na R + nb G + nc B = a R + a G + a B

然后这时我们就有 C = (a-na)R+(b-nb)G+(c-nc)B，这些 n 值的出现是为了表示无法存在的负亮度光。选定 C 为固定亮度某一波长的光，我们便可以对所有波长求出其 RGB 刺激值 R(lambda)=a-na, etc.

CIE RGB(1931) 选定了 R=700nm, G=546.1nm, B=435.8 nm 的三色基。以此确定的是 CIE1931 RGB Color Matching Function.

下图是三个波长在 xy 平面上的位置。在这三个波长围成的三角形内的颜色是可以被这三种波长的光混合出来的。

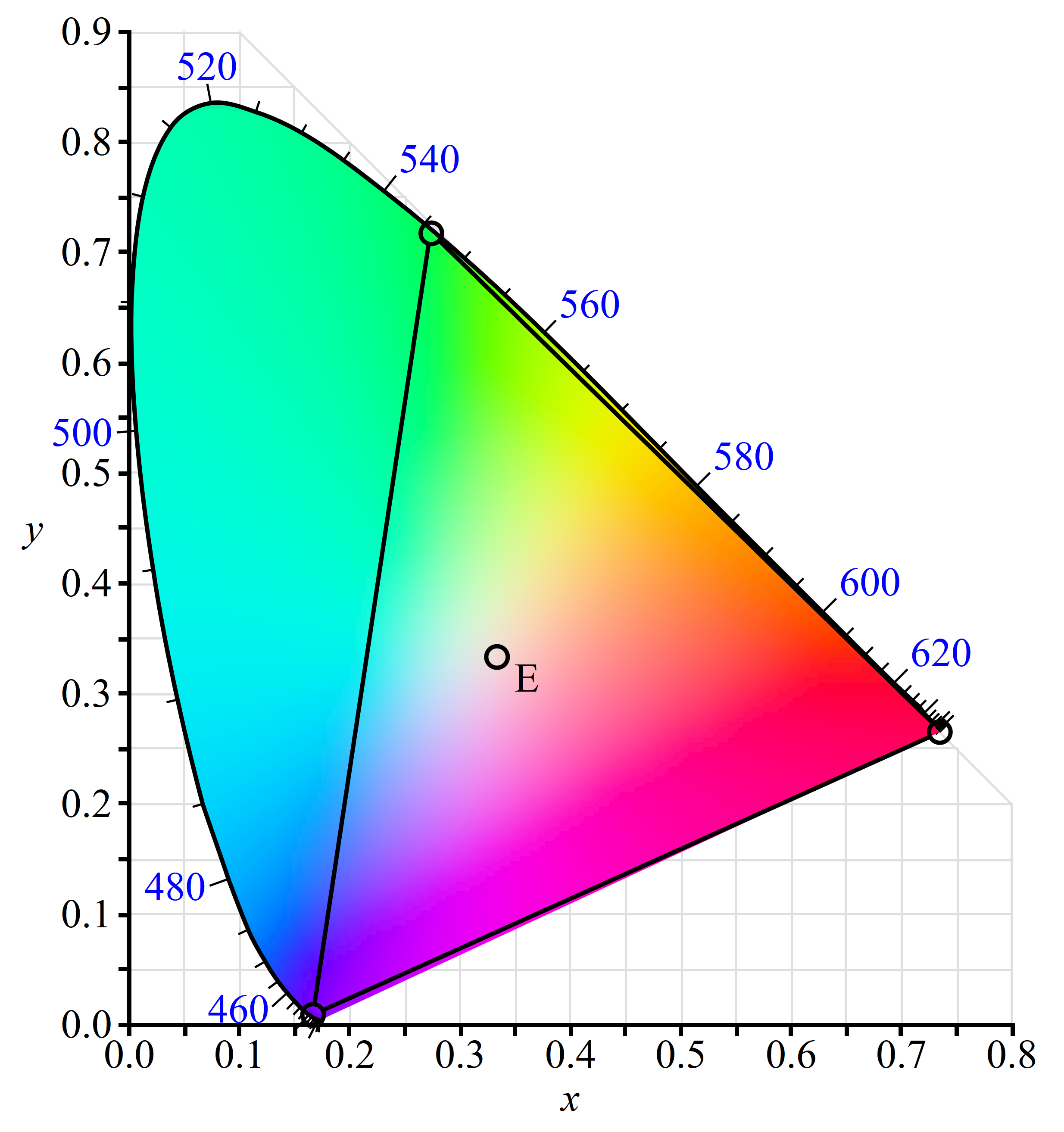
下图是 CIE1931 RGB Color Matching Function. 注意 R, G 都是有负值部分的. 这个负值部分就是靠 na 这些值算出来的.

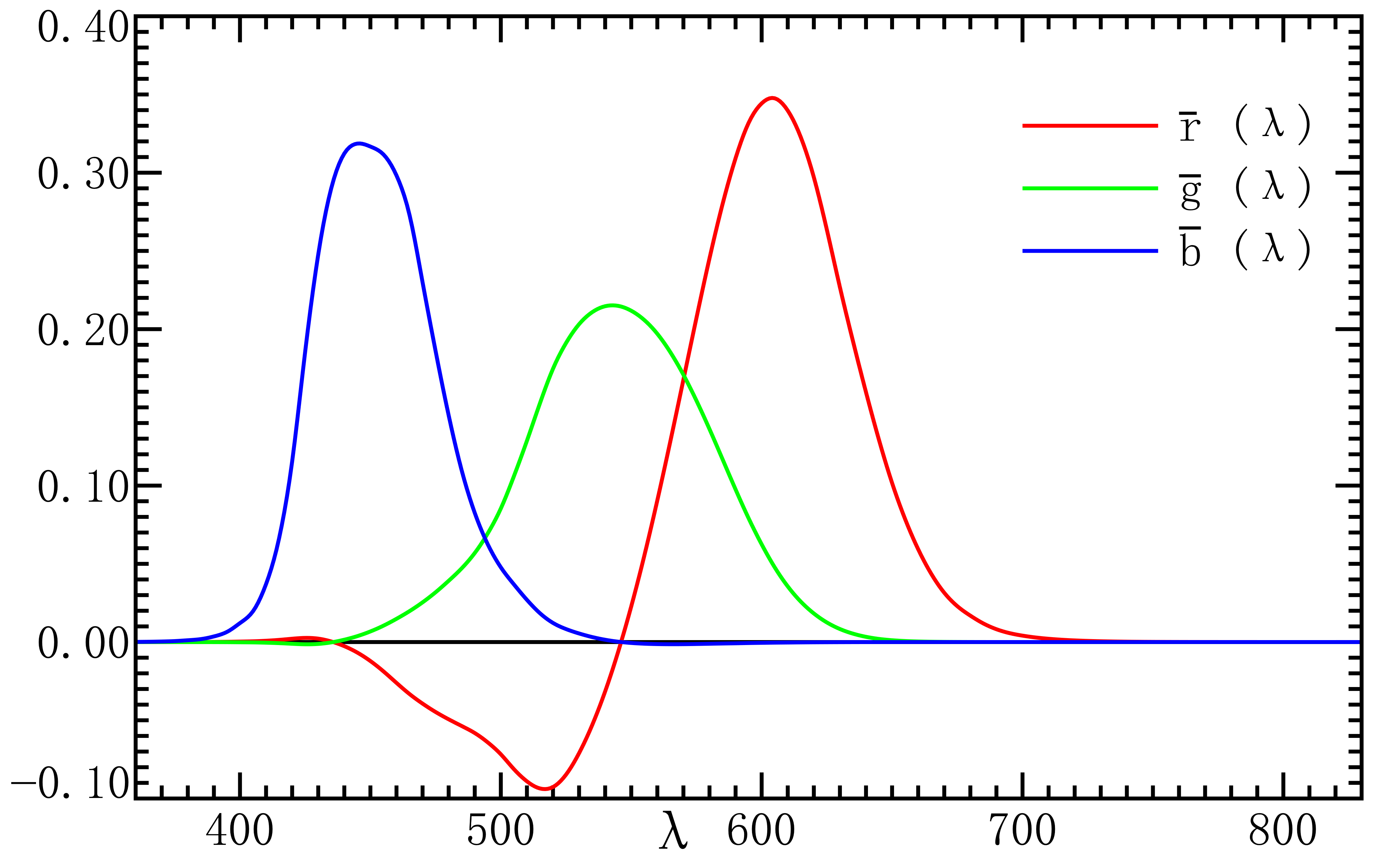
CIE XYZ

由于有负值的使用不便（同时也令人难以接受），对 RGB 基做线性变换获得了 XYZ 基，其中 Y 基被确定为接近视觉亮度的一个分量。

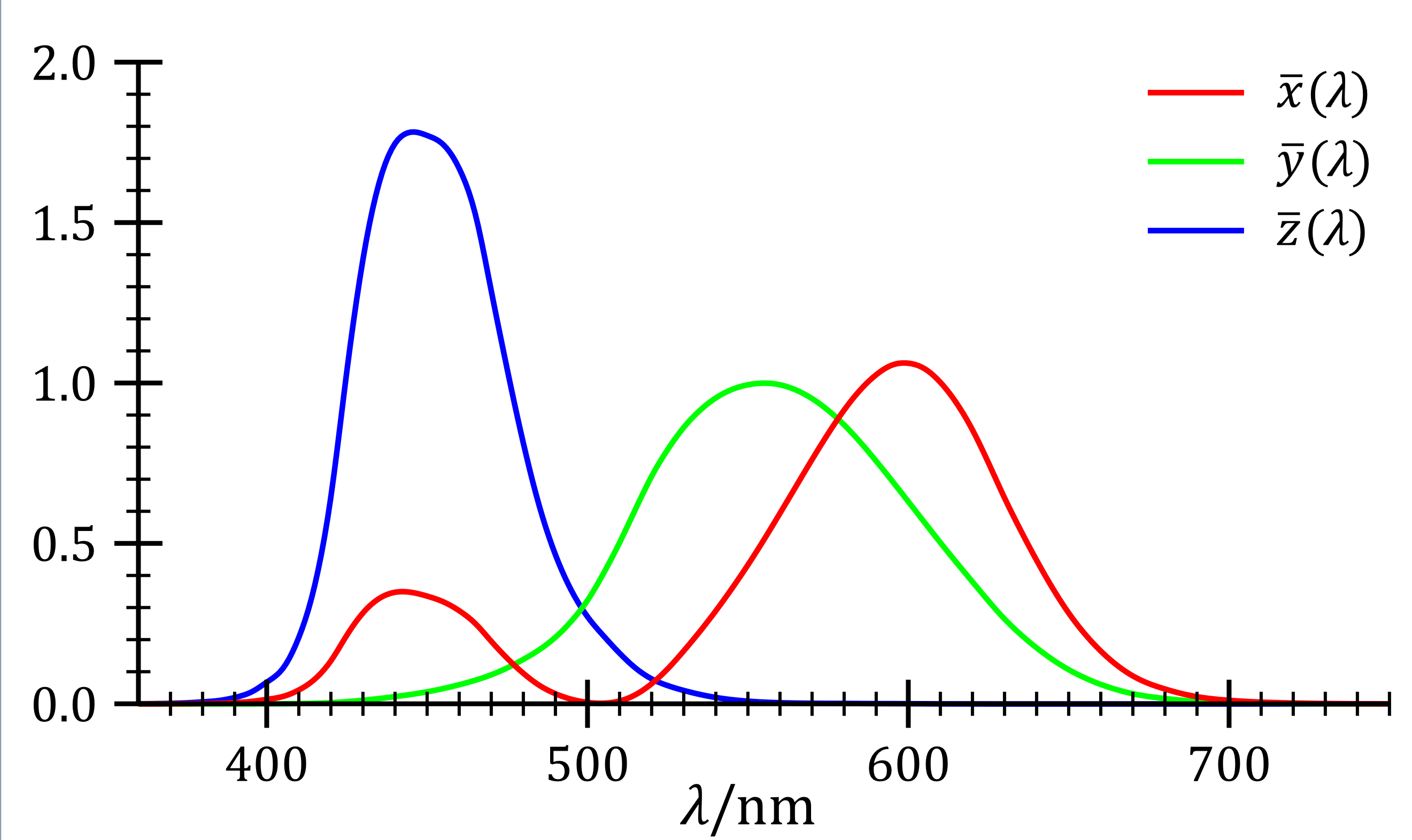
注意到 XYZ 和 LMS 是有区别的。

CIE RGB 对 CIE XYZ 的转换是：

\[\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} = \frac{1}{b_{21}} \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix} = \frac{1}{0.176\,97} \begin{bmatrix} 0.490\,00 & 0.310\,00 & 0.200\,00 \\ 0.176\,97 & 0.812\,40 & 0.010\,63 \\ 0.000\,00 & 0.010\,00 & 0.990\,00 \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix} \]

CIE XYZ 到 CIE RGB 则乘逆矩阵即可。

将 Y 作为亮度分量(luminance)单独提出，构造出了 CIE xyY 色彩空间，xy 两个值专门表示颜色。

\[D=X+Y+Z\\ x=X/D\\ y=Y/D\\ Y=Y \]

这样，就有了经常看到的 xy 坐标的颜色图了。注意，xyY 色彩空间并非线性空间。

CIE L*a*b*

CIE L*a*b* (简称 CIELAB)是为了解决 xy 座标系色彩变化不均匀而产生的色彩空间。同时，CIELAB 是一个考虑了白平衡的色彩空间。

CIEXYZ 到 CIELAB 的转换是：

\[{\displaystyle {\begin{aligned}L^{\star }&=116\ f\!\left({\frac {Y}{Y_{\mathrm {n} }}}\right)-16\\a^{\star }&=500\left(f\!\left({\frac {X}{X_{\mathrm {n} }}}\right)-f\!\left({\frac {Y}{Y_{\mathrm {n} }}}\right)\right)\\b^{\star }&=200\left(f\!\left({\frac {Y}{Y_{\mathrm {n} }}}\right)-f\!\left({\frac {Z}{Z_{\mathrm {n} }}}\right)\right)\end{aligned}}}\\ {\displaystyle {\begin{aligned}f(t)&={\begin{cases}{\sqrt[{3}]{t}}&{\text{if }}t>\delta ^{3}\\{\frac {t}{3\delta ^{2}}}+{\frac {4}{29}}&{\text{otherwise}}\end{cases}}\\\delta &={\frac {6}{29}}\end{aligned}}} \]

其中，\(X_n, Y_n, Z_n\) 是标准白点的三个分量值，比如 D65: \((X_n,Y_n,Z_n)=(95.048\,9,100,108.884\,0)\)，这里，需要将 \(Y_n\) 标准化至 100.

（继续借维基的图）

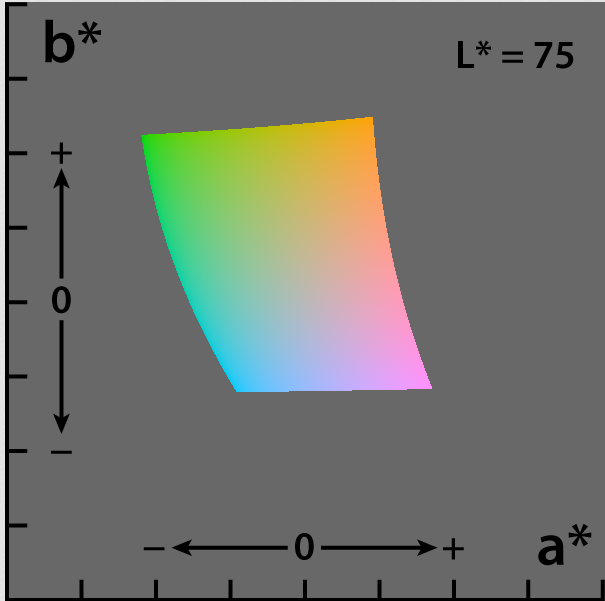
可以看到它的色彩变化很平滑。

其它色彩空间

其它色彩空间就可以基于这些定义了。对于加性色彩空间（比如各种 RGB），重要的参数是基色和 Tone Curve。白点可以通过基计算出来。

比如说 sRGB: 三个基色是(CIE xyY表示) R(0.64,0.33,0.2126) G(0.3,0.6,0.7152) B(0.15,0.06,0.0722). 三个 Y 值的和是 1，三个 X 值的和是 0.9504，etc. 因此 sRGB 的白点是 D65@Y=1: (0.9505,1,1.0890).

有一个常见的误区，是由于平时看的图只有 xy 轴没有 Y 轴造成的：就是色彩空间的白点脱离 RGB 存在。事实上 W=R+G+B。但是反过来说，如果只给定 R,G,B,W 的 x,y 值，是可以计算出色彩空间的（假定W的Y=1），这样的情况下，事实上我们可以创造出和 sRGB 色域相同而白点不同的平行色彩空间，这是有用的，比如在白平衡的调整上（虽然更建议通过CIELAB调整）。

Tone Curve 是另一个重要特性：为了不浪费数值精度，让明暗变化更接近视觉，需要使用 Tone Curve. 比如 sRGB 的 Tone Curve 是（ XYZ(线性值) 到 sRGB 的变化）:

\[{\displaystyle \gamma (u)={\begin{cases}12.92u&u\leq 0.0031308\\1.055u^{1/2.4}-0.055&{\text{otherwise}}\end{cases}}} \]

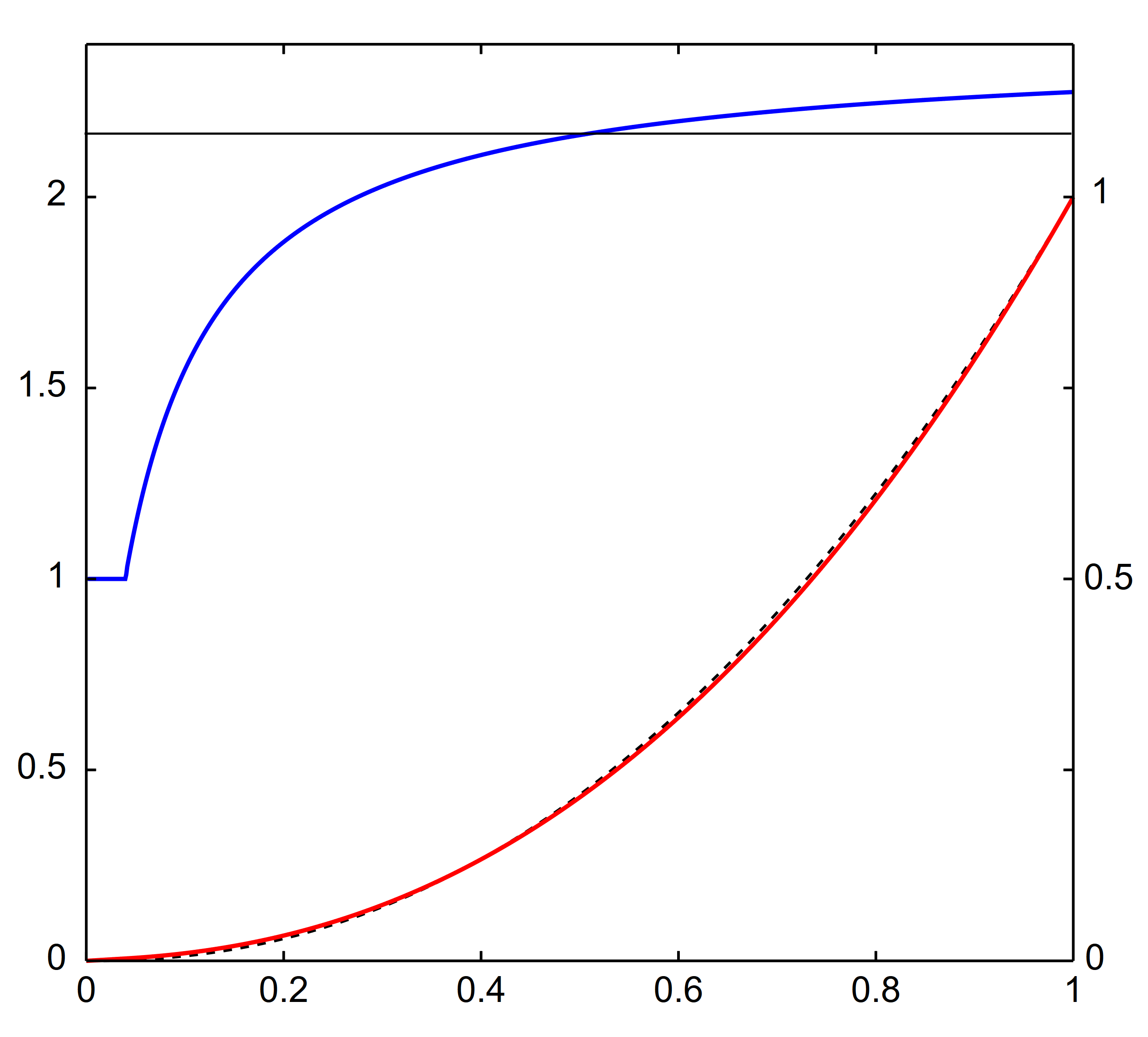
这个 Tone Curve 这么奇怪，其实是有意图的：sRGB 逼近的是 Gamma=2.2 的曲线，在接近 0 的地方使用线性函数近似以规避精度问题(因为导数会趋向正无穷)。

（注意下图是 sRGB 值到 XYZ(线性) 值的曲线，是上面那个的反函数）